確率分布・標本からの統計的推測をStataで計算してみる | 医療統計とStataプログラミングの部屋

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています．ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて、今回も前回に引き続き統計バリバリで行きますが、特に今回は初歩中の初歩である、連続した値がとる範囲における確率についてまとめてみました．

1．確率変数・確率分布
2．確率分布が正規分布に従うとき
3．標本抽出して全体を推し量る
まとめ

1．確率変数・確率分布

はじめに用語の整理をしましょう．

確率変数(random variable)：ある試行によって取りうる値のこと（例：サイコロなら｛1,2,3,4,5,6｝）→　ある試行によって取りうる値を変数Xで表したときそのXが確率変数．
確率分布(probability distribution)：確率変数Xの取りうる値とそれらの確率との対応関係のこと

特にコインの表裏、サイコロの目のように飛び飛びの値をとる確率変数のことを離散型確率変数といい、その確率分布を確率関数と言います．

飛び飛びの値をとらずに連続した値をとるときは連続型確率変数といい、このとき確率分布を表現するために確率密度関数(probability density function) f(X)を用います．

離散型・連続型のどちらの確率変数に対しても、累積分布関数あるいは分布関数 F(X) がありますが、連続型についてはこのF(X)を微分すると確率密度関数f(X)になります．

確率密度関数の曲線下面積はすべての事象となるので1になります．

連続型確率変数の確率分布には、正規分布、χ2分布、F分布、t分布などがあります．今回は正規分布とt分布のstatisticsについて、Stataを使って計算してみましょう．

2．確率分布が正規分布に従うとき

量的変数の分析で最も頻繁に出現する、連続型確率分布の代表格が正規分布です．

式で表すと以下のようにややこしいのですが、これは覚える必要はありません．

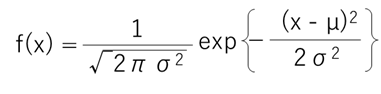
簡単に、正規分布 N(µ, σ²)と書き表したりします．

平均µを中心に左右対称で、±σのところで変曲点を持ち、0.683の確率でこの幅に収まる特徴があります．

そして、期待値0、分散1のときの正規分布N(0,1）を標準正規分布と言います．

stataで標準正規分布のヒストグラムを描く場合には、正規分布する乱数を発生させましょう．

1000 observationをもつデータセットを作り出して、そこに乱数を発生させればできます．

set obs 1000
gen id = _n
gen random=rnormal()
hist random, norm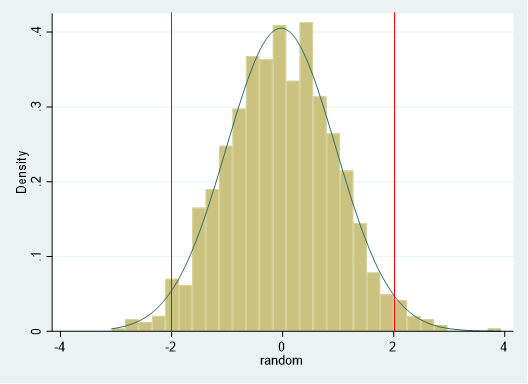

この標準正規分布にすべてそろえるように考えればよいのです．

ある分布において特定の値以上をとるときの確率を問われているとした場合、その値が平均からどの程度逸脱しているのか、それを標準偏差の個数分として表現したZスコアを求めることになります．

例えば、平均22、分散9だとした場合、25以上の値をとる確率は、

Z＝(25ー22)/√9 = 1

となりますので、Z値1以上となる確率を標準正規分布の上側確率の表などから探します．あるいはStataで実施するならば、normprob関数を用いて

display normprob(1)　　/* Z＝１以下となる確率 */
.84134475　　/* これを1から引く */
**あるいは
display 1－normprob(1)

ということで、.15865525となり、求められました.

上の図のように、Z値が‐2から+2までをとる確率を求めるとしたら、

display normprob(2) - normprob(-2)
.95449974

このように求まりました.

逆に、パーセンタイル値を求めたいときなどはこの逆のプロセスが必要になります.その時に使う関数が、invnormとなります.

例えば90％タイルの値をとるときのZ値を求めたい場合、

display invnorm(0.9)
1.2815516
display normprob(1.2815516)
.90000001  /* 元に戻ることも確認できた */

このようにして簡単な関数を使って計算することができます.

3．標本抽出して全体を推し量る

統計学は、研究対象である母集団（条件を満たすすべての人、ということで実質的には理想的な値）の特徴を、母集団の一部から抽出して得られた標本から推定することがその大きな役割です.

これを統計的推測といいます.　よく「サンプリング」とか言ったりしますが、全部を調べることなく全体を推測するためにどのくらいの数のサンプルを調べたらいいのか、というのを見積もったりするのが統計学の本来的な役割です.

ある学校の生徒のテストの集計をしたとします.

このとき、全校生徒すべてがそのテストを受けたとして、そのテストの平均や標準偏差を調べたりすることはその学校の生徒たちの成績を「記述」することのみにフォーカスされています.

一方、その学校が全国の成績の中位くらいにあるからという理由で選ばれたとします．そしてそのテストの目的が、全国の学生の能力の全体像を把握することだとすれば、それは統計的推測を行うことになります.

このようにサンプリングを行った場合、手元にあるデータは標本集団のみのデータとなりますので、得られる値は標本平均と標本分散になります．推測したいのは母集団の母数である母平均・母分散です．

標本平均や標本分散は一つ一つはバラバラの値をとります．しかしこのようなサンプリングが数多くなされると標本平均の分布は、自然と母平均・母分散に近づきます．（実際にはサンプリングは何度も行いませんので、得られるのは1回のサンプリングによって得られた平均と分散になります．）

結論から述べると、標本平均の分布は、平均µ、分散σ²/nで表されます．

そしてさらに、標本平均の分散の平方根をとった値を標準誤差(Standard error: SE)といいます.

信頼区間とは、標本から得られた推定値がある確率でとりうる範囲を指します．ここで多くの人が誤解するのですが、

「たまたま得られた標本から計算された95％信頼区間に母数が含まれる確率が95％である」

これは一見正しそうに見えるのですが、違います．そういう意味ではありません．母数は動かないです．動くのは信頼区間です．

「同じ大きさの標本を100回繰り返し、その都度推定値と95％信頼区間ができる．100個の95％の信頼区間というものができるが、そのうち95個には母数が含まれるが、5個には母数が含まれず、5％の確率で間違った区間を推定してしまう」です.

何回も繰り返す、というところがミソですね．

1．母集団の確率分布が正規分布N(µ, σ2)に従うとき

このとき標本も正規分布になるのですが、母集団の分布がN(µ, σ²)ですが、標本平均の分布はN(µ, σ²/n)に従います.

標本平均X＿を標準化すると、

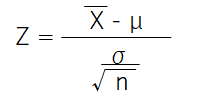
95％信頼区間は、上下合わせて5％の確率となるZ値を標準誤差にかけて範囲を設定します.

disp invnorm(0.975)
1.959964

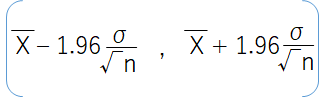
と表されます.

例えば、126サンプルからとった標本平均が29.2、標本分散が7.5²のとき、95％信頼区間はStataでは次のように計算されます．

**95%CI (normal distribution)
display 29.2 - invnorm(0.975)*7.5/sqrt(126)
       *lower bound
display 29.2 + invnorm(0.975)*7.5/sqrt(126)
        *upper bound

2．母集団の分布が正規分布でない場合

標本サイズが大きいとき（目安30以上）は標本平均の分布は正規分布になるということが、中心極限定理から示されるため、上記とほぼ同じ方法で実施可能です．

3．母集団の分布が正規分布で、母分散が未知の場合　

この場合は標本の大きさによって対応が異なります．

標本が比較的大きい（30以上）ときには標本分散s²をσ²の代わりに使って信頼区間を求めます.

標本が小さいときにもやはり標本分散s²をσ²の代わりに使って信頼区間を求めますが、このとき正規分布ではなく、t分布を使います．

t分布は見た目は正規分布によく似ていますが、正規分布よりも山が低く、自由度（サンプル数－1）に応じてその分布が変化するという性質を持っています．

そして信頼区間は以下のようにあらわすことができます．

Stataで実際に計算するときにはinvt関数を用います．これは上側確率と自由度を指定することが正規分布の場合との違いですが、あとは基本的な作りとしてはよく似ていると思います．

サンプル数25、標本平均50、標本分散12²のとき、自由度は24となり、

** 標準誤差(SEM)を計算
display 12/sqrt(25) 

. 2.4

** 自由度25－1のt分布における上側97.5%となるためのt値を求める
display invt(25-1,0.975) 
. 2.0638986 
     *cutoff value(two-sided) under t distribution
display  50 - invt(25-1,0.975)*12/sqrt(25)
. 45.046643
      *lower bound
display  50 + invt(25-1,0.975)*12/sqrt(25)
. 54.953357
      *upper bound

となりました.

まとめ

確率分布、抽出標本から母集団の推測を行う方法について解説しました．

Stataを使った計算ではうまく関数を使ってやってみましょう．