このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、新年一発目の記事ですが、以前の記事でもご紹介したことがありますが、時系列データのパターンを分類していくという手法である、Group-based trajectory modelingについて詳しく説明したいと思います.
1.縦断データの類型化
縦断的なデータから変化をとらえる方法としては、腎疾患領域だとeGFR 30%, 40%減少だったり、Crの2倍化などが有名です.
こういった手法はわかりやすい反面、情報のロス(もっと多くのポイントのデータを使えたのに2つしか使ってない!)、測定誤差(特に平均値から外れた値はその次に測定した際にはより平均値に近づきやすい:平均への回帰)、脱落・欠測などの問題を抱えています.
もう少し高度なテクニックとして、様々な統計モデルへの当てはめを通じて、観察期間における経時的な変化のパターンとしてとらえる方法があります.
このように、何らかのモデリングを通じて、何らかのパターンを想定することを、潜在軌跡モデリング(latent trajectory modeling)と言います.
(ここで、「潜在」、というのは実際に観測されないグループ分けだからだそうです)
こうした潜在軌跡モデリングには、3つの手法があります.
- Growth curve model:集団全体を1つの平均的な軌跡に集約し、個人個人のばらつきに対してはランダム効果で説明する
- Growth mixture model:異なるいくつかの軌跡を想定し、個人個人のばらつきをランダム効果でも説明する
- Group-based trajectory model:異なるいくつかの軌跡を想定して集団全体をいくつかのグループに分け、個人のばらつきを考慮しない.すべての人をいずれかのグループに属するように分類する.
本日紹介するのはこの3つ目のGroup-based trajectory modeling (GBTM)についてです.
2.Group-based trajectory modelingの正しい方法
このグループ分けを行うための指針のようなものが欲しいと思っていたのですが、Latent trajectory modelに関するフレームワークを示すいい論文がありました.
このフレームワークは8つのステップに分かれています.
- Step 1: 暫定的な数の群を設定する(過去の文献や医学的知識を参考に)
- Step 2: 群の数を最適化する(通常1-7群に分け、Bayesian information criteria (BIC)が最も小さい値をとるものを採用する)
- Step 3: モデル構造を最適化する(ランダム効果を含める話なのでGBTMには直接関係ない?)
- Step 4: モデルの十分性をアセスメントする(下記の3指標を通常用いる)
- APPA (average of maximum posterior probability of assignment)>70% for all classes
- OCC values >5.0
- Relative entropy values > 0.5
- Step 5: グラフ的にアセスメント
- 各群のTrajectoryを1つのグラフにプロットする
- 各群のTrajectoryに95%信頼区間をそれぞれ追加する
- 各群を構成する個人のデータを用いてSpaghetti plotを作成する
- Step 6: さらに追加的なdiscrimination toolを使う
- Step 7: 臨床的解釈とその合理性の確認
- Step 8: 感度分析
この流れにそって実施した研究として、全身性強皮症における肺動脈圧上昇パターンとその背景因子を探索するというものがありました.
基本に忠実にまとめられていて非常に勉強になります.
肺動脈圧の軌跡の同定として、群の数と多項式の次数を絞り込んでおいて、あとはそれを、
- 妥当性(APPA >0.7, OCC >5)
- 適合度(Entropy >0.5, lowest BIC)
- 倹約性(Group composition >3%)
- 解釈可能性
の軸で絞り込んでいくというアプローチをとっています.
3.traj コマンドの使い方
さて、このGroup-base trajectory modelingですが、Stataでも実施可能です.
net from http://www.andrew.cmu.edu/user/bjones/traj
net install traj, forceヘルプ画面の一番上のexampleをみてみます.まずはデータセットを展開します.
use https://www.andrew.cmu.edu/user/bjones/traj/data/montreal_sim.dta, clear
よくわからないが、1人1行のデータがありました.
qcpNNop, qasNNdet, qcpNNbat, age の4種類は時系列データのようで、84, 88, 89, 90, 91, 92, 93と7ポイント記録されています.ageだけは1から7まであり、1と2の間が4空いているので、それぞれの数字に対応するのでしょう、きっと.
traj, var(qcp*op) indep(age*) model(cnorm) min(0) max(10) order(1 3 2)このqcpNNopを縦軸にとり、横軸に年齢をとった時系列プロットを作成するというものですが、orderのところが1,3,2となっていますので、3群に分けるのだと分かります.
それで、縦軸は0から10までとりますよ、ということになります.
modelのオプションにはcensored normalを意味するcnormというのが入ります.
で、これを実行してみると、

グループ1はInterceptとLinearとあり、グループ2はcubicまで、グループ3はquadraticまであるのですが、order(1 3 2)に対応しています.この次元については様々な組み合わせを検討していくことになりますが、下の方にあるBICというのをみて、最も数値が低いものを採用する、というかんじになるとおもいます.
また、ここにはGroup membershipがありますが、そこそこ均等に(30.8%、46.1%、23.0%)ばらけているのでよさそうです.エントロピーも0.7より大きいという結果になっています.
traj, var(qcp*op) indep(age*) model(cnorm) min(0) max(10) order(1 3 2)
trajplot, xtitle(Age) ytitle(Opposition) xlabel(6(1)15) ylabel(0(1)6)で、この結果をPlotしてみると、
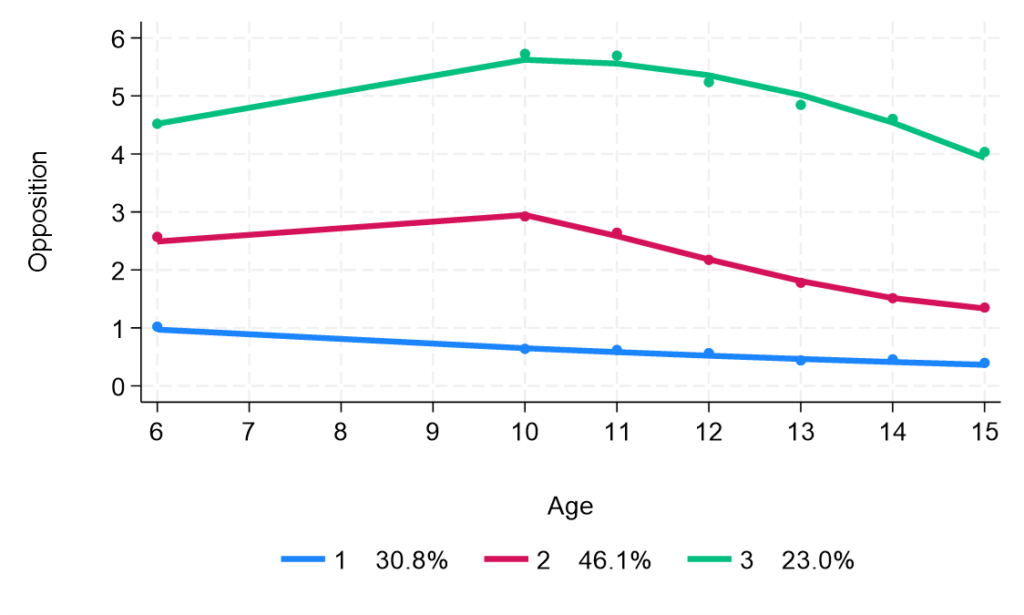
で、妥当性の話はどこにいったの?と思って、このStataプログラムを作った人のページをよく読んでみると、OCCとかAPPAを求めるプログラムを公開しておりました.
program summary_table_procTraj
preserve
*updating code to drop missing assigned observations
drop if missing(_traj_Group)
*now lets look at the average posterior probability
gen Mp = 0
foreach i of varlist _traj_ProbG* {
replace Mp = `i' if `i' > Mp
}
sort _traj_Group
*and the odds of correct classification
by _traj_Group: gen countG = _N
by _traj_Group: egen groupAPP = mean(Mp)
by _traj_Group: gen counter = _n
gen n = groupAPP/(1 - groupAPP)
gen p = countG/ _N
gen d = p/(1-p)
gen occ = n/d
*Estimated proportion for each group
scalar c = 0
gen TotProb = 0
foreach i of varlist _traj_ProbG* {
scalar c = c + 1
quietly summarize `i'
replace TotProb = r(sum)/ _N if _traj_Group == c
}
gen d_pp = TotProb/(1 - TotProb)
gen occ_pp = n/d_pp
*This displays the group number [_traj_~p],
*the count per group (based on the max post prob), [countG]
*the average posterior probability for each group, [groupAPP]
*the odds of correct classification (based on the max post prob group assignment), [occ]
*the odds of correct classification (based on the weighted post. prob), [occ_pp]
*and the observed probability of groups versus the probability [p]
*based on the posterior probabilities [TotProb]
list _traj_Group countG groupAPP occ occ_pp p TotProb if counter == 1
restore
endといれたあとに、summary_table_procTraj と入れてenter!

これでgroupAPPが0.7以上であることがわかりますし、OCCも5を越えています.
ということで、これをセットにしておく必要がありそうです.
4.GBTMの使い道と臨床上の解釈
グループ分けができたら、それをアウトカムとして、ベースライン情報からその軌跡を予測するようなモデルを検討します.
このとき、3群以上に分かれることが多いので、その場合は多項ロジスティック回帰で関連を評価します.
それで、各群に特徴的な背景因子を明らかにすることで、その群の特徴が浮き彫りになるというものです.



コメント