Number needed to be exposed（NNE）とは？

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています． ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて、今回の話題は、Number needed to be exposedについてです．

Number needed to treat（NNT）という指標は、臨床試験における介入効果の尺度としてよく用いられ、リスクやハザード比のような相対的尺度とは対照的に絶対的尺度を提供します．

もうちょっとかみ砕いて説明すると、曝露集団におけるイベント発現割合（リスク）と非曝露集団におけるリスクの比をとったものが相対尺度で、差をとったものが絶対尺度になります（文献）．

各種論文の報告ガイドライン（CONSORT声明やSTROBE声明）では、効果の相対的尺度と絶対的尺度の両方を報告することを推奨していますが、すべての論文でそのような記述があるわけではありません．

意味のある［relevant］場合は，相対リスク［relative risk］を，意味をもつ
期間の絶対リスク［absolute risk］に換算することを考慮する。（STROBE声明）

NNTの概念は臨床試験でより一般的に用いられています．

一方、観察研究では、有害事象に関して曝露された人と曝露されていない人を比較することが一般的であるため、観察研究における同等の指標は通常、曝露必要数（NNE）と呼ばれます（文献）．

有害な曝露と有益な曝露を区別するために、

• あと1人に曝露をもたらしたときの有害性：NNE for one more person to be harmed（NNEH）
• あと1人に曝露をもたらしたときの有益性：NNE for one more person to be benefit（NNEB）

のように区別されます．

この指標をどのように計算し、どのように報告するのが良いか、管理者自身が関わった研究、ならびに知人が発表した研究論文に基づいて徹底解説していきたいと思います．（最近よく聞くフレーズ「徹底解説」使ってみたかっただけ～）

参考にした論文は下記2編です．

• Goto et al. The benefit of reduced serum phosphate levels depends on patient characteristics: a nationwide prospective cohort study. Clin Kidney J. 2024 Oct 4;17(10):sfae263.
• Komaba et al. Lower Parathyroid Hormone Levels are Associated With Reduced Fracture Risk in Japanese Patients on Hemodialysis. Kidney Int Rep. 2024; 9: 2956–2969

いずれも日本透析医学会のデータ解析に基づく論文です．お二人とも超絶優秀な方で、非常に緻密に論文が記載されており、どちらもお手本とさせていただいています．

1．NNE計算の仕方

単純に考えれば曝露群と非曝露群のイベントリスクの差をとって逆数をとる、ということになりますが、調整変数を考慮にいれたイベント発生確率を計算する必要があります．

この場合にはパラメトリックなモデルへの当てはめが最も簡単です．

まずは後藤先生の論文（CKJ）の計算方法からご紹介です．

The 1-year NNEB and NNEH were calculated as follows: first, we estimated the adjusted incident rate ratios (IRR) of outcomes across TA phosphate categories [<3.5, 3.5–<5.0, 5.0–<5.5, 5.5–<6.0, ≥6.0 mg/dL (reference)] using mixed-effects Poisson models. Then, we estimated the difference between predicted probabilities of events per person under the factual (maintaining ≥6.0 mg/dL of TA phosphate levels) and counterfactual (decreasing to 3.5–5.0, 5.0–<5.5 or 5.5–<6.0 mg/dL of TA phosphate levels) scenarios [17]. Finally, 1-year NNEs were calculated by taking the reciprocal of the difference.

1年後のイベントに対するNNEBとNNEHは以下のステップで計算されています．

poisson outcome i.exposurecategory cov1 ocv2, ir

という具合にすれば調整済みのIRRを算出可能ですが、Step 2に関してはどうするのがよいでしょうか？

このステップに関して、Stata journalから素敵な記事があり、引用されていました(17)．

marginal effectを計算する、ということでmarginsコマンドを使用するとよさそうです．

Predict コマンドを使用する場合には、Poisson回帰の場合は以下のようなsyntaxです．デフォルトでは時間当たりのイベント数が算出されます．

それぞれの群における予測確率を求め、リファレンスとの引き算をしたのではないかと思われます．

続いてもう一つの論文(KIR)の方の計算方法です．

We also examined the absolute risk reduction and bootstrapped 95% confidence intervals30 for any fracture and hip fracture associated with >30% reduction in intact PTH over 1 year, and estimated the numberneeded-to-be-exposed31 to >30% reduction in intact PTH to prevent 1 any fracture and 1 hip fracture over 1 year in the overall population and in subgroups of age, sex, and BMI.

こちらは実際にはロジスティック回帰モデルからの算出をしています．

参考にした文献は2002年のBender先生らによる論文（Journal of Clinical Epidemiology 55 (2002) 525–530）になります．

曝露を受けることによるリスク増加は以下の式で求めることができます．

ここで、EER＝exposed event rate、UER＝unexposed event rate のことです．

これらの数値をあらかじめスカラー値として確保しておいて、以下のようなブートストラップのプログラムを作成しました．

program myboot, rclass
syntax [if] [in]
logistic outcome exposure cov1 cov2 cov3 `if' `in'
local or = exp(_b[exposure])
return scalar rr = -(UER*(1 - UER)*(`or'- 1))/(1 + (`or'- 1)*UER)

rr = risk reductionのことです．

多重補完したデータでしたので、これにMIをかませてあげて、10 set分の結果を統合します．

forvalues n = 1/10 {
	preserve
	mi extract `n', clear
	bootstrap r(rr), reps(1000) : myboot
	est store margin_`n'
	restore 
	}
est tab margin_*, b(%7.6f) se(%7.6f)	
mirubin, stub(margin_)

ということで、absolute risk reductionの逆数をとればNNEになりますので、出てきた結果の逆数をとったのですが、信頼区間が0マタギのときに困ったことが起こりました．0の逆数をとらないといけない、という事態に陥ったのです…！

しかし0の逆数は無限大になり計算不能です．ということで表記の仕方に工夫が必要になりました．

2．結果の表現について

算出されたNNEを図式化したものがこちらになります．

①CKJ論文

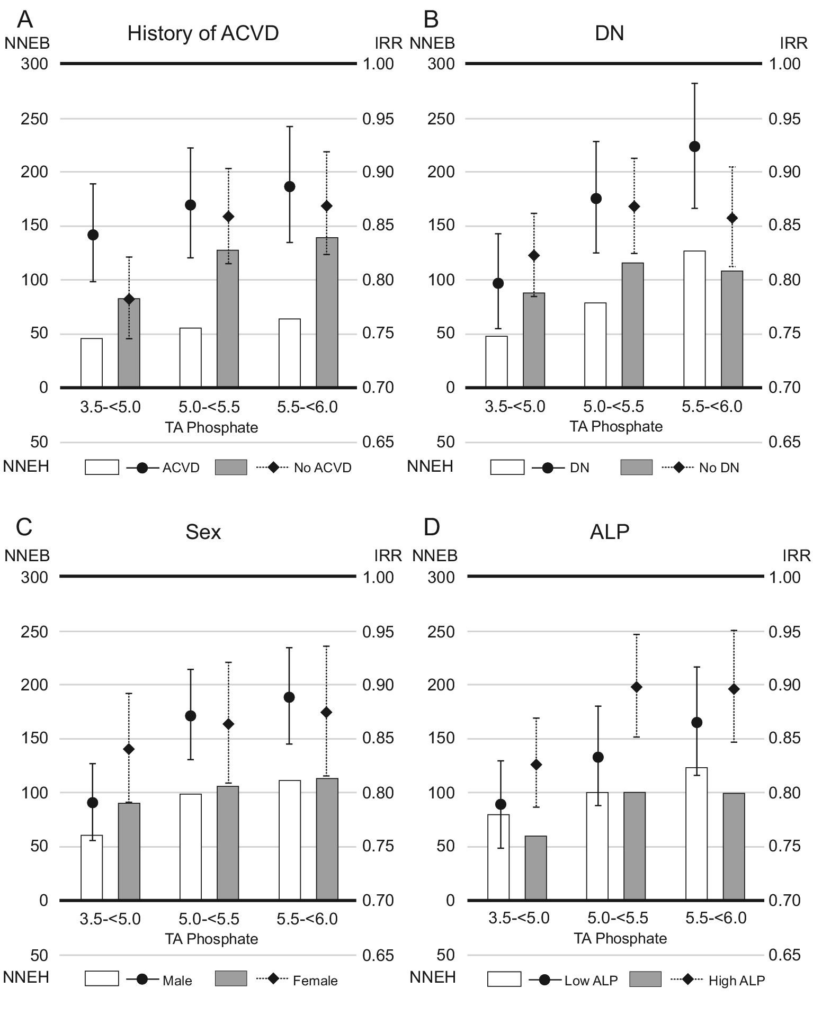
棒グラフでNNEを表現し、フォレストプロットでIRRとその95%信頼区間を表現する、という方法をとっています．NNEについては信頼区間を出していません．

とはいえ理解はしやすいですね．

②KIR論文

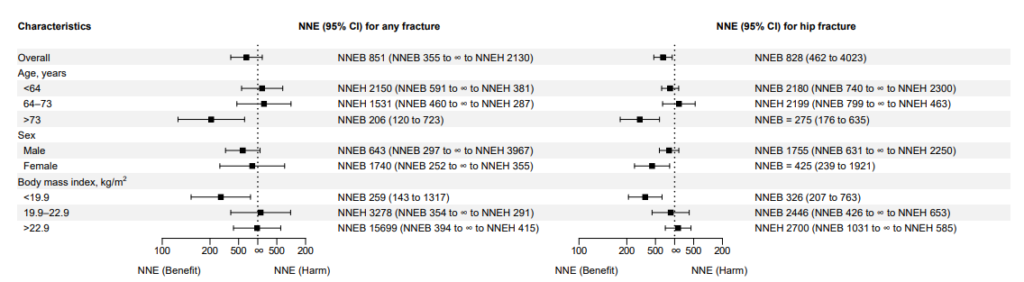
こちらは真ん中に∞を配置して見事に問題解決していました．