臨床予測モデルについて②オプティミズムの求め方

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています． ブログと合わせて個人の学習に役立てて貰えれば幸いです．

ここにアップするために勉強する、というのも変な話ですが、せっかくレンタルサーバー代払っているんだし、有効活用しないといけませんね．実際、記事に纏めるだけでも勉強になっています．

さて、今回は、前回の記事の続編．いよいよ各論に入っていきます．

自分的に聞き覚えがない用語として、optimismという言葉が気になりましたので、それについてまとめてみたいと思います．

予測モデルの作成に関する概要は以前記事にして公開していますが、Internal validationの一環として、「Bootstrap resamplingを行って性能の評価を行う」としていました．

なぜこのようなことをするのかというと、学習データに過度に引っ張られてしまって別の集団にもはや適応できない、というような状況が起こり得ます．これを過剰適合（overfitting）と呼びます．

前回の記事でも紹介していましたね！

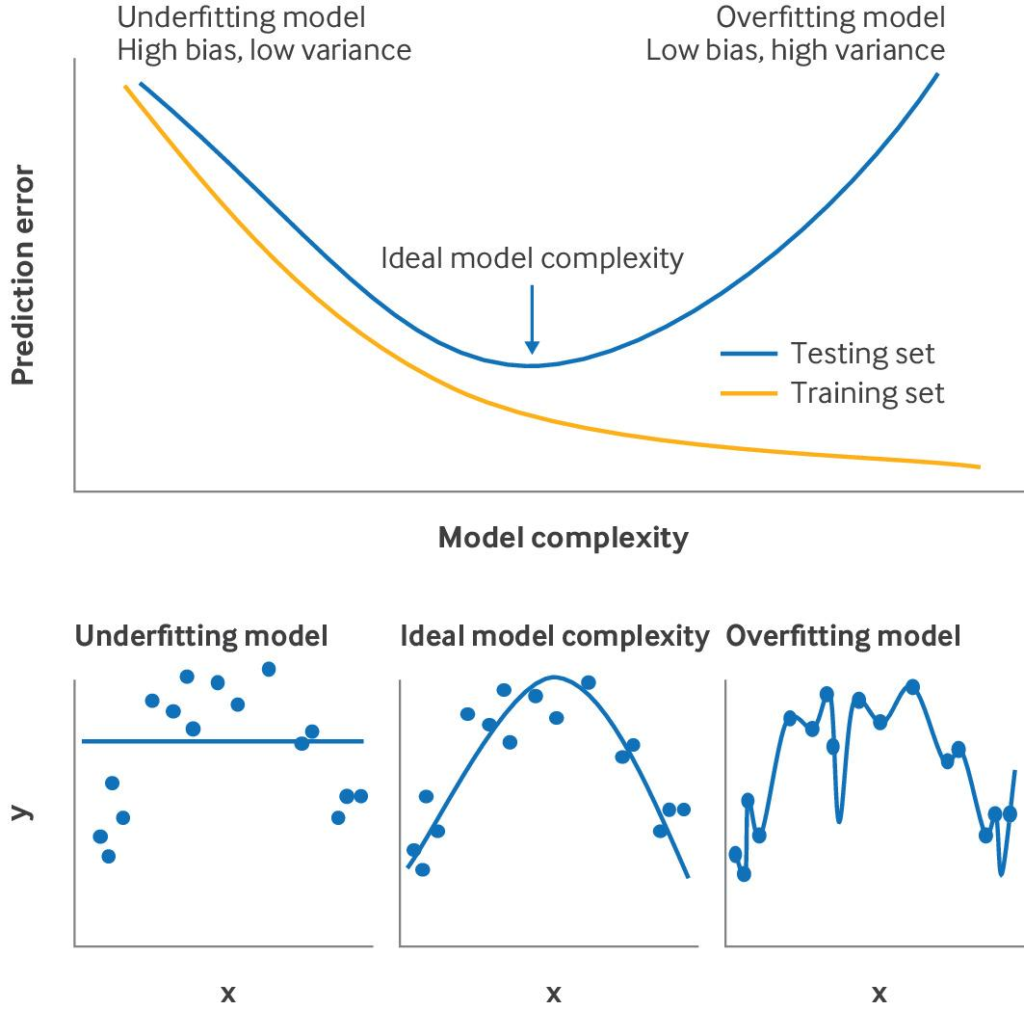
このような過剰適合をしたモデルを”完成品”としてしまうと役立たずなものになってしまうので、元データに「揺さぶりをかける」ようなことをします．これがOptimismの考え方です．

このOptimismを補正してモデル性能を評価し、最適なモデルを選択していく、というのがモデル作成の段階の中に含まれているのです．

Optimismの計算を行うには元の標本からブートストラップ法をもちいた標本再抽出を繰り返し行い、都度性能確認を行ってオリジナルなモデル性能との違いを検証してきます．

ここでおさらいですが、Bootstrapとは何でしょうか？ということで下の図をご参照ください．

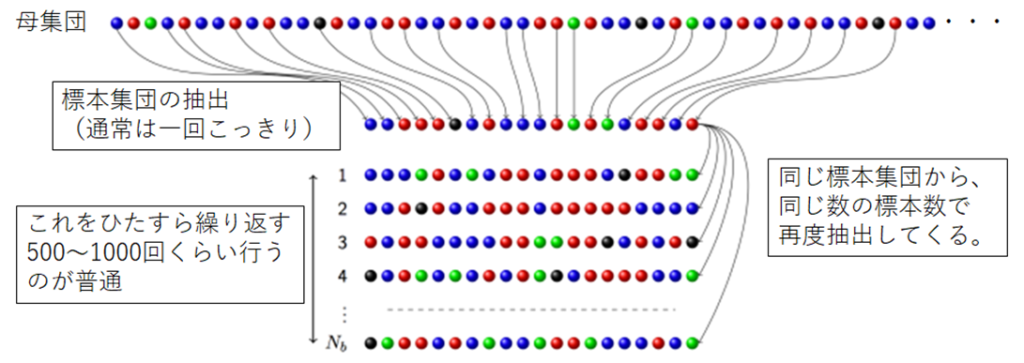
1．オプティミズムの計算手順

オプティミズムの計算の方法は下記の如く、

Optimism ＝ bootstrap性能 – テスト性能

で与えられます．

手順としては以下のように計算していきます．

ちなみにこのポンチ絵はNapkin（https://app.napkin.ai/）というAIツールで作成しました．細かいところの調整はまだあまり上手に指示できないですね～．

2．Stataのプログラムで実装する

Stataでまずは簡単なLogistic regressionをベースにモデルを作成してみましょう．

lbwという、低出生体重のリスクに関するデータベースを用います．

webuse lbw, clear
set seed 20250104

frame create AUCs double(bsa org) int err

tempname bsa
forvalues i = 1/200 {
	preserve
		bsample
		capture logit low age lwt i.race i.smoke ptl ht ui
		if !_rc {
			quietly lroc , nograph
			scalar define `bsa' = r(area)
	restore
			predict double xb, xb
			quietly roctab low xb
			frame post AUCs (`bsa') (r(area)) (0)
			drop xb
		}
		else {
			frame post AUCs (.) (.) (_rc)
			restore
		}
}

cwf AUCs
tabulate err, missing 

quietly generate double delta = bsa - org
summarize delta, meanonly
tempname optimism
scalar define `optimism' = r(mean)

cwf default
quietly logit low age lwt i.race i.smoke ptl ht ui
lroc , nograph

display in smcl as text "Optimism-adjusted AUC = " as result %04.3f r(area) - `optimism'
display `optimism'

結構随所にテクいコマンドを仕込んでおります．

① frame create: データフレームを設定しています．中身はまだ入っていなくてもOKで、箱だけでもよいです．ここではAUCというデータフレームを作り、bsa（bootstrap resampling時の値）とorg（オリジナルデータへの当てはめ時の値）、それとモデルが走らなかったときにエラーとなるようにerrという変数を設定しました．frame postとすれば中に値を入れていくことを意味します．

②restoreコマンドのあとにpredict double xb, xbと配置することで、オリジナルデータでリサンプリング時に作ったモデル式を適用します．このときにxbオプションを使って線形予測子を返すのがポイントで、その次の工程のroctabに説明変数として投入可能です．この作業によってbootstrapで作ったモデルに基づいて線形予測子をオリジナルデータで作成し、AUCの計算をすることができるわけです．

③if !_rc {：エラーコードが返ってきてないとき、すなわちきちんとモデル式が回ったときを意味します．その前にcapture logitとしてプログラムエラーでも実行が止まらないように配慮しています．（コマンドの先頭にcaptureをつけることで万が一エラーになってもそのまま何事もなかったかのようにスルーしてくれます．generateなどを途中でいれてしまったときなどに便利です．最後に一気に走らせるときに、別の行ですでにそのコマンド作ってた！みたいなことが起こるので…）

④cwf AUCs：データフレーム（中にデータが入っていればそれも含めて）を表示することができます．cwf defaultとすれば元のデータセットが再表示されます．

こうして以下のような結果が導き出されます．

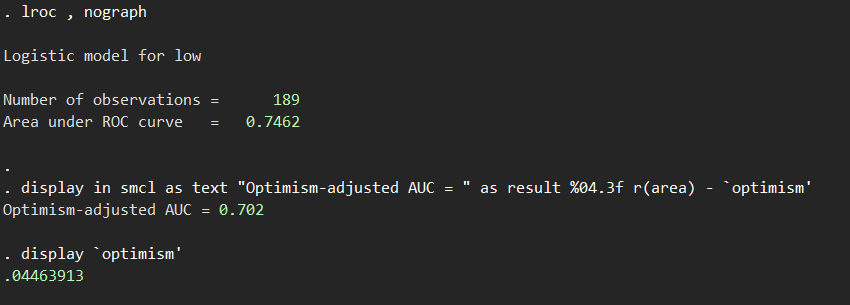
オリジナルデータではAUCが0.7462だったのですが、0.0446…のオプティミズムを引き算することで0.702というoptimism-corrected AUCが算出されました.

まとめ

今後はさらに多重補完後にどうするか、という問題に取り組みますが、ざっくりと言えば、このフレームワークをMI bootで実施する、ということになると思います．

先日の記事で紹介したBMJの論文では、

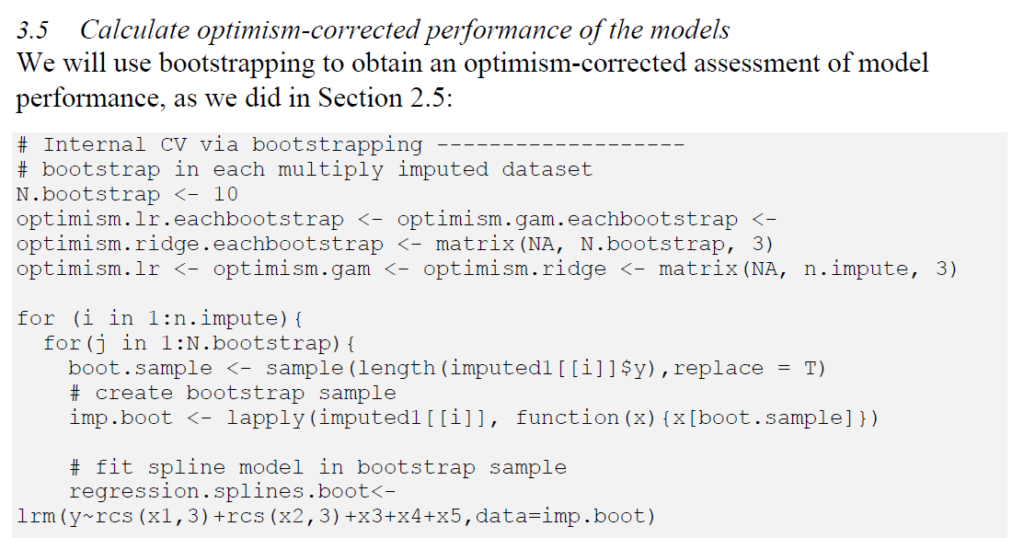
このように表示されていましたので、MIのコマンドが一番外のループになっており、それでよさそうです．mi extractでループを設定してひたすら回していき、最後にRubinで結果を統合することになると思います．（時間があれば作ってみます）

ちなみに今回の記事のアイキャッチ画像ですが、AIに生成してもらいました．optimismという言葉から想起されるようなイラストにしてくれ～と頼んだらこんなにかわいらしい絵が出てきました．