Bootstrapをプログラムで書いてみる

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています． ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて、今回は、Bootstrap resamplingをプログラムベースで実行することをやってみたいと思います．

この方法が使えれば色々と応用が利くと思いますので、マスターしておく価値はあるのではないかと思います．

元ネタはYoutubeのあるチャンネルからです．早口な英語でしたけど、かなりわかりやすく、プログラミングをくみ上げていくプロセスもわかりやすく説明してくれていたのでよかったです．

その内容を引用してまずはベーシックなコマンドを通じて実行してみることと、回帰分析において実装できるかを検証してみましたので、その結果をお示しします．（2021.7.17、元ネタ提供者に質問して正しいかどうかを聞いてみています．）

1．Bootstrap resamplingとは？

統計を使う目的の1つとして、「標本データを用いて母集団の性質を推測する」ことが挙げられます．

これは、母集団という理想的な条件をすべて兼ね備えた集団のことを指しますが、現実には母集団をすべて集めることはほぼ不可能です．

プラトンがいうところの「イデア」みたいなものです.

現実には理想的な集団を代表する「標本集団」をとってきてそれを分析することで大元の母集団で生じることを「推定」します．

しかしながら、標本集団というのは、同じ母集団から抽出したとしても現実問題としては毎回異なってきますよね．したがってその標本集団における統計量(比率、平均、分散など)は毎回異なるはずです．

ゆえに、標本データを用いて母集団の性質を推測する際には常に誤差が伴うという現実があります．

そこで、1970年代にエフロン (Efron) はブートストラップ (bootstrap) という方法を提唱しました.これは母集団の確率分布とかを考慮する必要がなく、ただ単純に1回だけとってきた標本集団を、もう一度くじ引きのような形で再度抽出することを繰り返します．これによって「不確実性」の要素を入れてとってきた標本にある種ゆさぶりをかけます．

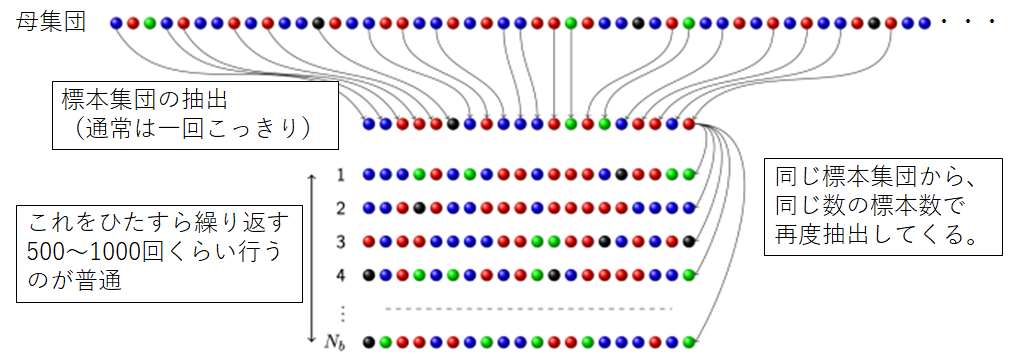
同じ数の標本を採ってくるのなら標本集団と何もかわらないのでは？と思ったりするかもしれませんが、同じ人が何度も抽出されたりするので、その心配はありません．

ただし、もうお分かりの方も大勢いらっしゃるとは思いますが、元のサンプルの選び方に偏りがあった場合にはいかにたくさん再抽出をしてもそのバイアスを消し去ることはできません．

どちらかと言えば標本データに依存した結果がでることを防ぐように、わざとボカシをいれているというか、ゆさぶりをかけるというか、そんなイメージなのだろうと思います．

なので、偶然の影響を減らしたいということ一点にのみメリットがある、ということかなと思います．

2．Bootstrap resamplingを実際にプログラムで書いてみる

今回は紹介した動画の中で解説されていた通りのことを再現してみたいと思います．

まずは仕込みで、適当にデータセットを作ってみます．10000レコードのランダム変数を以下のように設定してみます．再現性がとれるようにseedの設定もしておきましょう．

	clear
	set obs 10000
	set seed 210717
	generate X = rnormal()*2 + 4
	save originaldata.dta, replace

標準正規分布である数値を用いてXという変数を作ってみました．これの平均値と標準誤差を求めてみます．

ここでブートストラップの回数をまずは決めることにして、1000回としてみましょう．

そうすると、同じ標本から1000回の再抽出をでたらめに行うことになりますので、1000個の平均値を計算します．そしてその平均値が母集団の平均となります．（中心極限定理ですね）

それからこの1000個の標準偏差が求めるべき標準誤差となります．

	local boots = 1000
	clear
	set obs `boots'
	gen store_means = .

このようにすることで、求めるべき平均の平均（母集団の平均）が入る”箱”ができます．

	use originaldata.dta, clear
	bsample
	sum X
	local mean_got = r(mean)

これが1回の再抽出後のデータから得られた平均値です．これを再抽出するたびに結果を入れていくようにします．

• 1回目の結果を1行目に
• 2回目の結果を2行目に
• 3回目の結果を3行目に
• …
• n回目の結果をn行目に

といった具合にするのでループを使います．1000回行こなうのでlocal boots = 1000 とやった`boots’をそのままローカル変数として引っ張ってきましょう．

	local boots = 1000
	clear
	set obs `boots'
	gen store_means = .

forvalues i = 1(1)`boots' {
	preserve
		use originaldata.dta, clear
		bsample
		sum X
		local mean_got = r(mean)
	restore
		replace store_means = `mean_got' in `i'
	}

	sum store_means

このようにすることで、i = 1から始まって1000までやりますよ、となります．

毎回もとのデータセットを開いてbsampleというコマンドで再抽出を行います．

このbsampleというコマンドは、特に指定しなければデータセットと同じ数だけ再抽出します．

前述した通りまるきり同じデータにならないのは同じ人が選ばれうるからです．つまりは復元抽出を行っている、と考えてもよいでしょう．

store_meansという変数は冒頭で作った”箱”なので、そこに次々にその標本ごとの平均値が書き込まれていきます．それが1000回まで終わったところで、結果だけが入ったデータセットが出来上がります．

この結果だけの変数で平均と標準偏差を求めると、ほしかった母集団の平均と標準誤差が手に入ります．

if以下はどちらでもいいのですが、かっこいいので入れてみました．100サンプル計算する間にどのくらい時間が経過しているのかを日付時間のスタンプを表示することによって見える化してくれます．

	local boots = 1000
	clear
	set obs `boots'
	gen store_means = .

quietly {
	forvalues i = 1(1)`boots' {
		if floor((`i' -1)/100) == (`i' - 1 )/100 {
			noi dis "Working on `i' out of `boots' at $S_TIME"
		}
		preserve
			use originaldata.dta, clear
			bsample
			sum X
			local mean_got = r(mean)
		restore
			replace store_means = `mean_got' in `i'
	}
}
	sum store_means
	save boot_results.dta, replace
	use originaldata.dta, clear
	mean X

すると以下のような結果が得られました．

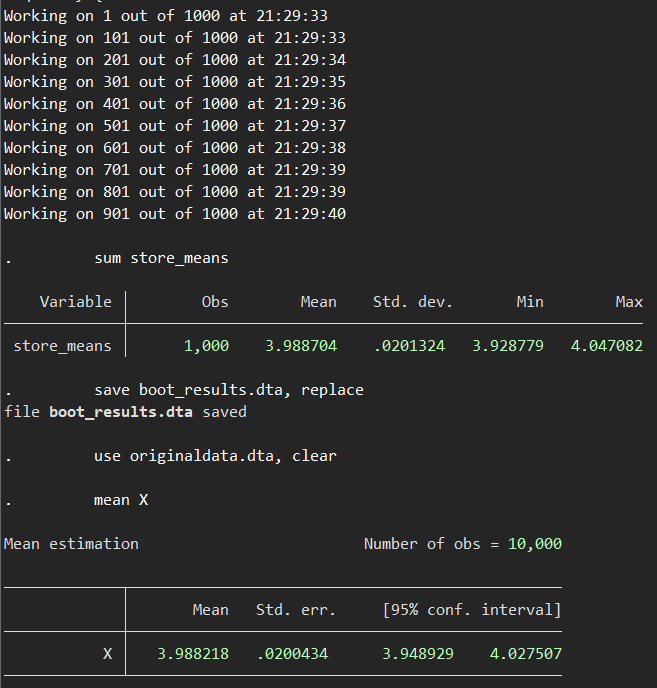
上がBootstrap resamplingで得られた結果を統合したもので、Meanはそのまま、Standard deviationはStandard errorと解釈されます．

そして下がもともとの標本データから得られた平均と標準誤差です．

かなり近い値になったのではないでしょうか．

3．回帰分析で実装してみる

これを回帰分析でもやってみたくなりますね．

というのも、予測モデルを作成するときにinternal validationをみるときにbootstrap法が紹介されていますね．そういったモチベーションからこのプログラムを使うことを想定しています．

ところで、回帰分析の場合には、prefix commandでbootstrap: regress … と実施することもできます．

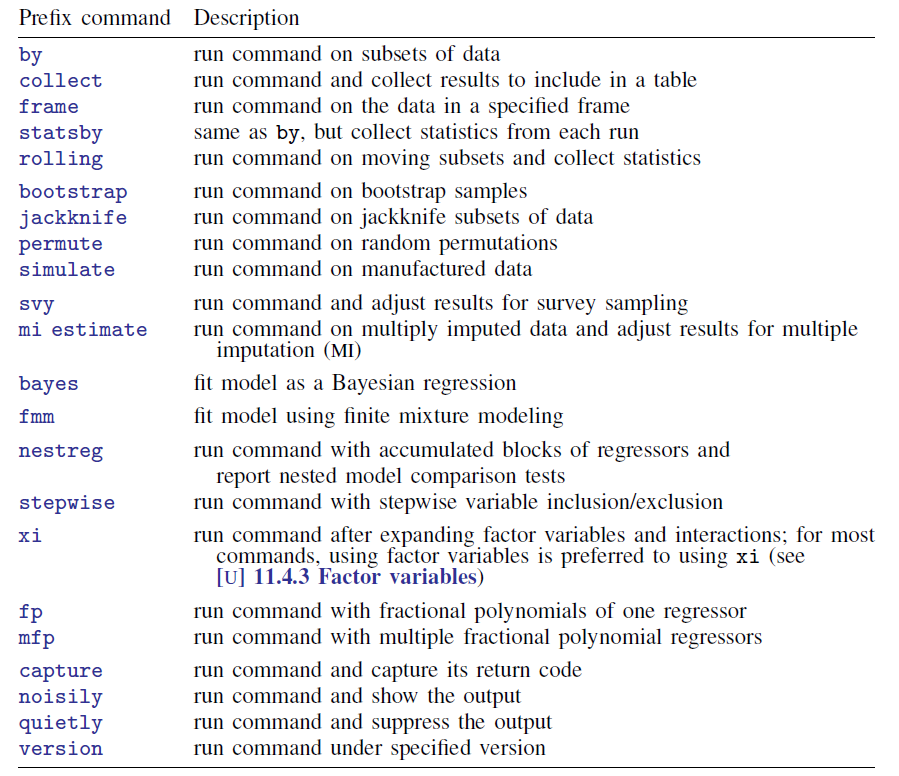
この中にあるbootstrapについて、どのようにworkするのでしょうか．

bootstrap performs nonparametric bootstrap estimation of specified statistics (or expressions) for a Stata command or a user-written program. Statistics are bootstrapped by resampling the data in memory with replacement. bootstrap is designed for use with non-estimation commands, functions of coefficients, or user-written programs. To bootstrap coefficients, we recommend using the vce(bootstrap) option when allowed by the estimation command.

ノンパラメトリックなbootstrap estimationを実施するコマンド。メモリ上のデータを再抽出することでbootstrapが行われる。このコマンドはnon-estimationコマンドであり、推定値をbootstrapするときにはvce(bootstrap)というオプションをつけることでestimation コマンドで使うことを推奨する。

とのこと。ということで、まずはサンプルデータを使って

1. Bootstrap resamplingしない普通の重回帰
2. おススメどおり、vce(bootstrap)のオプションをつけてみる
3. prefixでbootstrapをつける
4. 手作りのbootstrapをやってみる
5. SEのみbootstrapしてみる

という流れで実施してみましょう．

sysuse auto, clear
regress mpg weight gear foreign
regress mpg weight gear foreign, vce(bootstrap, rep(1000))
bootstrap, reps(1000): regress mpg weight gear foreign

まずは通常の重回帰ですが、

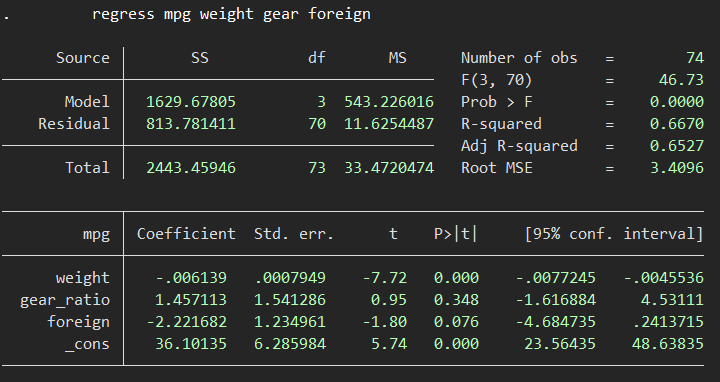
続いてvce(bootstrap)

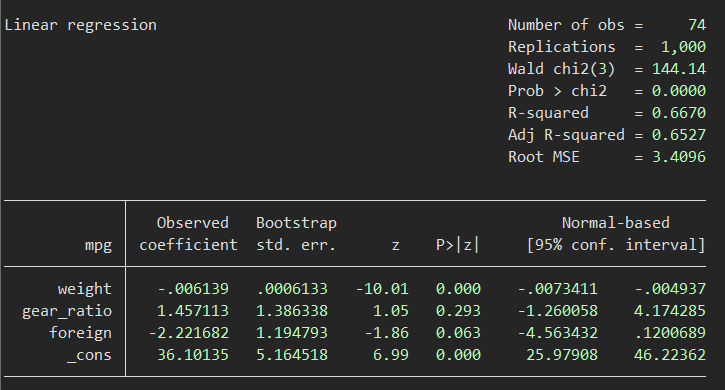
点推定値は変わっていませんが、標準誤差が変わりました。結果としてP値と信頼区間に違いがみられます.

続いてprefix

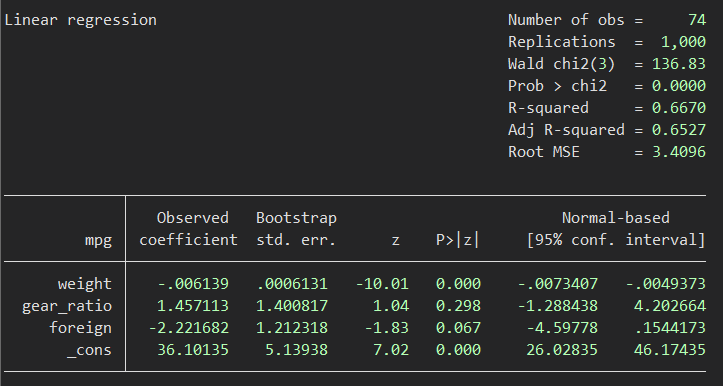
やはり点推定値は寸分の違いもありません．そして標準誤差ですが、こちらはそれほど大きくは違わないものの、微妙に違っています．推奨通り前者を採用したほうがよいのでしょうか．

(2021/7/18追記)Stataが提供するプログラムは点推定値はそのままで、SEのみBootstrapしているようです．

そして、動画の主に問い合わせてみたところ、次のようなやり取りと回答を得ました．

In Stata, the bootstrap command can also work but the coefficients do not change and only standard errors change.

sysuse auto, clear

regress mpg weight gear foreign

regress mpg weight gear foreign, vce(bootstrap, rep(1000))

In the second command, you can get the coefficient and SE. But the coef is actually the same as the original model. What is the difference?

Stataだとブートストラップのコマンドでは点推定値は変わっていなくてSEだけ変わってるんさねー。試しにやってみたんだけど、二つ目のプログラムだと点推定値はブートストラップしなかった場合とかわらなかったんさね。どういうことなん？

彼からの返答です．

The second command is estimating the coefficient by regular OLS and only the standard errors by bootstrap. This is actually a good idea if you plan to use them for hypothesis tests, as it helps any hypothesis tests done after the fact be sure they’re comparing the right things.

あー、点推定値はそのままOLSでやったんとかわらんがね。SEだけブートストラップしたんだがね。仮説検定のときにゃあいいアイディアだと思うよ。正しいものを比べっこしたっつー事実のあとに仮説検定できるでねー。

ということでした．UCLAのサイトを見るとそのあたり詳しく理解できると思います．これについては改めて解説させていただきます．

さて、プログラムベースです．

	local boots = 1000
	clear
	set obs `boots'
	gen beta_weight =.
	gen beta_gear =.
	gen beta_foreign =.
	
quietly {
	forvalues i = 1(1)`boots' {
		if floor((`i' -1)/100) == (`i' - 1 )/100 {
			noi dis "Working on `i' out of `boots' at $S_TIME"
		}
		preserve
			sysuse auto, clear
			bsample
			regress mpg weight gear foreign
			local weight = _b[weight]
			local gear = _b[gear]
			local foreign = _b[foreign]
		restore
			replace beta_weight = `weight' in `i'
			replace beta_gear = `gear' in `i'
			replace beta_foreign = `foreign' in `i'
	}
}
	sum beta_weight beta_gear beta_foreign

こちらは点推定値も異なっています．

4．生存時間分析に実装してみる

さて、次は生存時間分析でも同様にやってみました．

bootstrapなしとありでやってみます．

webuse hypoxia, clear
stset dftime, failure(dfcens==1)
stcox age hgb ifp tumsize, nohr
stcox age hgb ifp tumsize, nohr vce(bootstrap, rep(1000))

なしでは

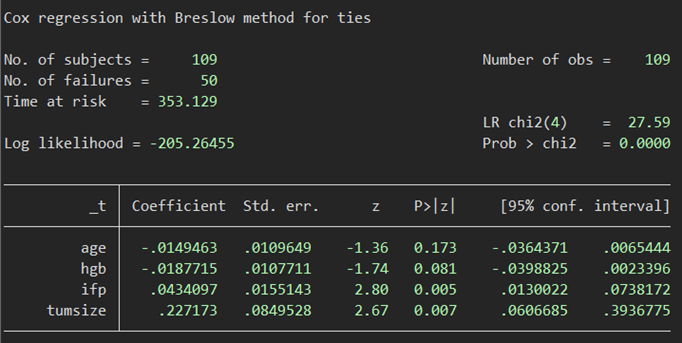
ありでは

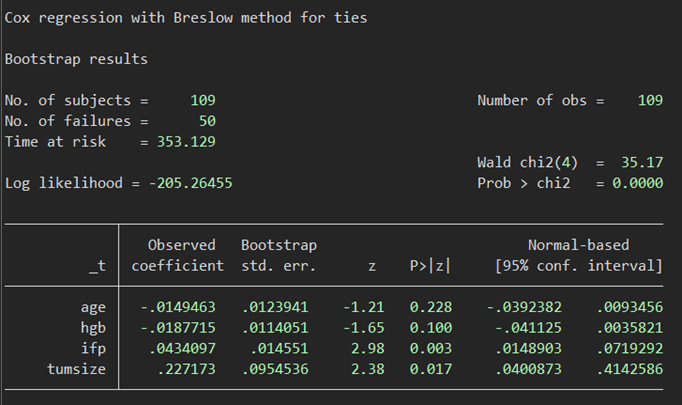
やはりこの場合にも点推定値は寸分の狂いもありません．

プログラムを作って実行してみたところ、以下のようになりました．

	local boots = 1000
	clear
	set obs `boots'
	gen beta_weight =.
	gen beta_gear =.
	gen beta_foreign =.
	
quietly {
	forvalues i = 1(1)`boots' {
		if floor((`i' -1)/100) == (`i' - 1 )/100 {
			noi dis "Working on `i' out of `boots' at $S_TIME"
		}
		preserve
			sysuse auto, clear
			bsample
			regress mpg weight gear foreign
			local weight = _b[weight]
			local gear = _b[gear]
			local foreign = _b[foreign]
		restore
			replace beta_weight = `weight' in `i'
			replace beta_gear = `gear' in `i'
			replace beta_foreign = `foreign' in `i'
	}
}
	sum beta_weight beta_gear beta_foreign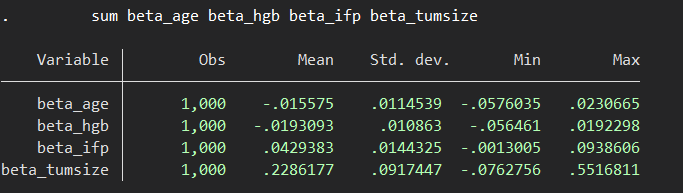

こちらはやはり点推定値も異なりますね．

まとめ

ここまでの解説を見る限り方法としては次の5つのやり方があり、それぞれ違う結果がでてきました．

1. Bootstrap resamplingしないオリジナルデータを使った解析
2. vce(bootstrap)のオプションをつけて解析
3. prefixでbootstrapをつけて解析
4. 手作りのbootstrapで点推定値とSEをそれぞれ求める
5. SEのみbootstrap

次の記事では最後のバージョンについて解説するのと、様々な場面でどのようにBootstrapを行うのか、考えてみたいと思います．