前回の記事では競合リスク解析の理論について説明しました.いよいよ今回は実践編です.
残念ながらStataでは競合リスクを考慮したCumulative incidence法でのグラフを描いて必要な統計的な検討を行うためのコマンドが存在しないため、Straightforwardにいかない、という事実があります.
さらに、カプランマイヤー法におけるLog-rank testに相当する、Cumulative incidence法におけるGray’s testは残念ながら、別のソフトを使うしかなさそうです.(どなたかご存知だったら教えてください)
もっとも、Stataとしても全く方法がないわけではありません。Gray検定に準じた方法として”Pepe and Mori test”が使えます.
PepeとMori…『森の中のPepe』みたいな物語のタイトルがありそうですね.実際にこの検定法を使っている論文に出合ったことがないので、やはり不十分と言わざるを得ないでしょう.
そこで現状では他のソフトを使う、という屈辱的な(?)選択をせざるを得ません.しかし、Cumulative incidence法のグラフまで違うソフトで描いてしまうと、グラフがStataで統一できず、はっきり言って気持ち悪いです.
せめてグラフまではStataで描いて、検定結果だけ他のソフトから輸入してしまいましょう、というのが今回の記事の趣旨になります.
1.必要なコマンドのインストール
使うコマンドは”stcompet”ですが、PePe and Moriを使いたければ”stpepemori”もインストールする必要があります.
*** 必要なコマンドをインストール
ssc install stcompet
ssc install stpepemori
*** データセットを展開
use dataset, clear /// 何らかのデータセット2.グラフの作成
生存時間分析をするという宣言をするところまでは一緒ですが、ここであらたに”stcompet”でcumulative incidence functionを定義します.
### Syntax ###
.stcompet newvarname = { ci | se | hi | lo } [[newvarname = ...] [...] ] ///
[if exp] [in range] , compet1(numlist) [compet2(numlist) compet3(numlist) ///
compet4(numlist) compet5(numlist) compet6(numlist) by(varname) allignol level(#) ]
/// 競合イベントを6つまで定義可能, byの中に曝露因子/介入因子を入れる
/// ci: cumulative incidence function
/// se: standard error of the CI
/// hi: 信頼区間上限 <- ln[-ln(Cumulative Incidence)]
/// lo: 信頼区間下限 <- ln[-ln(Cumulative Incidence)]
/// level: 信頼区間のレベルを規定.Defaultでは95%興味のあるイベントが「status = 1」、競合イベントが「status = 2」として、薬剤投与の有無(drug)の影響をみるには以下のように書きます.
stset time, failure(status = 1)
stcompet cif = ci, compet1(2) by(drug)
/// 新たに"cif"という変数を作成してcumulative incidence functionを設定
*** ここでcifを興味のあるイベント、曝露または介入因子によって分ける
gen cif_local_control = cif if status == 1 & drug == 0
gen cif_local_treatment = cif if status == 1 & drug == 1これを元にしてグラフを作成します.
twoway line cif_local_* _t , connect(J J) sort ytitle(Cumulative Incidence)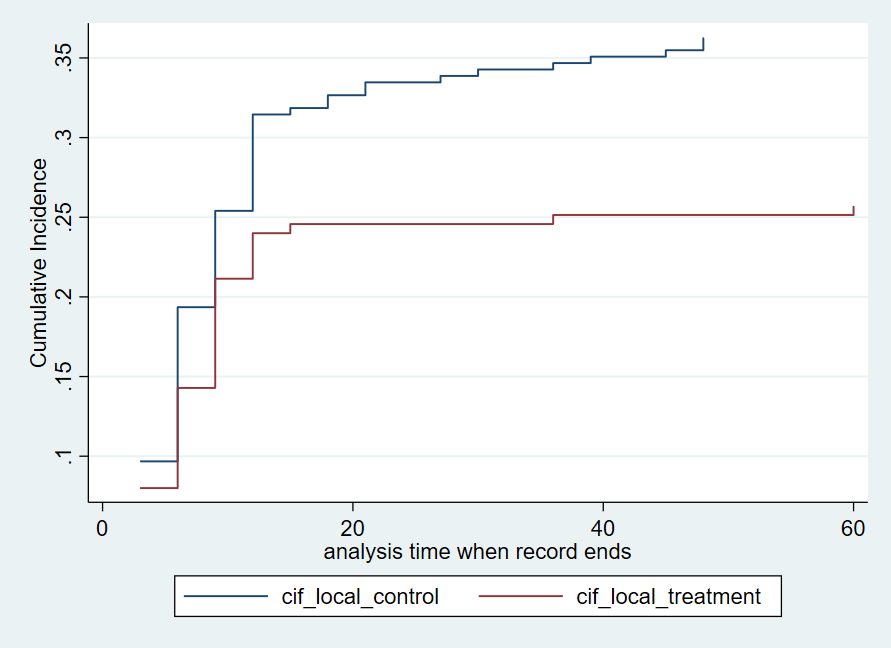
ちなみに通常のカプランマイヤー法で描くのは超簡単で、コマンドで一発でできます.適度に軸のスケールを合わせると次のような感じになります.
sts graph, by(drug) failure yscale(range(0 0.4)) ylabel(0(0.05)0.35)
上記2つを比べると、カプランマイヤー法よりもCumulative incidence法の方が全体的に発生率が低く出ることがわかります.問題はCumulative incidence法でグラフを描こうとすると、ゼロ付近がないので、少し細工が必要になります.
3.グラフの微調整
- イベント未発生、観察期間ゼロの人を各群に1人ずつダミーで作成
- 生存時間分析で宣言したときに作成された変数も細工が必要
use dataset, clear
*** ダミー用に2行追加
set obs `=_N+1'
set obs `=_N+1'
*** 各群に設定
replace drug = 1 in 424
replace drug = 0 in 425
*** アウトカムは発症しない
replace status = 0 in 424/425
*** 生存時間分析宣言~CIFの設定
stset time, failure(status = 1)
stcompet cif = ci, compet1(2) by(drug)
gen cif_local_control = cif if status == 1 & drug == 0
gen cif_local_treatment = cif if status == 1 & drug == 1
*** 最後の調整として、生存時間分析宣言でできた変数も少し細工する
replace cif_local_control = 0 in 424/425
replace cif_local_treatment = 0 in 424/425
replace _t0 = 0 in 424/425
replace _t = 0 in 424/425
*** グラフ作成
twoway line cif_local_* _t , connect(J J) sort ytitle(Cumulative Incidence) 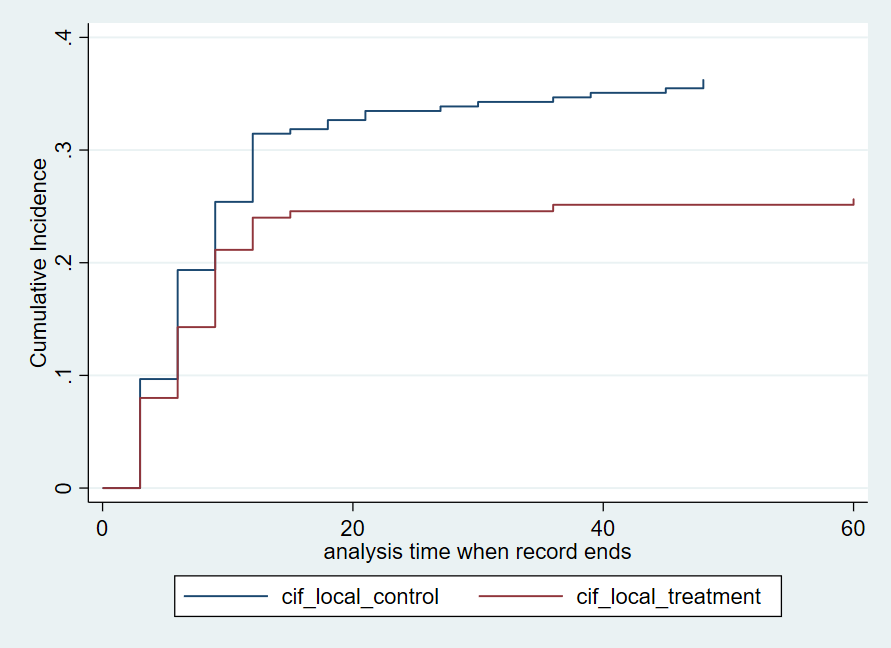
Gray’s testの代わりにPepe and Mori testを行うことにして、
stpepemori drug, compet(2)これででた答えがP = 0.030であった.
ちなみにEZRでだすと一瞬で出てくるため、いままのでの苦労は何だったのか?という気持ちになってしまう.(P = 0.027)
しかしグラフの見た目に統一感がなくなってしまうので、ここはやはり頑張ってStataで描きたいところです.twowayで描けるので自分でカスタマイズできるのがいいですよね.
ちなみに多変量解析であるFine & Gray モデルはさすがに実装されておりますので実施可能です.
stset time, failure(status = 1)
/// 生存時間分析を宣言
stcrreg drug, compete(status = 2)
/// Fine & Gray モデルを実行(drugのあとに変数リストを追加すれば多変量解析可)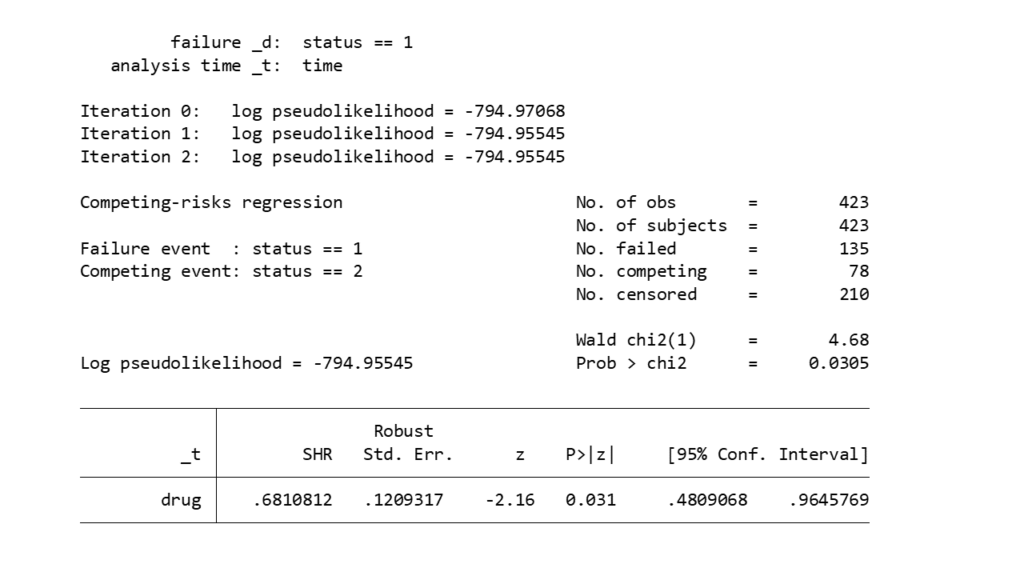
結果はSHR (sub hazard ratio)で返ってきます.
ちなみに、Cox PH modelsではstrataオプションで層化Coxモデルが行えたのですが、Fine & Gray モデルではstrataオプションは使えません.多施設共同研究で施設ごとにベースラインリスクが異なることを考慮した解析はコマンドベースでは実施できないことになります.Rにはコマンドがあるようですが、詳細はこちらに譲ります.
4.まとめ
Stataで競合リスクを考慮したCumulative incidence法によるグラフ作成、および検定まで行ってきました.Straightforwardに行かない部分は他のソフトの力を借りましょう.StataでもGray検定を実装してくれる日を切に願います……


コメント
[…] 前回、前々回の記事では競合リスク解析の理論と実践の初歩について説明しました.今回はちょっとした応用編です. […]
失礼いたします。質問です。
「Stataでは競合リスクを考慮したCumulative incidence法でのグラフを描いて必要な統計的な検討を行うためのコマンドが存在しない」とのことですが、以下のURLにあるstcrregとstcurveを組み合わせて用いるグラフの描き方では不具合があるのでしょうか。
https://www.lightstone.co.jp/stata/stata11_competing_risks_regression.html
ご質問ありがとうございます。これは実は自分も最初そうだと思っていたのですが、どうやら違いそうということがわかってきました。
stcurveですと、セミパラメトリックなので一見するとCIFっぽく見えるのですが、SHRに従ってもとのCIFを分割することになるので、実際の事象で描いたものと違ってしまうんですね。
ライトストーンのHPにあるグラフもよくみるときれいに平行になっていますよね。
(群分けをしなければいいのかもしれませんが、そんなグラフを描くことはありませんよね。)
なるほど。わかりやすく教えていただき、ありがとうございました。