順序ロジスティック回帰について | 医療統計とStataプログラミングの部屋

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています．ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて、今回は順序ロジスティック回帰をStataで実行するための方法と、前提の確認、Goodness-of-fit test的な検定についてまとめてみます．

（なお、今回の記事の元ネタはPennsylvania大学の疫学・生物統計学の授業からです．）

1．どんな場面で使うか？
2．前提確認に必要なコマンドを入手する
3．順序ロジスティック回帰を実行する
4．順序ロジスティックの前提条件（Proportional odds assumption）
5．まとめ

1．どんな場面で使うか？

疾患の重症度、Stage、連続変数を特定のカットオフ値で区切ったカテゴリー変数など、順番に次のステージに上がっていくような状況が考えられるときに適用することを検討します．

no disease, mild, moderate, severe
Stage A, B, C, D
healthy weight, overweight, obese (BMIに基づくカテゴリー)

Proportional odds modelで1つ手前のカテゴリーと比較してどのくらい確率が変化したかを表します．

この前提をきっちり確認する作業が必要になる点が通常のロジスティック回帰との違いです．

2．前提確認に必要なコマンドを入手する

ここでは”brant”と”listcoef”を入手するために、

.findit spost13

としてみてください．

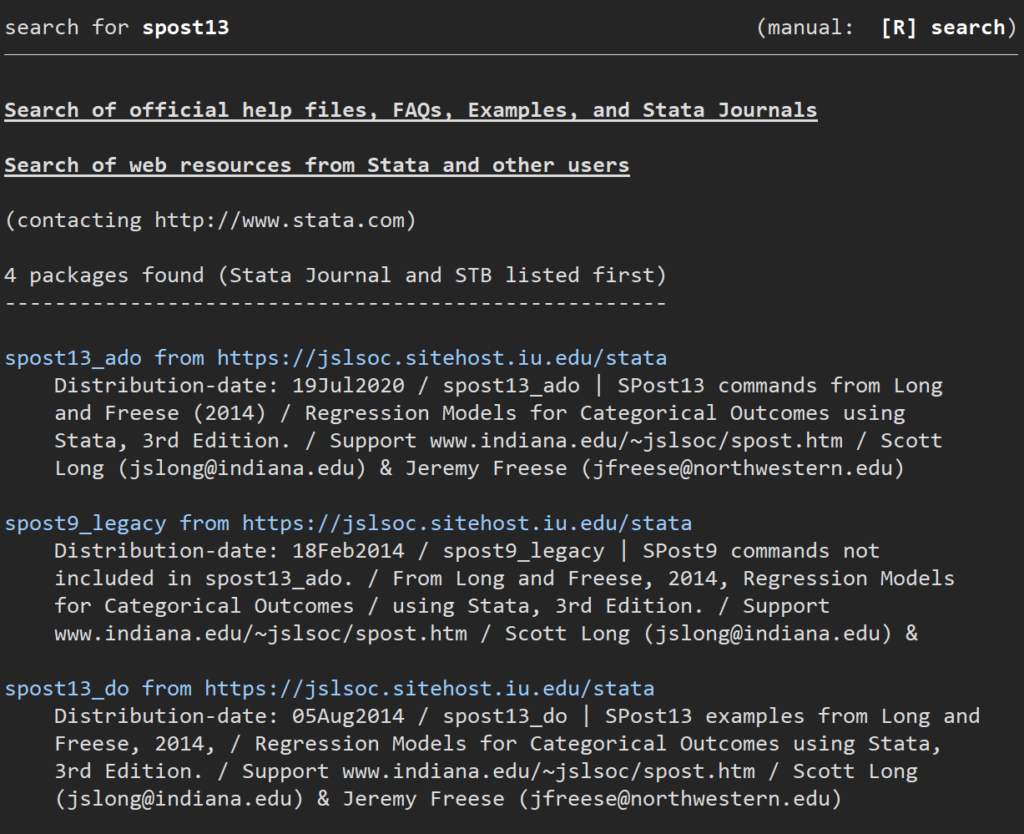
このado fileを入手するとあとの前提確認で役に立ちます．

ちなみにspost9を入れるように授業で言われたのですが、Stataのバージョンが上がってからはこちらのプログラムではうまくいかなくなりました．

“variable cut1 not found”

“conformability error”

などの表示がでてきてうまく走りません．こういうのがでてきているときは、プログラム自体がうまく作動しないので根本的な解決が必要になります．そこで最新版（spost13_ado）を入れることになりますが、spost9_adoが先に入っていると、以下のコメントが出てきてしまいます．

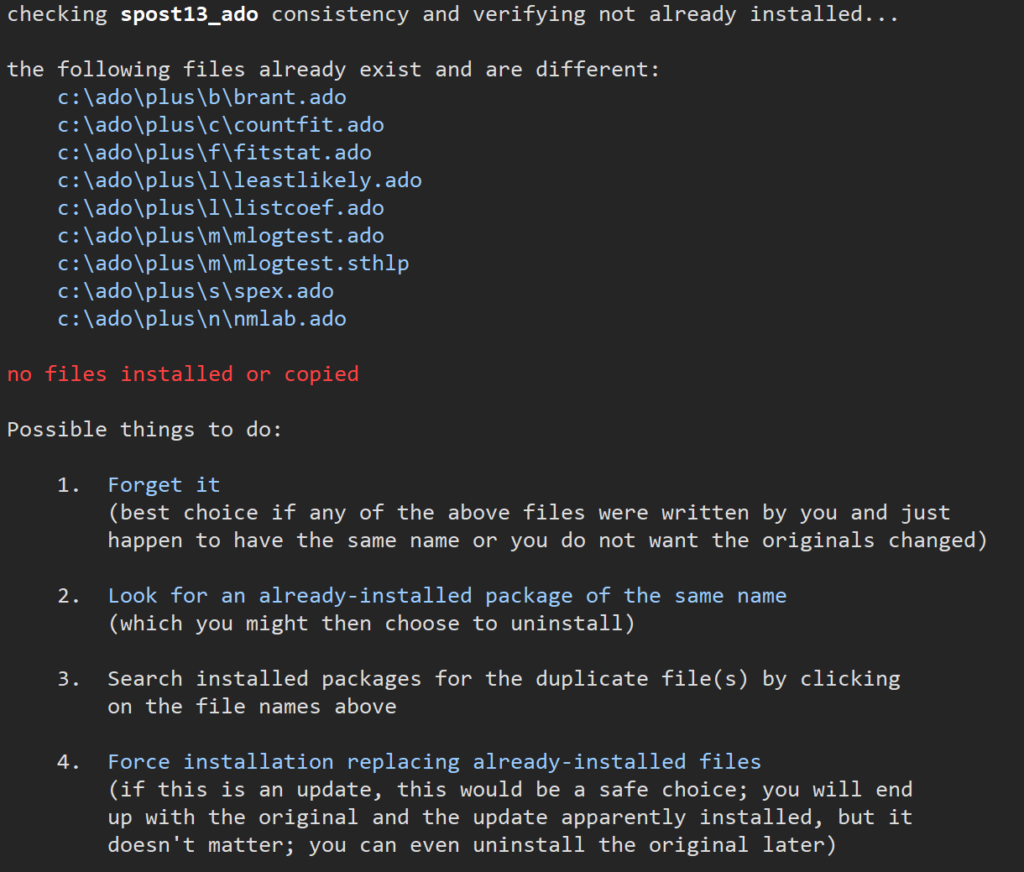
この、”4．Force installation replacing already-installed files”を選択してクリックします．すると、

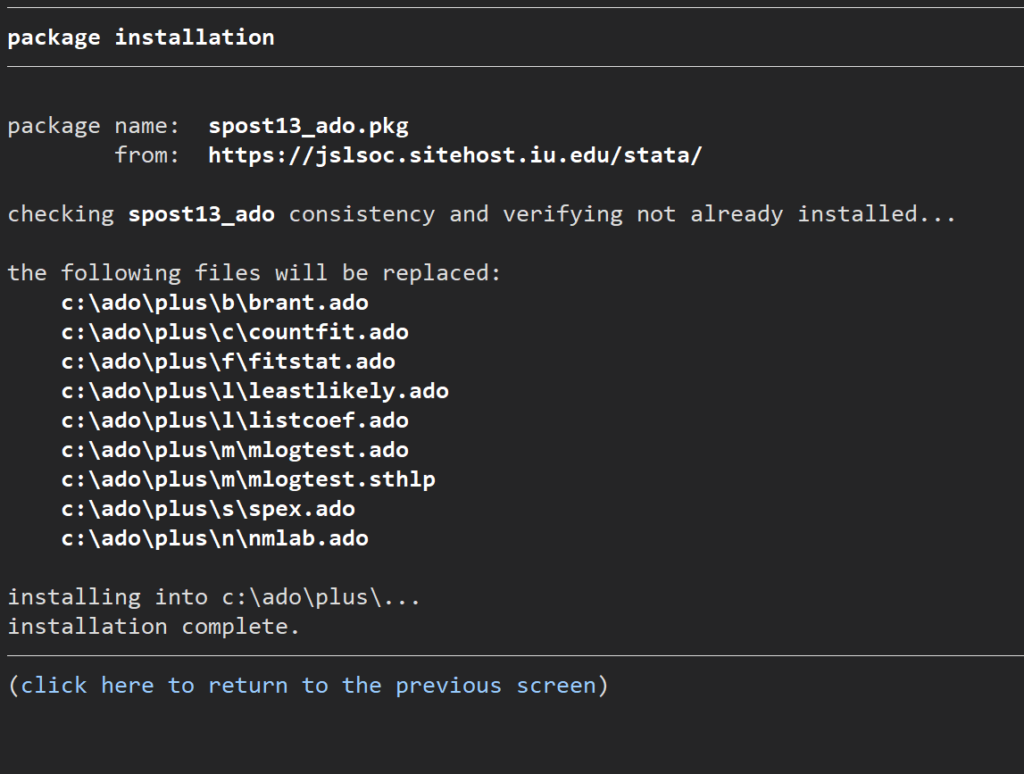
これで問題無くプログラムが動きます．

3．順序ロジスティック回帰を実行する

ここまでくると実際にやってみたくなりますので、ネット経由でlbwという名前のデータセットをとってくるとしましょう．

webuse lbw, clear
generate bwt4n=0*(bwt<=2500) + 1*(bwt>2500 & bwt<=3000) + 2*(bwt>3000 & bwt<=3500) + 3*(bwt>3500 & bwt~=.)  /* カテゴリー化する */
tabstat bwt, by(bwt4n) s(n min max)　/* 値の範囲を確認 */
ologit bwt4n lwt　　/* 順序ロジスティックのコマンドを走らせる */
ologit bwt4n lwt, or　/* オッズ比で表示させる */
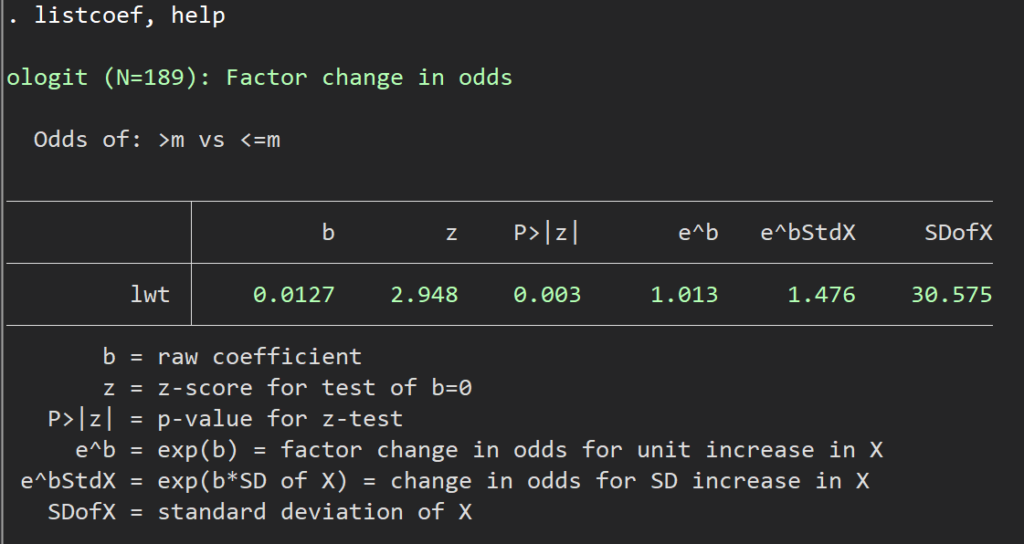
listcoef, help

順序ロジスティックの結果はこのように表示されます．

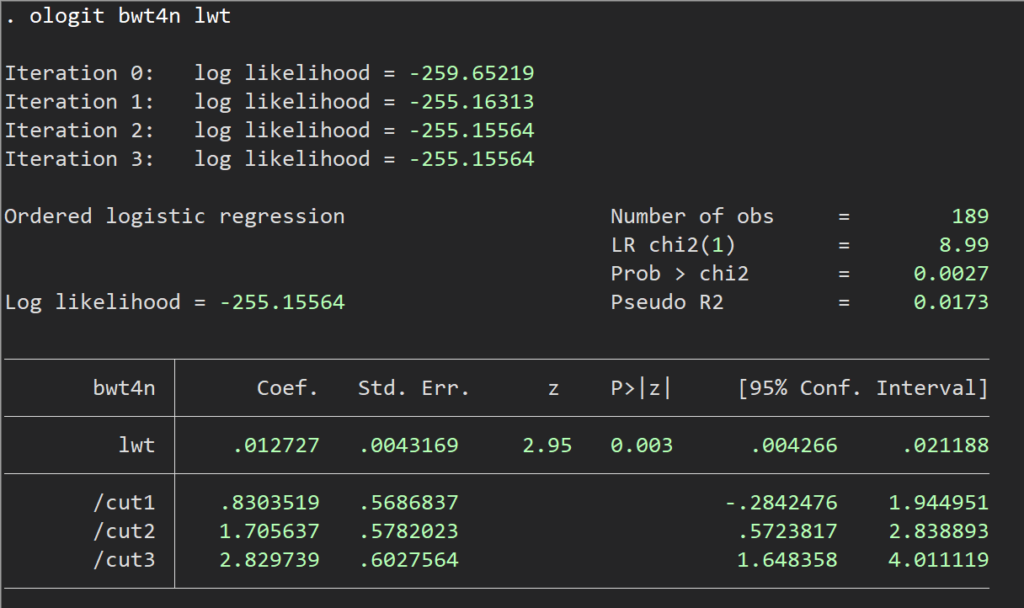
ちなみにこのlistcoefというコマンドは、ロジット、Z値、P値、オッズ比（指数変換後）などの値が並びます．

4．順序ロジスティックの前提条件（Proportional odds assumption）

比例ハザード性の確認みたいな趣もありますが、これは要するにno disease からmildにあがるときと、mildからmoderate、moderateからsevereに上がるときが一様なオッズ比になっているかどうかという意味になります．ここで使えるのは“brant”というコマンドです．

ologit bwt4n lwt　　/* 順序ロジスティックのコマンドを走らせる */
brant, detail

すごく乱暴な言い方をさせて貰えば、最後のP値が0.05より大きければparallel regression assumption, proportional oddsの前提は最低限よいことを意味します.

これだけでも文句は言われないと思うのですが、ざっくりとしたgoodness-of-fit testについても授業で学びましたのでご紹介します.

多項ロジスティックモデルを同時に実行して、尤度をそれぞれのモデルで得ておき(L0を順序ロジスティック、L1を多項ロジスティックで得たとして)、-2(logL0 – logL1)をχ2(p(k -2))分布で比較、P>0.05など十分大きいことを示すことで適合度を検定する、というモノです.

理屈は抜きにして方法だけ掲載しておきます.

qui mlogit bwt4n smoke lwt
scalar logL1 = e(ll)
** Log-likelihood from multinomial model
scalar list logL1     /* logL1 = -250.45429 */
**Fit the ordinal model
qui ologit bwt4n smoke lwt
scalar logL0 = e(ll)
** Log-likelihood from ordinal model
scalar list logL0     /* logL0 = -251.63498 */
scalar neg2diff = -2*(scalar(logL0)-scalar(logL1))
** -2*(log(L1) - log(L0))
scalar list neg2diff
  /* neg2diff = 2.3613915
 */
** compare with Chi-square(p*(k-2))
** Here p = 2 and k = 4 , so p*(k-2) = 2*2 = 4
scalar pvalue = chi2tail(4,neg2diff)
scalar list pvalue    /* pvalue =   .6696154 */