心血管病のリスク予測JASN2022

疫学

本カテゴリー「論文紹介」では管理者の独断と偏見と気まぐれで選んだ論文を解説します．

論文は図表の貼り付けや結果の細かな紹介はできませんが、最小限の結果（abstractで公開されている範囲）を引用する形で紹介していきます。また、図表もそのまま貼り付けることはせず、オリジナルのイメージ図に替えて掲載致します．

主旨としては管理者自らの疫学・統計学・臨床医学上の個人的解釈とし、Stataのコード紹介なども行っていきます．内容の詳細がご覧になりたい場合にはぜひ本文を正式に入手してください．

なお、内容の是非に踏み込んだコメントも致しますが、本ブログは情報提供だけを目的としたもので、医学的アドバイス（診断、治療、予防）の代わりになるものではありません．本ブログの内容はあくまで個人の見解に基づいたものであり、所属組織とは関係ありません．また診療目的でのアドバイスやご質問も受け付けておりませんので宜しくお願いいたします．

さて、今日ご紹介する論文は、CRIC研究のデータを使ったCVDリスク予測に関する研究で、以前ご紹介した、CKD patchの論文を発表したJohn Hopkinsのグループからの報告です．

今回紹介したかったのは、主に方法論です．結果のインパクトよりも、他にも応用が利きそうな方法論を紹介してくれた点で非常に価値のある論文だと思いました．タイトルは、

Joshua D. Bundy et al. Risk Prediction Models for Atherosclerotic Cardiovascular Disease in Patients with Chronic Kidney Disease: The CRIC Study. J Am Soc Nephrol 2022; 33: 601-611

1．要旨

ごく簡単にこの論文の要点をまとめておきます．

10年先の心血管病の発症予測には2013年に発表されたACC/AHAのガイドラインで紹介されているリスク予測ツールが用いられてきました（traditional ACC/AHA pooled cohort equation）．こちらに示すように、この予測ツールには、CKDに関する情報が含まれていませんでした．

  • age
  • sex
  • race/ethnicity
  • total cholesterol
  • high-density lipoprotein (HDL) cholesterol
  • systolic blood pressure (BP)
  • use of BP-lowering medications
  • history of diabetes
  • current smoking

そこにeGFRやUACRを入れると予測の精度が向上することを発表したのが前述の論文で、CKD patchです．

今回はさらにそこに新たに様々な要因を入れて新しいモデルを作ってみよう！ということで、米国を代表するCKDコホートである、CRIC研究のデータを使ってモデルを作成、比較することにしたわけです．

ここで、CVDは動脈硬化性CVDに限定して検討されています（Atherosclerotic cardiovascular disease, ASCVD）.

モデルの比較としては、

  1. traditional ACC/AHA pooled cohort equation: 係数を元のモデル通り
  2. Model 1: ACC/AHA PCE model の係数をCRICに最適化
  3. Model 2（CRIC clinical model）: 上記モデルの因子＋clinically readily availableなその他の要因を入れてCRICに最適化したモデル
  4. Model 3 (CRIC enriched model) : 上記の因子に加えてその他さまざまなバイオマーカーも入れてCRICに最適化したモデル

で比較しています．

2．モデルの生成に用いられた方法

新たなモデルに組み込まれた候補因子は、

  • metabolic factors: BMI, HbA1c, 血糖降下薬, insulin, 尿酸, ホモシスチン
  • kidney disease: eGFR (cystatin C入り), UACR, Hb, UN, albumin, 重炭酸, NGAL
  • lipid metabolism: LDL, VLDL, TG, スタチン, Apolipoprotein A1, Apolipoprotein B
  • mineral metabolism: Ca, P, FGF23
  • inflammation factors: WBC, hsCRP, Fibrinogen, TNF-α, IL-6, IL-1RA, IL-1β
  • vascular factors: 拡張期血圧、ABI
  • cardiac biomarkers: Troponin-I, Troponin-T, NT-ProBNP

黒字の要因から選択されたものがModel 2となり、すべて含めてModel 3となりました．

多変量モデルは、Cox比例ハザードモデルをprimaryとし、死亡を競合イベントとしたFine＆Gray modelを第2アプローチとして実施しています．

変数選択の方法としては、Backward eliminationをP値（＜0.05）に基づくパターンとAICに基づくパターンのいずれも採用し、LASSO, λ=1 SE　も比較されました．

LASSO、自分では経験がなかったのでよくわからなかったのですが、Supplementary methodsに詳細な記載がありました．

We tuned the LASSO model using cross-validation, and identified the regularization penalty that minimized cross-validated error (i.e., λ=minimum). To select parsimonious models with similar predictive performance to models utilizing λ=minimum, we used a regularization penalty one standard error higher than that which minimized cross-validated error, as recommended

JASN 33: 601–611, 2022

モデルを作成したデータセット内でクロスバリデーションを行って最適な変数選択、係数の算出を行ったようです．知らんけど．

3．モデルの比較に用いられた方法

モデルの比較にはdiscrimination, calibration, and overall goodness of fitの3つの軸で検討します．

Discriminationは、将来イベントを起こす人と起こさない人を正しく判別するためのモデルの性能のことを指します．10年後までのイベント発現に関して、area under the receiver operating characteristic curve (AUC)　を求めます．

Calibrationは、観察されたアウトカムと予測モデルによる予測確率の一致をプロットして確認することを言います．

観察されたリスクは、死亡を競合リスクとして考慮した、Cumulative incidence functionを用いて推定します．(stcompetを用いて求める、Aalen-Johansen estimates)

The scaled Brier score, または、index of prediction accuracy (IPA) はdiscriminationとcalibrationの両方に関する情報を含みます．さらにoverall goodness of fitとしても使えるとのことです.

ここで初耳のIPAについてですが、まずはBrier scoreというものが何なのかを先にご説明します．

結果xiから予測値qiを引いた値を二乗した平均値

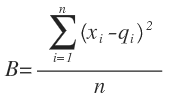
次の日の天気を3人で予想する状況を思い浮かべてみましょう．

太郎君は0.75の確率と雨と予想しました．

次郎君は0.5の確率と雨と予想しました．

三郎君は0の確率と雨と予想しました．

そして次の日は雨でした．このとき、

太郎君は(1-0.75)^2 = 0.0625, 次郎君は(1-0.5)^2 = 0.25, 三郎君は(1-0)^2 = 1

これを何度も繰り返してその都度出てきた値を平均すると得られます．

1に近いほど予測精度が悪い、0に近いほどよい、というものになります．

そして、index of prediction accuracyというのは

IPA=1 − BrierScore(Prediction model)／BrierScore(Null model)

で与えられます．

Prediction modelが太郎君、Null modelが三郎君だとすると、分数のパートは0に近づきます．なので1が最大値となります．逆だと分数パートは1より大きくなり、マイナスの値をとるときはイケてないモデル、という解釈が成り立ちます．

また、このモデルの95%信頼区間は次のように与えられます．

A higher IPA indicates a better performing model, an IPA of 1.0 indicates a perfect model, and an IPA ≤0 indicates a useless model. Performance results from the 10×10-fold cross-validation were summarized as the mean for point estimates and the 2.5th and 97.5th percentiles for 95% confidence intervals (CIs).

さらに、臨床的な有用性の評価としてNRIを用いたとしています．ACC/AHAのガイドラインに掲載されているリスク閾値である7.5％と20%のところで区切る、カテゴリカルNRIを用いたとしています．

さらにこのNRIの信頼区間はBootstrappingで求めたということです．

4．予測値をStataで求める

予測確率を求めるのは、ノンパラメトリック法であれば前述の競合リスクを加味したCIFを用いて求める方法と、カプランマイヤーから求める方法があります．

Stataでは、CIFから求めるにはstsetしたあとに、

stcompet cif = ci, compet1(#)

といった形で求めます．

カプランマイヤーでは、これまたstsetしたあとに、

sts gen surv = s

こんな感じで求めておいて、これは生存関数なので、1から引けばイベント発生確率になります．

また、Cox回帰からの予測確率を求めるには、

stcox var1 var2 …

predict basesurv, basesurv

predict xb, xb

gen pcox = 1 – basesurv^exp(xb)

で求められます．手作業でcalibration plotをすることはできるのですが、これをもうちょっと簡単にやろうとすると、pmcalplotというコマンドが便利です．

しかしこれはstpm2というコマンドが例として載っているだけで、これだとスプライン関数を組み込んだ解析になるので正しいのかどうか、ちょっと自信が持てませんでした．(こちらのコマンドについては改めてまたしっかりとご紹介します)

この辺はまだまだRのほうがパッケージが充実してそうです．

今回の論文もSASとRを使ったと書かれてます．

Rのことはまったく詳しくないのですが、便利そうなパッケージを見つけましたので、詳しい人はこれでいいのかどうか、教えてください．

Index of prediction accuracy

nricens

コメント

タイトルとURLをコピーしました