slopepowerでサンプルサイズ計算をしよう！

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています． ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて、今回は混合効果モデルで推定したSlopeの効果を基にしたサンプルサイズの計算に使えるであろうコマンド”slopepower (st0647)”をご紹介します．

参考にした論文はこちらです．

Nash et al. Power and sample-size calculations for trials that compare slopes over time: Introducing the slopepower command. Stata Journal 2021: 21: 575-601.

通常のサンプルサイズ計算というのは、第一種の過誤、第二種の過誤を考慮に入れた、単純な数式で計算可能なわけですが、研究デザインや解析モデルによっては処置効果のばらつきを式に表すことが複雑な場合があり、そんな時に理にかなった方法が必要です．

近年、腎疾患領域では「死亡」や「腎代替療法の開始」といったハードアウトカムから、eGFRの30～40%減少であったり、あるいは年間低下率（eGFR slopeと呼びます）といった代理エンドポイントを使って処置効果を示すことが提唱されるようになってきました．

すでにいくつかの論文では腎代替療法導入に加えてeGFR slopeの群間差が有意であることをもって治療効果を示しています．

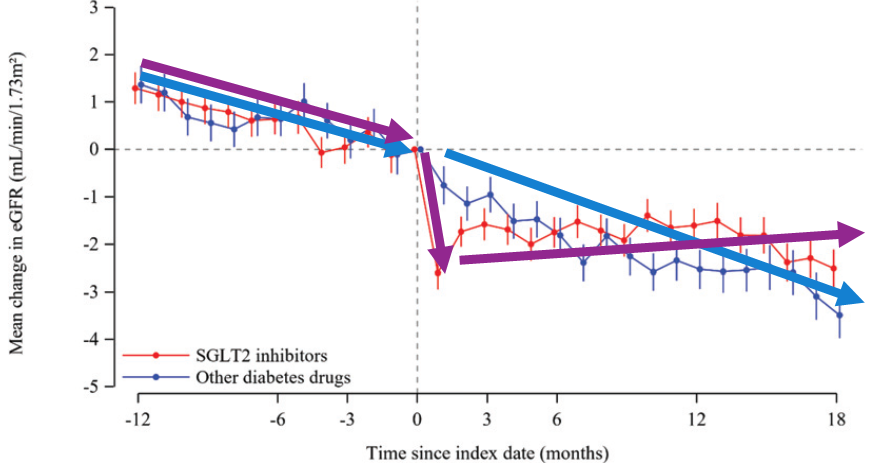
SGLT-2阻害薬の効果をeGFR slopeの違いで表現しています．

このように、従来のような０／１のアウトカムでもなければ連続変数での単純な平均値の比較でもないような解析手法を行うようなStudyにおいて、適切なサンプルサイズの設定を行うことは困難です．

ユーザー作成のコマンドでslopepowerというのがありましたので、それの使い方と、どんな場面で使えるか、考えてみました．

1．slopepowerの概要

難しい数式はなるべく使わないようにして概要を説明してみたいと思います．

適用される臨床試験

アウトカム変数が時間とともに変化し、処置に反応する連続的な値をとるようなparallel-armの試験に適用されるとしています．

Parallel-arm trial in which the outcome of interest is a continuous measurement of disease that is expected to change over time and to respond to treatment.

Slope計算のためのモデル

時間とともに変化するとはいっても完全にランダムな変化をするわけではなく、少なくとも個人においてはある程度そろった値をとりながら変化していきます．

つまり、一人一人の個人ごとの階層構造をとり、その中での値が相関しているという前提にあるわけです．こんなときに使えるのが混合効果モデルなのでした．(以前の記事)

このslopepowerというコマンドは、混合効果モデルで推定したSlopeをもとに、サンプルサイズを計算してくれる、という風に理解してください．

必要な情報

通常、サンプルサイズは、処置の有無で効果がどの程度異なるのか（＋それらのばらつき具合）を先行研究やパイロット研究のデータから得て、それらを基にして見積もることができます．

また、生存時間分析では研究デザインに関する情報も加味してサンプルサイズの計算を行うことができます．（以前の記事）

ところが、このslopepowerというプログラムは、点推定値やばらつき（分散など）、研究デザインに関する情報だけでなく、ある程度まとまったデータが必要になるようです．具体的には以下の2段階のステップで計算を行います．

もう少し詳しく解説してみましょう．

　

2．サンプルサイズ計算の2つのステップ

第一段階として、ユーザーが準備するデータの種類について説明します．これは、以下の3つのシナリオが想定されています

1. Single group
2. Two group, observational　（Healthy control）→Case-control
3. Two group, RCT

単一グループの検討では、何も治療を受けていない患者であったり、標準治療を受けているような患者が含まれているようなデータを使います．過去の観察研究やRCTのコントロール群からとってきたデータなどが想定されます．新しい治療を受けたら改善するような人達がいる、という潜在的な治療群です．

2つ目の、2群の観察データでは、疾患のない人達のデータを含んでいます.(case-control)　属性の異なる2群であるためにinterceptもslopeもそれぞれに持つことになります．

3つ目の、RCTのデータでは、疾患を持ち、追加的な治療を受けている人を含んでいます．（treated subjects）この場合はuntreated とtreated以外の条件がそろっているためにinterceptは共通となります．variance parameterも両群で同じになる想定です．

このように、3つの異なるシナリオをこのプログラムは用意しているとのことです．

　

第2段階としては、上記の3つのシナリオにおいて、どのような治療効果になるかを指定することです．

1．Single groupでは、年間変化率が0になる治療効果をもたらす介入が与えられた場合の状況を想定します．この状況では、サンプルサイズの計算で使用される目標治療効果は、ユーザー提供のデータから得られた傾きと、ユーザーが提供する任意の効果（effectiveness，0 から 1 の間の値をとる)から与えられます．

2．Case-controlの2群では、疾患群と健常群の効果差分（excess rate of change）としてデータから得られた傾きの差と、同じようにユーザーが指定する任意の治療効果から与えらえれます．

3．RCTの2群では、治療群と対照群の効果の差分、すなわち過去に観測された治療効果そのものをもってサンプルサイズを計算できます．これが一番シンプルでわかりやすいです．

　

3．slopepowerのsyntax

まずはslopepowerのプログラムをゲットしましょう．

help st0647

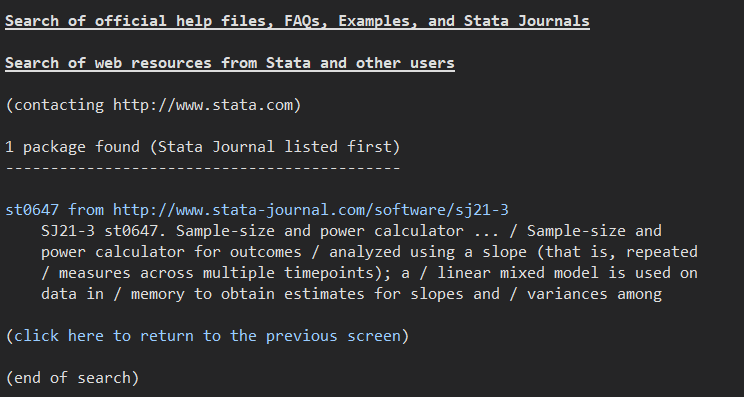
順番にクリックしていくことでインストールされますので、画面に従っていきましょう．

さて、無事にインストールできたら、ヘルプ画面をじっくり見てみましょう．

slopepower depvar [if] [in], subject(varname) time(varname)
schedule(numlist) {obs | rct} [nocontrols casecon(varname)
treat(varname) dropouts(numlist) scale(#) alpha(#) power(#) n(#) effectiveness(#) | usetrt] iterate(#) nocontvar]

ここで、上記3つのシナリオ別に理解していきましょう．

1．単群では、nocontrols, casecon(varname), treat(varname)のうちのnocontrolsをまず選択します．

2．Case-controlでは、caseconを選択して群分けするための変数名を（）の中に入れましょう．

3．RCTではtreatを選択し、群分けするための変数名を（）の中に入れましょう．

単群またはCase-controlではeffectivenessを指定します．デフォルトでは0.25、つまり、25％の人に効果がある、という風に勝手に指定してくれます．

RCTであればeffectivenessではなく、usetrtを選択します．

サンプルサイズ計算の場合にはpowerのところに検出力である0.8～0.9を入れ、検出力を調べたい場合には症例数をnに入れます．

ancillary fileにあるデータセット3つはそれぞれ上記3つのシナリオに対応していますが、自分たちで作ってもいいです．論文のAppendixに載っていますので、ご自身で試すことも可能です．

* Data for example 4.1: single-group data, untreated subjects only
set seed 5221
* create dataset of 200 people
clear
set obs 200
generate id = _n
* draw random person intercepts and slopes
drawnorm a b, cov(100, 5 \ 5, 2)
* create more visits
expand 4
by id, sort: generate visit = _n - 1
* generate sdmt from model in (7)
generate sdmt = 34 -1.8 * visit + a + b * visit + rnormal(0, 10^0.5)
summarize sdmt
count if sdmt < 0
* truncate at zero, and round to nearest integer to create a score like sdmt
replace sdmt = round(sdmt)
replace sdmt = 0 if sdmt < 0
* drop person intercept and slope, which are no longer needed
drop a b
save slpower1, replace

実はこのサンプルデータの創出におけるDo-fileにも様々な叡智が埋め込まれています．

せっかくなのでこれを利用してちょっとシミュレーションをやってみましょう．

4．シミュレーション

ここで、ちょっと応用編として、自分でデータを作ってみます．（かなり適当に作るので、あまり数値自体はあてにしないでくださいね！）

1か月ごとのVisitを参加者にしてもらって、その都度採血してもらってeGFRを測定します．

処置群と対照群との間で平均して年間で1.5くらいのeGFRの違いを生むような治療に対するRCTを行っているとしましょう．

* シードを設定
set seed 100
* 組み入れ患者は100名、そのうち処置群50名、対照群50名とする
clear
set obs 100
generate id = _n
generate treat = (_n > `=_N/2')
* 個人ごとのランダム切片とランダムslopeを適当に作りだす（この設定もサンプルサイズに結構影響します）
drawnorm a b, cov(100, 5 \ 5, 1)
replace a = a 
replace b = b 
* 月1回のvisitで合計12回来てもらう
expand 12
by id, sort: generate visit = _n - 1
* eGFR値を個人ごとにgenerateする
generate eGFR = 60 -0.12*visit - 0.12* treat * visit + a + b * visit + rnormal(0, 5^0.5)
* label treatment variable
label define treat_lab 0 "Placebo" 1 "Treat"
label values treat treat_lab
* 要らない変数は削除
drop a b
save slpower_original, replace

ここで処置群と対照群のeGFRの分布をみてみましょう．

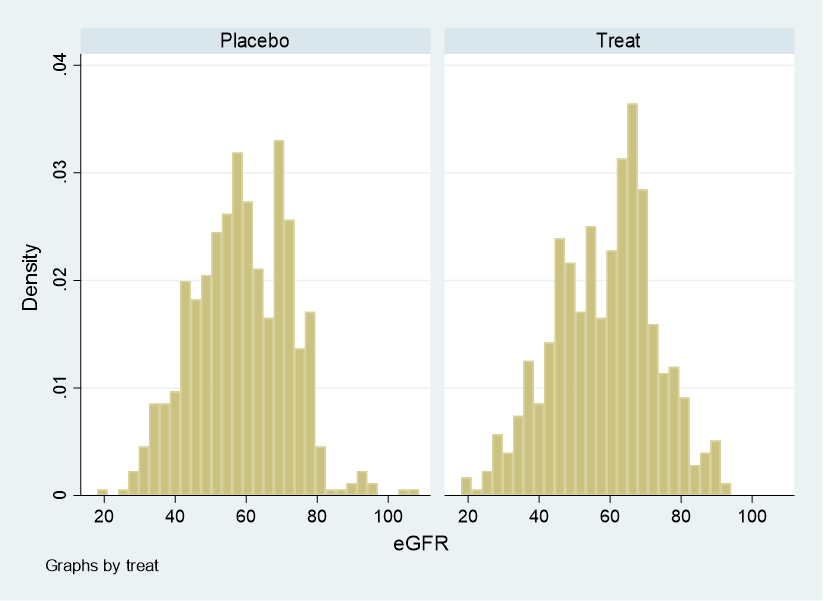
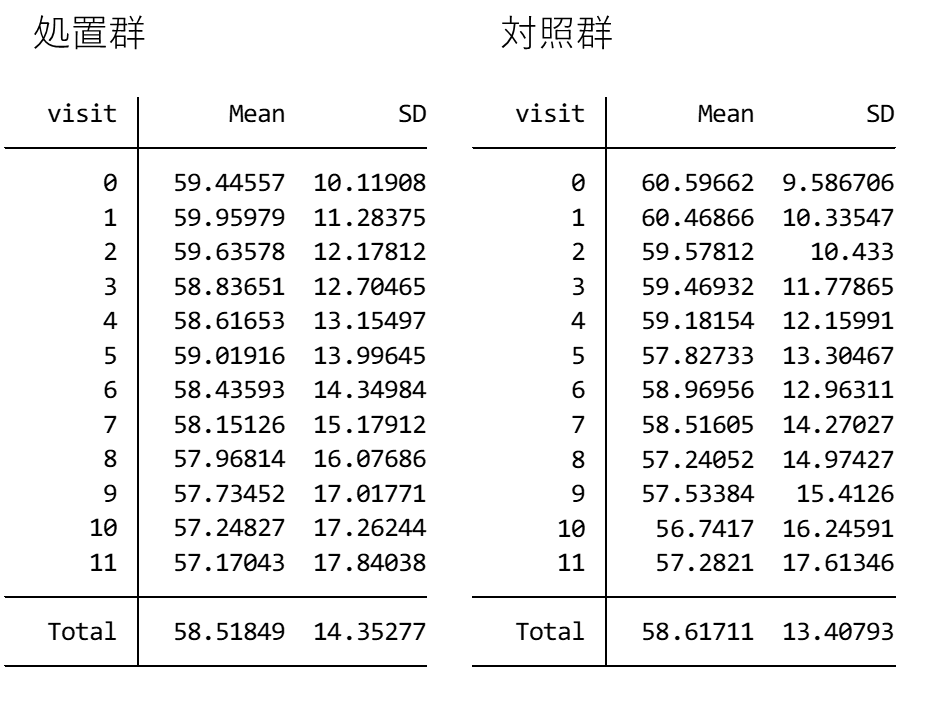
ここで3つのシナリオを考えてみましょう．

1. 月1回のvisitを1年間続ける
2. 3か月に1回のvisitを1年間続ける
3. 月1回を2年間続ける

これで必要なサンプルサイズを比較してみます．

なんとなく、

• slope評価は長いほどサンプルサイズが小さくて済むのではないか
• Visitの回数が頻回なほどサンプルサイズが小さくて済むのではないか

ということは直観的に予想できるのですが、その影響力がそれぞれどんなもんなのか、比べてみましょう．

* サンプルサイズ計算①月1回のvisitで有意差を生み出すための最小限のサンプルサイズ
slopepower eGFR, schedule(1(1)11)  subject(id) time(visit) rct treat(treat) usetrt
* サンプルサイズ計算②3か月ごとのvisitで有意差を生み出すための最小限のサンプルサイズ
slopepower eGFR, schedule(3 6 9)  subject(id) time(visit) rct treat(treat) usetrt
* サンプルサイズ計算③月1回のvisitを2年続ける場合の最小限のサンプルサイズ
slopepower eGFR, schedule(1(1)23)  subject(id) time(visit) rct treat(treat) usetrt

シナリオ①

両群のSlopeの差が0.126／月なので、大体年に直すと1.5くらいということになります．正直ここまでの治療効果を出すような薬剤はあまりなさそうです．先のSGLT-2阻害薬の例でも年間で0.75 mL/min/1.73 m2くらいの低下という感じでしたので、その2倍くらいの効果をもたらす薬剤ってことになります．

シナリオ②

シナリオ③

意外と2年間に延ばしてもそれほどサンプルサイズを減らすのに寄与しなさそうです．減らすには減らすのですけどね．まあSlope自体を推定するにはもうちょっと現実世界ではバラバラとした値だと思うので、もうちょっといいのではないかと思うのですが．

そしてvisitの回数を減らすとどうなるかというと、これは症例数が3割増しくらいになりそうです．

短い期間で終わらせたいのが臨床試験ですから、毎月来てもらうのがイイでしょうね．期間を延長して得られるメリットは今回の検証ではそれほど大きくはなさそうでした．

5．まとめ

いかがでしたでしょうか．観察されたデータセットが必要であること、それと、効果の差分を最初からは指定することはできないことなどがあり、なかなか使いづらいかなという風に感じました．（傾きゼロになる治療の効果が何パーセントの人で生じるか、という指定はなかなかイメージしにくいなと）

しかし、今回のシミュレーションのような形で、パイロット研究としての小さなRCTを実施した結果を使うことができるのであれば、使いようがあるかと思いました．

このあたりは自分の研究がもうちょっと進んでから改めて続報を掲載していきたいと思います．