このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回の記事は、予告通り(?)スプラインをxblcコマンド抜きで描いてみよう!というテーマで臨みたいと思います.
以前もxblc抜きでPoisson回帰により算出したincidence rateをスプラインで表現する方法をご紹介しました.
実はこのxblcコマンドのすごいところは、オッズ比やハザード比といった「比」を計算するときに結構トリッキーなことをしてのけていた、ということなのです.
ハザード比でもオッズ比でも、リファレンスカテゴリを指定する必要があります。そして、指定したリファレンスカテゴリーの値で割り算することで、ハザード比やオッズ比が求められます.
点推定値だけならば話は簡単なのですが、信頼区間があるので、単純に割り算すればよいというわけではありません.
ハザード比やオッズ比の元となる、ハザードやオッズですが、それぞれexp()の中の線形予測子が線形回帰の式になっています.
リファレンスカテゴリのハザードやオッズで割り算する際は、線形予測式の中では引き算になります.
数式はあまり出したくないのですが、こればっかりは式を見てもらった方がわかりやすいので、示します.
1.ロジスティック回帰
まずはロジスティック回帰モデルから考えてみましょう.
ロジスティック回帰は確率piのロジット(logit)、対数オッズ(log odds) が線形予測式で表現される、という前提です.式にするとこんな感じ.この左辺がロジットとか対数オッズとかいうものです.
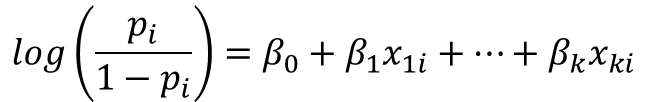
i=1,2,…,nのサンプルに対して、イベントが起こる確率pi(サンプルごとに起こる確率が違う)が、説明変数によって予測あるいは説明しようというのがロジスティック回帰の本質です.
何でこんな回りくどいことをしているのかというと、もし左辺が確率だとすると、0から1までの値しか取りえないために使いづらいからです.ロジットにすることで連続的な値になりますので、使いやすいってことですね.
ところで、ロジスティック回帰分析の最終結果は、オッズ比で表現されることが多いですよね.これはオッズとオッズの比、つまり割り算したものがオッズ比になります.
最も簡単な例として、1つの変数x1について、それが1だけ上がったときの確率をq、元の確率をpとして、オッズ比を求めてみましょう.
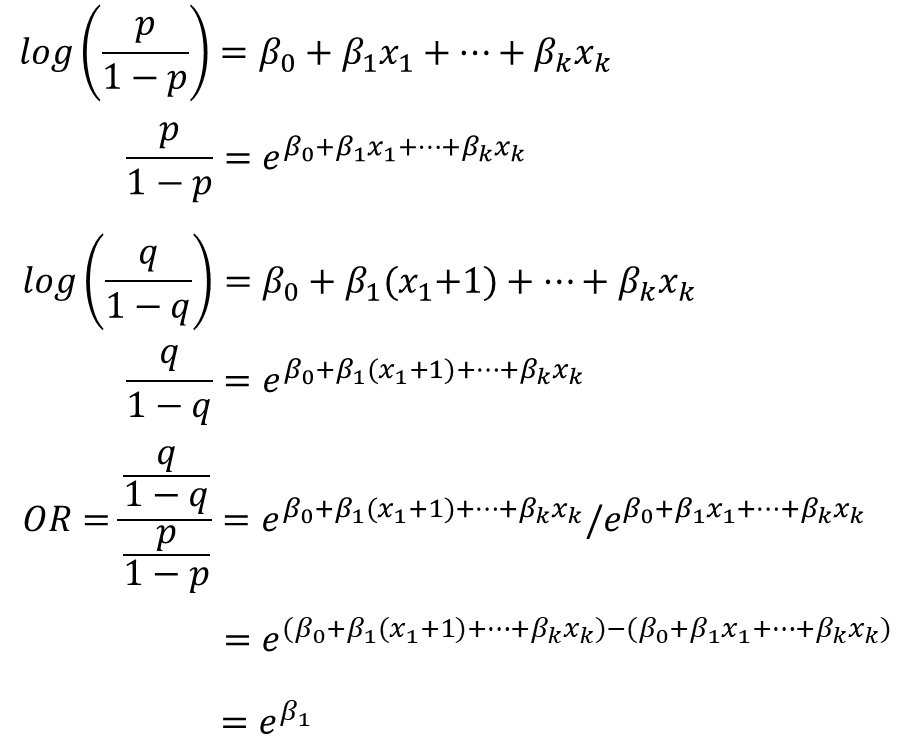
指数の割り算はべき乗数の引き算になりますので、こんな感じですっきりします.
2.スプラインでオッズ比を算出する
スプラインの場合も、ある曝露因子を連続的に変化させたときに、参照基準におけるオッズと比較して何倍になるのかを見ますので、基本的な考え方としては上記の式を基に考えればよいです.
mkspline rcs_idpvar = idpvar, cubic nknot(3)このように入れると、rcs_idpvar1とrcs_idpvar2という新しい変数が誕生します.
これはそのままでは解読不能なのですが、3次関数の曲線を描くためにいい感じに設定された変数だと思っておきましょう.
logistic depvar rcs_idpvar1 rcs_idpvar2 cov1 cov2…これだけでは残念ながらリファレンスを表現することができません.これをどのように解決するのかを考えてみます.
下の数式はx1をxaとxbの2つの変数に分けたところと考えてください.
リファレンスの位置の rcs_idpvar1, rcs_idpvar2の値はそれぞれxar, xbrとなります.
それをそれぞれxa, xbから引き算すればリファレンスの値を引いた対数オッズ比が出てくるはずです.

引き算した後のスプライン変数をrcs_idpvar1’ rcs_idpvar2’ などとして
係数はそのままにして説明変数 としてそのまま入れて計算させればオッズ比がそれぞれ算出されるというわけです.
3. オッズ比を信頼区間付きで算出する
次に、オッズ比を信頼区間付きで算出する手順を説明していきます.
ここで便利な関数コマンド“predictnl”が出てきます.
ロジスティック回帰分析を終えた後に、predictnlの関数を使えば対数オッズを信頼区間付きで計算してくれます.
これははっきり言ってかなり便利です.
(※でも、これ、対数オッズなんですよ.オッズ比じゃないんです.だからこんなにややこしいことをやってきたわけです.)
predictnl yhat = _b[rcs_idpvar1]*rcs_idpvar1’ + _b[rcs_idpvar2]*rcs_idpvar2’ , ci(lb ub) level(95)(※lb=lower boundary, ub = upper boundaryのつもり)
あとはyhat, lb, ubをexponentすればOKです。
4.これができるとどんないいことが?+サンプルコード
これができると、
- 多重代入後のデータセットでも同じことができる
- 複数の群に分けてスプラインを描くときに自由自在にリファレンスを設定できる
というとてつもないメリットがあります。これはxblcではなし得ません.
最後にサンプルコードを示します。上記の解説を踏まえて一つ一つのステップを確認してみてください.
1)xblcで実行するパターン
webuse lbw, clear
mkspline2 rcs_lwt = lwt, cubic nknot(3) dis
logit low rcs_lwt* smoke ptl ht
levelsof lwt , local(levels)
xblc rcs_lwt*, covname(lwt) at(`r(levels)') reference(100) eform gen(pt or lb ub)
#delimit;
twoway
(line or pt , lc(maroon) lp(solid) lw(medthick) yline(1, lpattern(dash) lcolor(black)) sort yaxis(1))
||
(line lb pt, lw(medthick) lc(maroon) lp(shortdash) sort yaxis(1))
||
(line ub pt, lw(medthick) lc(maroon) lp(shortdash) sort yaxis(1))
,
ytitle("Odds Ratios") xtitle("lwt") legend(off) graphregion(color(white)) ylabel(, ang(0)) ysca(log)
;
#delimit cr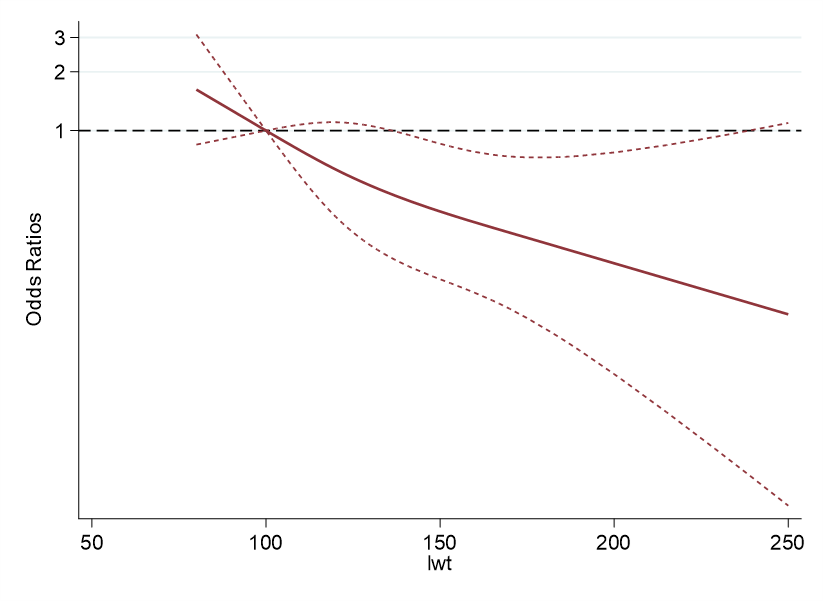
2)手作りプログラムで作成した場合
webuse lbw, clear
mkspline2 rcs_lwt = lwt, cubic nknot(3) dis
sort lwt
scalar lwt_ref = 100
gen flg_ref = 1 if lwt >= lwt_ref
sort flg_ref lwt
scalar rcs_ref1 = rcs_lwt1 in 1
scalar rcs_ref2 = rcs_lwt2 in 1
logit low rcs_lwt* smoke ptl ht
replace rcs_lwt1 = rcs_lwt1 - rcs_ref1
replace rcs_lwt2 = rcs_lwt2 - rcs_ref2
predictnl yhat = _b[rcs_lwt1]*rcs_lwt1 + _b[rcs_lwt2]*rcs_lwt2, ci(lb ub) level(95)
gen or = exp(yhat)
replace lb = exp(lb)
replace ub = exp(ub)
sort lwt
#delimit;
twoway
(line or lwt , lc(maroon) lp(solid) lw(medthick) yline(1, lpattern(dash) lcolor(black)) sort yaxis(1))
||
(line lb lwt, lw(medthick) lc(maroon) lp(shortdash) sort yaxis(1))
||
(line ub lwt, lw(medthick) lc(maroon) lp(shortdash) sort yaxis(1))
,
ytitle("Odds Ratios") xtitle("lwt") legend(off) graphregion(color(white)) ylabel(, ang(0)) ysca(log)
;
#delimit cr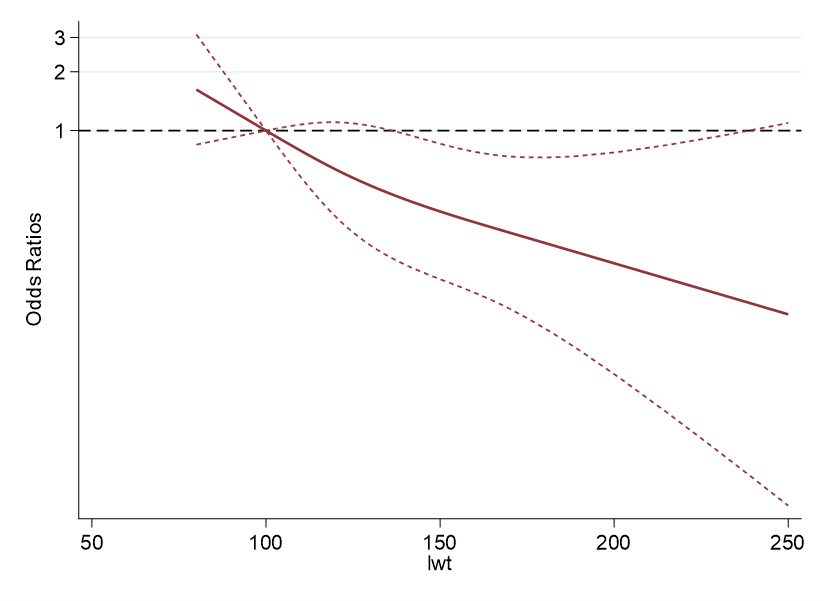
ということでピッタリ合致しました.
多重代入の際にはpredictnlの前にmiをつけてくださいね!
こちらについてもおいおい記事をかけたらまとめてみたいと思います.



コメント
[…] さて、前回に引き続き、スプラインをxblcコマンド抜きで描いてみよう!というテーマで、今回は生存時間分析によく使われるCox比例ハザードモデルに実装してみたいと思います. […]