このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回は、非線形の関係にある、連続的な曝露因子に対するIncidence rateを滑らかに表現する方法(スプライン)を示してみたいと思います.
今回の記事を作成するにあたって最初に見た論文がこちら.
Teerlink et al. Effect of Ejection Fraction on Clinical Outcomes in Patients Treated With Omecamtiv Mecarbil in GALACTIC-HF. JACC 2021;78:97-108
で、Central illustrationとして描かれていたFigureに興味を持ったからでした.
縦軸をincidence rateとし、横軸は連続値.そして関連は非線形、ということで使い勝手がよさそうです.
しかもよく見れば、このincidence rateを出すのに何やらPoisson regressionを使ったとあるじゃありませんか!謎に満ちていたので、ちょっとやり方をしらべてみました.
1.データセット(オリジナル)の準備
非常に簡単ながら、データセットを用意しておきました.もはやこの手のでたらめなデータセットを作るのは大得意となってしまいましたが、くれぐれも悪用しないでくださいね.間違っても論文投稿などしないようにお願いします.(そんな人いないか…)
さて、データセットです.自己責任でダウンロードお願いします.
これを展開していただくと、771レコードほどのデータが入っていて、case, age, sex, exposure, outcome, year という変数が格納されているので、ご確認ください.
caseとは通し番号で、IDみたいなものです.年齢、性別、曝露因子、アウトカム(0/1)とイベントまでの時間(年)となっています.
2.Poissonでincidence rate ratioを計算する
次に、解析の中心となる、Incidence rateの計算ですが、その前にPoisson回帰でよく求める、Incidence rate ratioを先に求めてみましょう.
import excel using "poisson_rcs.xlsx", firstrow clear
poisson outcome age sex exposure, exposure(year) irr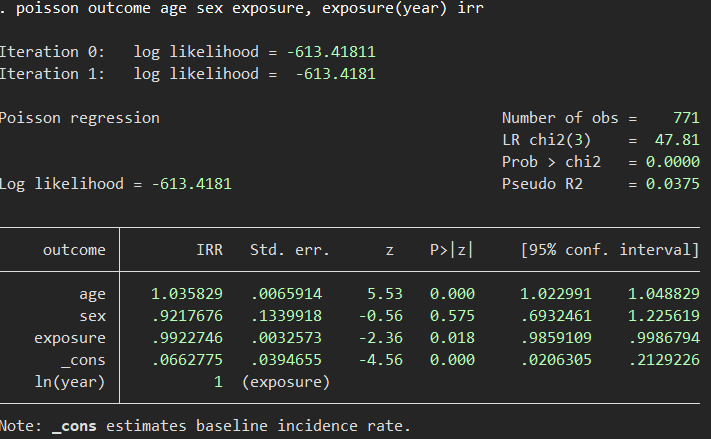
こんな感じでやることが多いと思います.これをスプラインで表現するとどうなるかが次です.
3.スプラインでIncidence rateを表現する
今度はスプラインを描きたいと思います.最初にノットの数を指定しますが、今回は単純に、3つとしてみますね.
そして、最終的に、incidence rateを100人年あたりで表現したいので、時間(年)を100で割っておきます.
import excel using "poisson_rcs.xlsx", firstrow clear
mkspline index = exposure, cubic nknots(3)
gen time = year/100
poisson outcome age sex index* , exposure(time)このあとは、信頼区間付きでincidence rateを計算するため、Post estimateとして、predictnl コマンドを使用します.
また、Predictするにあたって、covariateすべてに、そのコホートの平均値を入れ替えてください.この作業をしないと一つのグラフになりません.
foreach v of varlist age sex {
sum `v'
replace `v' = r(mean)
}
predictnl ir = predict(ir), ci(lb ub) /* 2022/4/11 訂正 */
predictnl ir = xb(), ci(lb ub) /* 2022/4/11 追記 */
replace ir = exp(ir)
replace lb = exp(lb)
replace ub = exp(ub)(注釈)上記のプログラムを訂正しました。信頼区間がxblcと若干ずれるのが気になっていたのですが、irを直接predict関数で求めるのではなく、xbで対数値で取り出した後に、exponentしたほうが正確になるようです.時々incidence rateがマイナスの値をとってしまうことがあったりして、あまりよい方法ではなかったようです。今回訂正した方法では無事解決されておりました.
このPredictする前の平均への置き換えがなかなか理解されないのですが、しょせんはRCSというのはその集団における代表的な人がExposureだけを変えるとリスクがどんな風に変化するかを見たいだけのものである、ということが根底にあります.
それでも理解できない場合は、そうしないとこうなる、ということだけご理解ください.
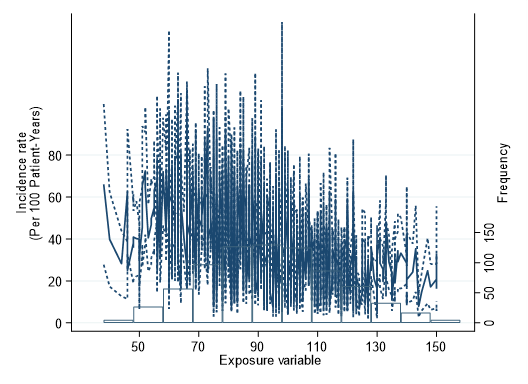
そして無事にPredictができたらtwowayでグラフを描きましょう.incidence rate, 信頼区間、そしてヒストグラムを重ねてみました.
#delimit;
twoway
(line ir exposure, lc(navy) lp(solid) lw(medthick) sort yaxis(1))
||
(line lb exposure, lw(medthick) lc(navy) lp(shortdash) sort yaxis(1))
||
(line ub exposure, lw(medthick) lc(navy) lp(shortdash) sort yaxis(1))
||
(hist exposure, freq fcolor(none) lcolor(edkblue) w(10) lw(thin) yaxis(2))
,
ytitle("Incidence rate" "(Per 100 Patient-Years)") xtitle("Exposure variable")
xscale(range(30 160)) xlabel(50(20)150)
yscale(range(10 80)) ylabel(0(20)80, ang(0))
ylabel(0 50 100 150, axis(2)) ysc(range(0 500) axis(2))
legend(off) graphregion(color(white))
;
#delimit cr そして最後にこんな風にできれば完成です.
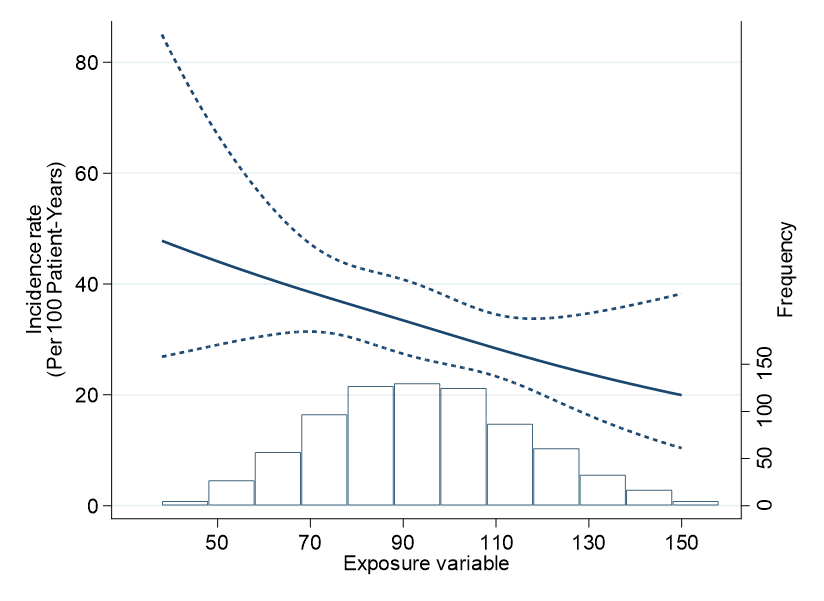
ちなみに、
predictnl ir = predict(ir), ci(lb ub)
で作図すると、信頼区間が微妙にずれます.
xblcコマンドとの整合性についても確認をしてみましたが、predictで一発で求めるよりも、まずxbで対数値を求めた後にexponentiateしたほうがよさそうです.ぴったりと結果が重なりました
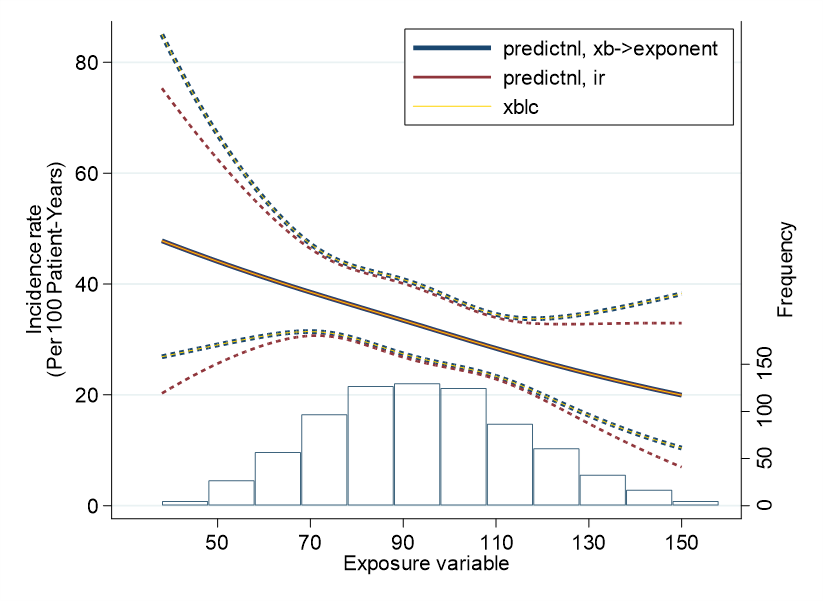
Remark on the manipulability of nonlinear Wald tests
In contrast to likelihood-ratio tests, different — mathematically equivalent — formulations of an hypothesis may lead to different results for a nonlinear Wald test (lack of invariance). For instance, the two hypotheses
H0: pnl_exp[i] = 0
H0: exp(pnl_exp[i]) – 1 = 0
are mathematically equivalent expressions but do not yield the same test statistic and p-value. In extreme cases, under one formulation, one would reject H0, whereas under an equivalent formulation one would not reject H0.
“predictnl”コマンドヘルプより
これだけ読んでもよくわかりませんが、とにかく計算の仕方が違うことは確かなようです.
xblcで作成したコマンドはコチラです.共変量の中心化は必須です.
foreach v of varlist age sex {
sum `v'
replace `v' = `v' - r(mean)
}
poisson outcome age sex index* , exposure(time)
levelsof exposure, local(levels)
qui xblc index*, covname(exposure) at(`levels') eform line gen(pa ir lb ub)
#delimit;
twoway
(line ir pa, lc(navy) lp(solid) lw(medthick) sort yaxis(1))
||
(line lb pa, lw(medthick) lc(navy) lp(shortdash) sort yaxis(1))
||
(line ub pa, lw(medthick) lc(navy) lp(shortdash) sort yaxis(1))
||
(hist exposure, freq fcolor(none) lcolor(edkblue) w(10) lw(thin) yaxis(2))
,
ytitle("Incidence rate" "(Per 100 Patient-Years)") xtitle("Exposure variable")
xscale(range(30 160)) xlabel(50(20)150)
yscale(range(10 80)) ylabel(0(20)80, ang(0))
ylabel(0 50 100 150, axis(2)) ysc(range(0 500) axis(2))
legend(off) graphregion(color(white))
;
#delimit cr 一方で、今回記載したやり方については、中心化よりも、その後共変量をすべて平均値に置き換えるという作業が重要です.最初に中心化した場合には平均値=0ですので、すべての共変量(興味のあるexposure, outcome, splineのための変数以外)は0に置き換えれば平均値になります.
最初に中心化してなければ、r(mean)をsumのあとに取り出して置き換えればOKです.
まとめ
Poisson regressionからIncidence rateのスプラインを描いてみました.臨床で通常我々が経験するものは、どれも大抵は「珍しいアウトカム」ですから、ほぼどんな場合にも適用可能と考えます.
ここで、RCSのコマンド・プログラムにおける共変量の扱いについて、ポイントをわかりやすくまとめると、
xblcあり→回帰分析前に共変量を平均値で引く(センタリング)→ xblc前は操作不要(xblcが共変量を揃えてくれる)
xblcなし→回帰分析前は操作不要(センタリングしてもいい)→predictnl前に全て平均値に(センタリングしている場合には0に)揃える
ということになりますね.



コメント
[…] 以前もxblc抜きでPoisson回帰により算出したincidence rateをスプラインで表現する方法をご紹介しました. […]
[…] Poisson回帰によるincidence rateのスプラインはこちら […]