このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回はクロス表における独立性の検定(χ2検定)についてまとめてみたいと思います.
ある2つのカテゴリ変数である要素Aと要素Bの関係性を表にまとめるとき、その表を分割表(Contingency table)とか、クロス表(cross table)あるいはtwo-way tableなどと呼びます.
そして、それらの要素が互いに独立したものであるのかどうかを検定するのがχ2検定です.
クロス表の基本的な要素とχ2検定のやり方を数式とStataのコマンドやプログラムを使って解説してみたいと思います.
1.クロス表の基本
今更ですが、クロス表の基本的な要素について解説してみたいと思います.

要素A, Bに関するクロス表ですが、まずは簡単な用語を整理しておきます.
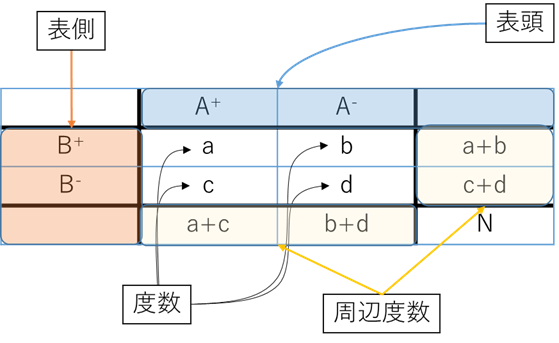
どちらを表頭・表側にするかについての明確な決まりはありませんが、Exposureを表側にしてOutcomeを表頭にすることが多いです.
なのでその順番に従っておく方が覚えやすいと思います.感度・特異度、陽性的中率・陰性的中率などの計算を行うときに常に決まりが一定しているほうが間違えないですよね.
Exposureの”E“の字が、表の横の枠に見えてきますね.それをもとにして自分は無理やり覚えました.また、感度特異度の計算は縦方向で行います.(感度がP(B+|A+)、特異度がP(B–|A–)でしたね!)
感度 → 感動して涙を流す → 涙は縦方向に流れる、ということで計算を縦方向で行う.
という覚え方をしているのですが、「これでいつも思い出せます!」と言ってもらえたことがある(n=1)ので、役に立つかもしれません.
周辺度数ですが、これはχ2検定のときに使う数字です.日本語で「周辺」と使われているのがとても分かりにくいといつも思っているのですが、英語で言えばmarginで、確かにこの表でいえばマージンにあるなあと妙に納得してしまいます.
2.χ2検定による独立性の検定
上記のクロス表の2要素A,Bが独立しているかどうかを検討するために、χ2検定を行います.
要素A,Bはともに二値変数として行いますが、カテゴリが3つ以上になってもχ2検定は使うことができます.
χ2検定で行いたい検定というのは、「Aの割合がBの状況によらず一定である」という帰無仮説を棄却することです.
χ2検定においては、「期待度数」というものをまずは求めます.
期待度数は周辺度数から計算します.

ここで合計人数をNとします.A+かつB+という条件を満たすのは、(a+b)/N × (a+c)/N × Nで計算されますので、縦方向と横方向の周辺度数の積を全体の母数で割ったものになります.
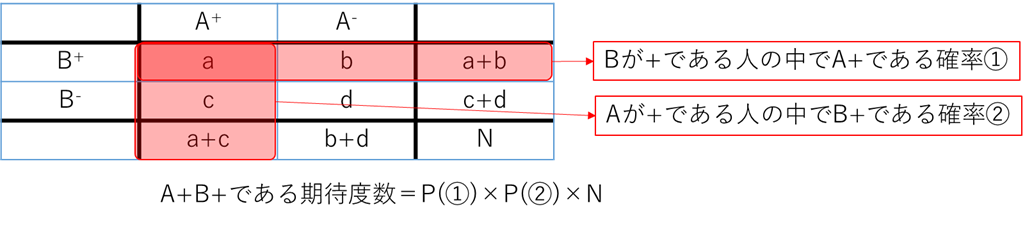
そして各セルの観測度数a, b, c, dが、同じ行の周辺度数と同じ列の周辺度数から計算された期待度数とどのくらい違うのか、という値が検定統計量となります.
もっと正確に書くと、「各セルの観測度数と期待度数の差の二乗」を「そのセルの期待度数で割って」すべてのセルで足したもの、が検定統計量であるχ2値です.
ここで、χ2検定を行うためには以下の前提を満たしている必要があります.
- データがそれぞれに独立している
- 期待度数(expected cell counts)≧5
- セルが増えた場合は期待度数5未満のセルが全体の20%以下
期待度数が少ないときにはFisher’s exact testを行います.
χ2分布の統計量を検討する場合、自由度を指定する必要があります.各要素のカテゴリ数ー1の合計となりますので、2×2の表の場合は自由度は1となります.
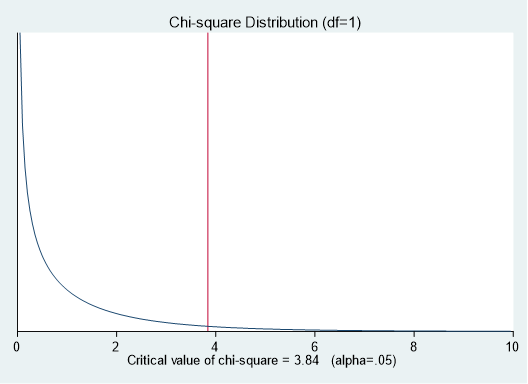
確率密度関数がχ2分布になることから、曲線下面積は合計で1となります.赤線よりも右の曲線下面積が0.05となるところを有意水準(critical value)として、自由度1では3.84と求められます.
ちなみに上記曲線は、自由度1、有意水準α=0.05とした場合に以下のプログラム
local df= 1
local alpha = .05
local xsqr = invchi2tail(`df',`alpha')
local nu = `df'/2
range x 0 10
generate chi2 = (x^(`nu'-1)*exp(-1*x/2))/((2^(`nu'))*exp(lngamma(`nu')))
local xtitle = "Critical value of chi-square = " + string(round(`xsqr',.01)) + " (alpha=`alpha')"
graph twoway scatter chi2 x if x<10 , s(i) c(l) ///
xline(0, lcolor(gs1)) xscale(noline) xline(`xsqr') ///
yline(0, lcolor(gs1)) ylabel(none) yscale(noline) ///
t1("Chi-square Distribution (df=`df')") xtitle(`xtitle') ytitle("")で描くことができますのでお試しください.
.display invchi2tail(df, 0.05)
と入れていただくと、有意水準がわかります.(3.8414588)
Stataではtabulateコマンドにchi2というオプションをつければ簡単にP値が求められます.
sysuse auto, clear
gen expensive = price>5000
tab expensive foreign, chi2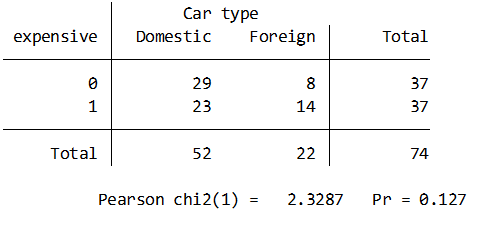
まあ手計算すれば以下のようになるんですけどね.誰もやらないと思いますが…
local ex1 = 52*37/74
local ex2 = 22*37/74
local ex3 = 52*37/74
local ex4 = 22*37/74
local x = ((`ex1' - 29)^2)/`ex1' + ((`ex2' - 8)^2)/`ex2' + ((`ex3' - 23)^2)/`ex3' + ((`ex4' - 14)^2)/`ex4'
display 1 - chi2(1, `x')3.母比率の検定でも求められる(別解)
2標本の割合の検定という概念を使えばχ2検定を使わなくても実施可能です.
prtestというコマンドがありますので、それを使って以下のように求められます.
sysuse auto, clear
gen expensive = price>5000
prtest expensive, by(foreign)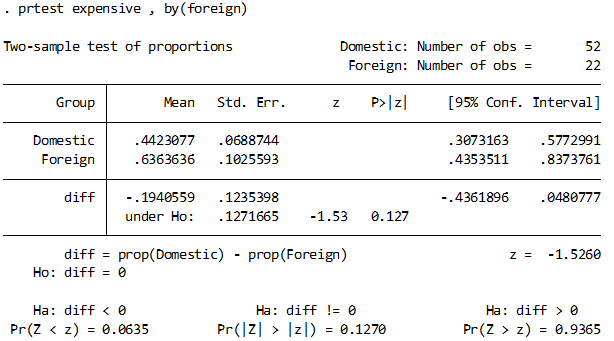
両側検定の結果0.120となっています.これは標本の割合が、同じ施行を繰り返すことである値に収束してくる、という性質(中心極限定理)を利用したものが考えの根底にあります.
標本比率は帰無仮説の下、標本平均(π0)とサンプル数(n)を用いて
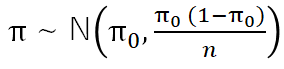
の正規分布に従います.
ここで、二つの要素expensive, foreignについて考える必要がありますので、それぞれの要素の比率が違わない、という帰無仮説を検証します.
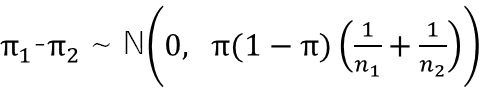
πはそれぞれの標本の加重平均を求めます.このときに正規分布に従うことを考えて、Z値を求めます.
なお、余談ではありますが、割合を記述するだけのはずのデータでなぜか信頼区間があるのを見て不思議に思ったことはないでしょうか?
これは先に出てきたように二項分布でも中心極限定理によって求められる母比率は幅をもって推定されうる、ということを考えればそれほど受け入れがたくはないかなと思います.
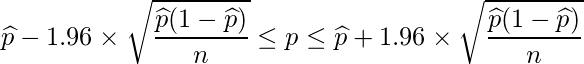
検討している症例数に依存することがわかります.すなわち症例数が多いほど信頼区間幅は狭くなり、得られた標本から推定される値が真の母比率を含む範囲が狭まることになります.
まとめ
分割表と割合の検定についてまとめました.
最近ベーシックな部分を復習していますが、新たな発見もあるのでたまにはいいかなと思っています.



コメント