一元配置分散分析をマニュアルでやってみる

統計

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています． ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて、今回も統計学に関する記事になります.

以前の記事で独立した2群間での連続変数の平均値の検定をt検定で行いました．

今回は3つ以上の集団における母平均の比較を行う方法についてみてみましょう．

3つ以上の母平均を比較するには、「分散分析」という方法が必要になります．

1．分散分析について

ところでこの分散分析には、一元配置分散分析（One-way Analysis of Variance）と二元配置分散分析（Two-way Analysis of Variance）があります.

この2つを理解するためには、「要因(factor)」と「水準(level)」を理解する必要があります．

まず、「要因」ですが、これは何らかの結果に影響を与える因子のことを指します．独立変数とか説明変数といった呼び方になります．

そして「水準」は、要因の中の異なる条件や種類のことを言います.

例えば、高血圧症の人たちに何らかの降圧薬を投与する研究が行われたとすると、降圧薬投与が要因であり、その種類が水準になります．プラセボと試験薬A、試験薬Bみたいな感じです．水準＝群として理解してください．

一元配置分散分析は、「3つ以上水準の母平均の差を検定する」方法であり、1つの要因のみを検討します．これに対して二元配置分散分析は、「2つの要因を含むデータから、各要因における水準間の平均値の差を検定する」方法です．

そもそも、分散分析とはいったい何をしているのでしょうか？なぜ「分散」を分析しなければいけないのでしょうか？平均値の比較なのに．

このような疑問を持たれた人は少なくないと思います．

データのばらつき具合を水準同士で比較したときに、水準間のばらつき度合いが各水準内でのばらつき(誤差変動)よりも大きければ、水準同士の効果が異なるだろう、ということを示そうとしています．

なので、そのばらつき方が水準間で大きく異なってしまってはうまくないわけです．

ということで、一元配置分散分析を行う際の前提条件は以下の通りになります．

  1. データは連続変数である
  2. 標本は母集団からランダムに抽出された独立したデータである
  3. データの分布は正規分布である
  4. 各群の分散は等しい（等分散性）

2．一元配置分散分析の流れ

まず、一元配置分散分析の帰無仮説は何でしょうか？

群が3つあるとして、それぞれの群における母平均をµ1, µ2, µ3としたとき、すべての群における母平均が同じであることが帰無仮説になります．

H0: µ1 ＝ µ2＝ µ3

その反対に、対立仮説は、少なくとも一つの群の母平均が他の母平均と異なることになります．

つまり、「要因による変動」が「誤差による変動」で説明がついてしまうのであれば帰無仮説が採択されることになります．

そこで、ANOVAを行う際には、まずデータのばらつき自体を「要因による変動」と「誤差による変動」に分けることから始めます．

以下にANOVAの手順を示します．

  1. 全データの平均を求める
  2. 要因による変動(between group sum of squares: BSS)を求める
  3. 誤差による変動(within group sum of squares: WSS)を求める
  4. 自由度を求める
  5. 検定統計量Fを求める
  6. 臨界値と比較する

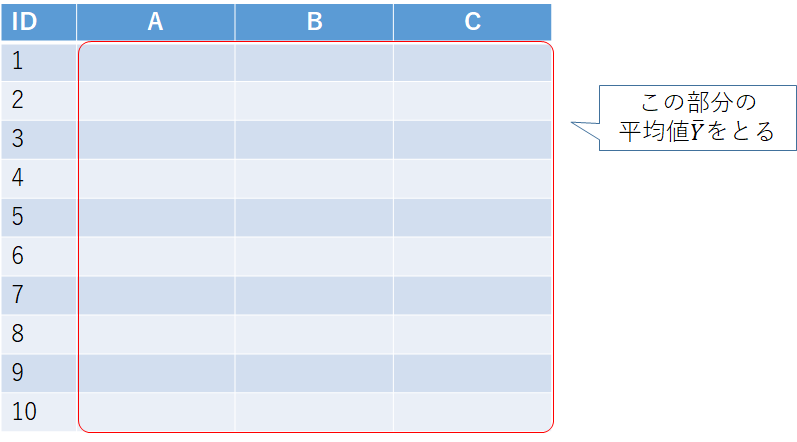
1．全データ平均を求める

これは単純に全部の値を足し算してnで割り算するだけです．

2．要因による変動(between group sum of squares: BSS)を求める

次に群間の変動を計算します．これは各群の平均と全平均の差の2乗を足し合わせていきます．

すべてのデータで足し合わせることになるので、各水準における標本数をかけて足し合わせることになりますので注意しましょう．

3．誤差による変動(within group sum of squares: WSS)を求める

次は個々のデータが属している群の平均とどの程度かけ離れているかを足し合わせていきます．

4．自由度を求める

自由度は比較する群の数とトータルの症例数によって決まります．群間変動(BSS)の自由度は比較する群の数-1で、群内変動(WSS)の自由度はすべてのデータ数-群の数で表されます．

5．検定統計量Fを求める

そして求まった自由度でそれぞれBSS、WSSを割って平均平方（mean square: MS）を計算し、比をとったものが検定統計量であるF値となります．

F ＝群間変動の平均変動　÷　群内変動の平均変動

で与えられます．感覚的に、群同士で大きくかけ離れているほうがF値が大きくなるのがわかると思います．F値が2つの自由度の組み合わせによって求められた臨界値を超えるかどうかで検定結果が決まります．

この表をそのまま覚えてしまうのが一番早いでしょうね.

6．臨界値と比較する

BSS、WSSそれぞれの自由度で割った平均平方の比であるF値と、下表のような構造の臨界点を比較することで検定が行えます．

↓v2　　v1→123
10
20
30

3．具体的なデータを使ってStataで試してみる

ということで、次のデータセットを使って実際にやってみましょう．

ckdsampleダウンロード

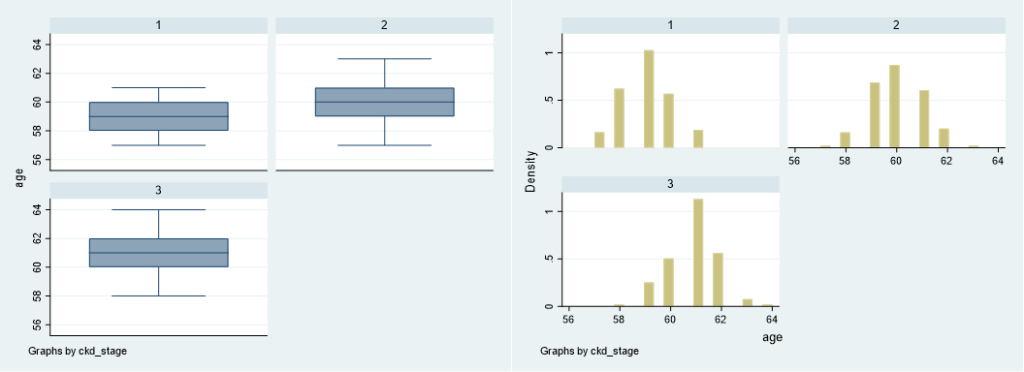
最初にANOVAの前提を確認します．分散が等しいかどうかについてはヒストグラムやBox plotなどの視覚的な確認をすることでたいていは大丈夫です．

*summary stat
bysort ckd_stage:sum age
*box plot
graph box age, by(ckd_stage)
*histogram
hist age, by(ckd_stage)
*qqnorm plot
qnorm age if ckd_stage==1
qnorm age if ckd_stage==2
qnorm age if ckd_stage==3
まあ、大体同じような分布の形になっていますかね…

いよいよANOVAになりますが、oneway, anovaと2つのコマンドが用意されています.

どちらも同じ答えになります．

oneway age ckd, tabulate

*alternative
anova age ckd_stage

こちらのほうが先ほどの表と配置も共通しているのでわかりやすいですね．

F値が有意かどうかは、Ftailという関数で直接検定できます．また、有意になるためのF値を自由度と有意水準から求めることもできます(invFtail)．

disp Ftail(2,351,88.96)
** 5.578e-32
disp invFtail(2,351,0.05)
** 3.0214465

まとめ

一元配置分散分析についてまとめてみました．ここで出てくるF値、F検定は次に出てくるであろう線形回帰でも重要な役割を負いますので、しっかり押さえておくとよいでしょう．

ちなみにこの記事って公衆衛生大学院の初年度の授業とかで習うんですかね．Stataを使うとよりなじみがでるのでお勧めです．

コメント

タイトルとURLをコピーしました