このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回は生存時間分析において頻用されるCox比例ハザードモデルの、様々な残差についてまとめてみました.なお、本記事は下記の書籍を参考にしました.これはマジで買いです.現在何回目かの通読にチャレンジしていますが、読み返すたびに新しい発見があります.
Cox比例ハザードモデルの残差は以下のようにいくつかありますが、それぞれに使い分けが存在します.
- Cox-Snell残差:Overall model fit、つまりモデルの当てはまりを調べるのに使える
- Martingale残差:共変量のfunctional formを決めるのに使える(対数変換するかどうか)
- Schoenfeld残差:比例ハザード性の確認、外れ値の影響力解析など
- Deviance(逸脱)残差:モデルの正確性や外れ値の同定
これらの残差はCox回帰を走らせたあとにpredictすることで得られます.
stcoxのhelp画面からpostestimationのリンクをたどって行きついたpredictを選択すると、こちらのような一覧が見つけることができます.実際にはpredict newvar, optionとして新しい変数を指定しながらオプションで必要な残差について指定すればよいわけです.
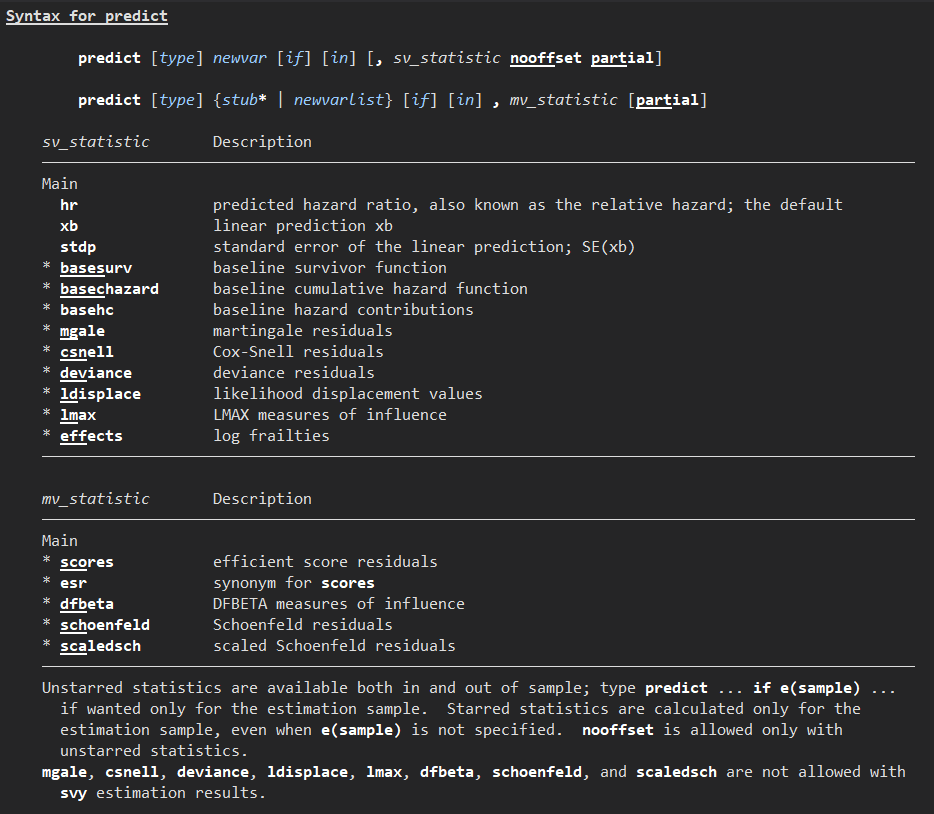
ここからは具体的なデータをみることにします.
use http://www.stata-press.com/data/cggm3/reyes, clear
describe
stsetこのように入力していただくと、生存時間分析のセッティングを確認できます.
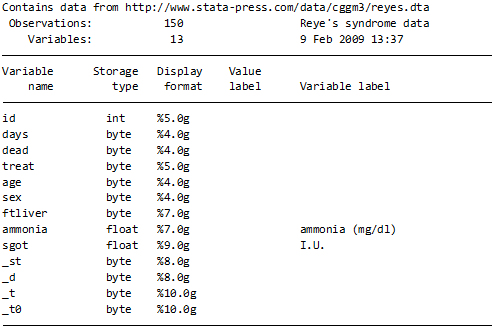

このデータセットで、変数の変形が必要かどうか、モデル全体の適合性はどうか、外れ値の影響はどうかについて検証してみたいと思います.(比例ハザード性についてはこちらにまとめています)
1.変数の変形が必要か?
線形回帰では、連続変数を入れるときに正規分布しているかどうかを確認していたかもしれません.これは本来は直接的には線形回帰の前提条件とは関係ありません.
正確に言えば、残差が正規分布しているかどうかが重要なのであって、変数そのものの正規性は問われないはずです.そしてその前提がクリアされていればその変数の分布がどのようなものであっても中心極限定理によって正当化されます.
同じようなことがこのCox回帰においても成立すると考えていただくとわかりやすいと思います.
さて、もとのデータセットに話を戻します.このデータセットにおいて、ammoniaという変数は、histogramを書いていただくとかなりright-skewedなデータになっています.そこで、Martingale残差を確認してみましょう.
stcox, estimate
predict mg, mgale
lowess mg ammonia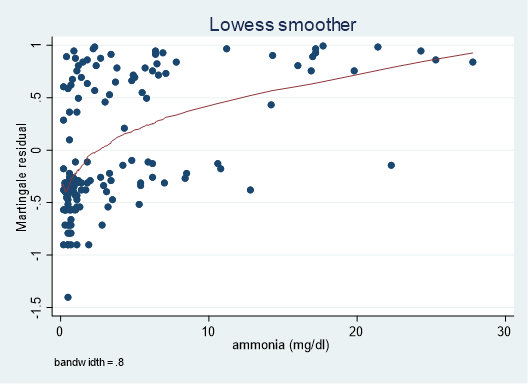
ここで用いたLowess curveですが、これは横軸の各ポイントの平均を滑らかにつないだもの、と簡単に理解しましょう.そしてこのカーブは大きく上にひん曲がってます.試しに対数をとってみましょう.
gen lam = ln(ammonia)
lowess mg lam
ちょっとだけまっすぐになりました.だからこっちのがいいでしょ、とのことです.う~ん、なんだかなぁという感じです. (本当はもうちょいまっすぐになってほしかった…)
approximately linear smooth plot and leads us to believe that the log transformed ammonia variable is better for inclusion in the model.
stcox lam treat, estimate
est store A
stcox ammonia treat, estimate
est store B
est table A B, stats(n aic bic)という具合に比較すると、確かにAのほうがAICもBICも小さいです.Log likelihoodは大きくなります.
2.Goodness of fit
さて、ここからはモデルの適合性についてよく用いられる方法をまとめてみます.
ここでは前述のように、Cox-Snellの残差を用います.
stcox treat lam
predict cs, csnell
stset cs, fail(dead)
sts gen H = na
line H cs cs, sort ytitle("") legend(col(1))このように入れると、45度線に巻き付くような感じでそれほど悪くはなさそうだ、という判断になります.
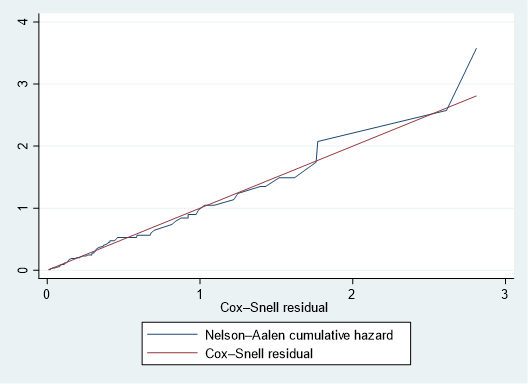
(2025/1/5追記)Stata18の新機能として、この残差プロットの簡略化が行われましたのでご紹介します.
use http://www.stata-press.com/data/cggm3/reyes, clear
stset
gen lam = ln(ammonia)
stcox treat lam
estat gofplot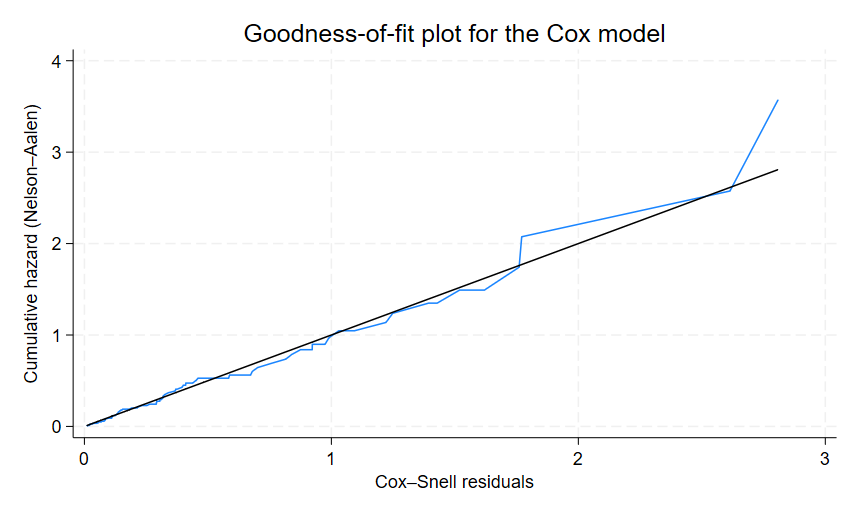
stcoxを走らせた後に、estat gofplotと入れるだけでよいので、簡単になりましたね.
3.外れ値とその影響を調べる
次に、外れ値とその影響力について調べてみましょう.
use http://www.stata-press.com/data/cggm3/reyes, clear
gen lam = ln(ammonia)
qui summarize sgot
replace sgot = sgot - r(mean) /* 平均値を引いて「中心化」 */
stcox treat lam sgot ftliver
predict dfb*, dfbeta /* DFBETA という指標で、影響力を見ることができる */最後、一番のキモのコマンドであるDFBETAを各変数ごとに作成しています.
アスタリスクがついていますが、Coxモデルの変数の順に求められています.
scatter dfb3 _t, yline(0) mlabel(id)
これをすべての変数において実施するというのが1つの方法です.そして、症例ベースで、この症例を抜くとLog likelihoodが大きく変わるかどうか、というのを調べる方法もあります.
Likelihood displacement valueとかLMAXとか呼ばれています.
stcox treat lam sgot ftliver
predict ld, ldisplace
predict lmax, lmax
scatter ld _t, yline(0) mlabel(id)
scatter lmax _t, yline(0) mlabel(id)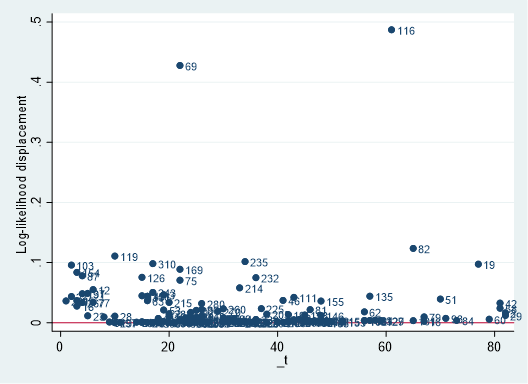

Likelihood displacementでは、ID=69と116が、LMAXではID=116の症例がそれぞれ影響力大きいと判断できます.予測モデルなどを立てるときにはこのように強い影響力を持つ症例を除外するのも1つの方法かもしれません.
まとめ
いかがだったでしょうか?Coxの残差についてまとめてみました.正直ここまでのことを知っている必要があるのか、と言われれば、それほどでもないですね、と答えそうですが、こんなのもあるんだなくらいには知っていてもよいかもしれません.
それにしてもCox比例ハザードモデルの残差は奥が深いですね.ここまで詳しく、そしてわかりやすく書いている本はないと思いますので、この本は買い!ですね.


コメント