このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回は「分割時系列デザイン」という分析手法をStataで実施するための方法についてまとめてみました.ちょっと前にセミナーなどでこのデザインには目をつけていたのですが、そのセミナーではRを使って解説をされておりました.
Stataでやってみたいな~と考えている方も、自分を含めて少なくなかったのではないかと思いましたので、まとめてみることにしました.
1.分割時系列デザインとは
分割時系列デザイン、英語ではinterrupted time–series design, ITSなどと呼ばれております.
何らかの介入が集団に対して行われたとき、その効果がそれまでの状態や推移をinterruptすることから名づけられました.
対照群を設けることなく、何らかの介入の前後の時系列分析結果を比較することで、その介入の効果(影響)を推定することができます.
【強み】
単一の集団を追跡していることで、
- 集団内の年齢の分布や経済状況の分布等を無視できる
- 未知・未測定交絡が無視できる(=RCT)
- 集団レベルでゆっくりと変化する特徴は、時間をモデルに含めることによって制御できる
どんな研究に使えるかというと、例えば次のような例を考えてみましょう.
- 禁煙に関する法令が1989年に実施され、たばこの売り上げが変化してきていることを示したい。
- 売上が1989年前後で変化しているかどうかを客観的に評価するにはどうしたらよいか?
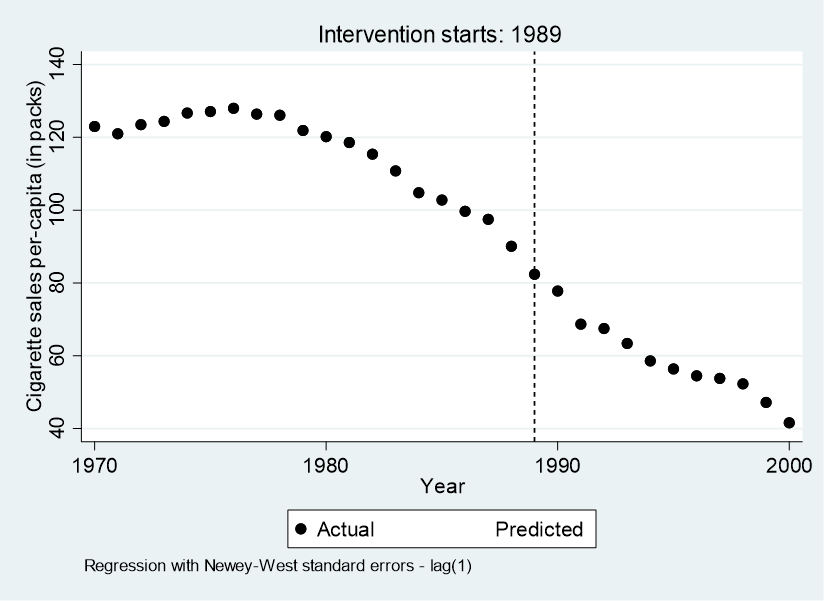
介入の前後のトレンドに違いがあるかを検定する、というのがこの分析の趣旨になります.
ここで使われる統計モデルが、「折れ線回帰モデル」と呼ばれるものです.
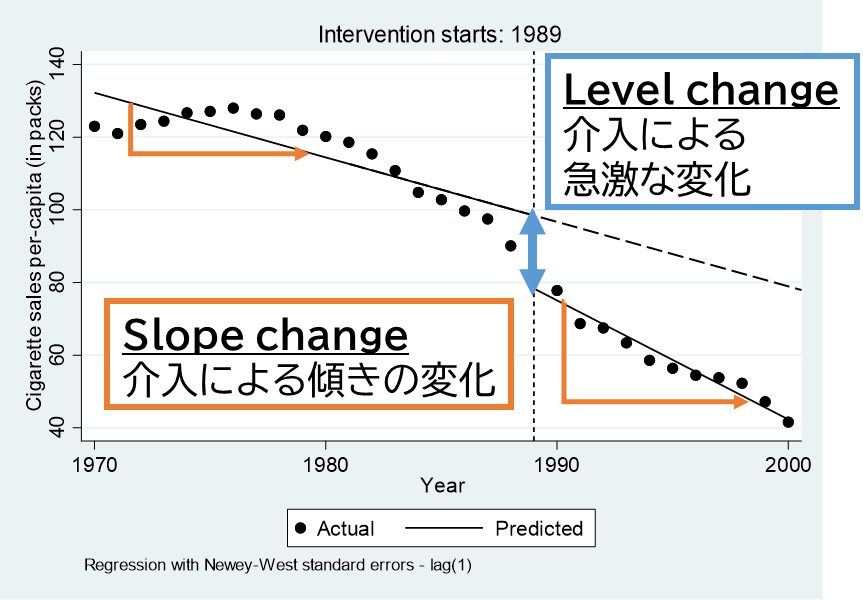
折れ線回帰モデルの式はこうです.
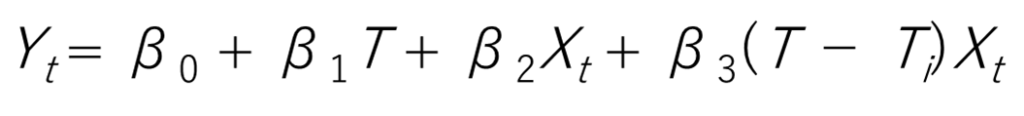
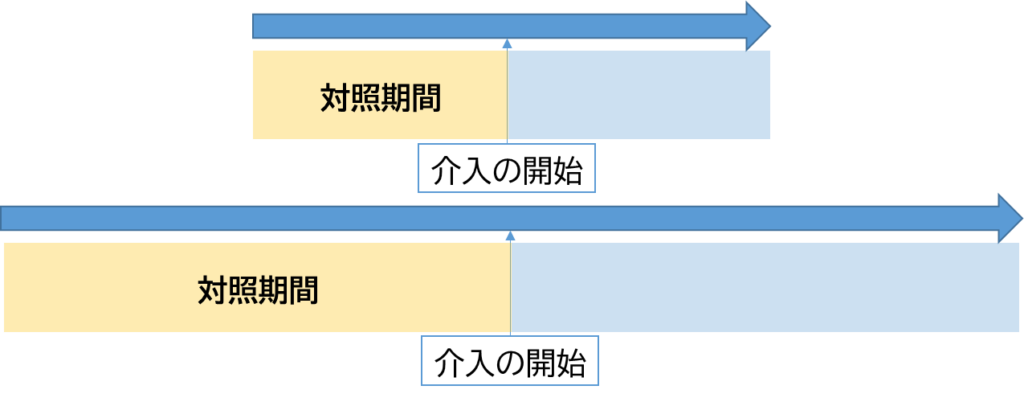
•Xt: 介入の前後を表す指示変数 (0: 介入前、1: 介入後)
•Ti: 介入が始まった時点
データセットはこちらに示すような形で準備することになります.
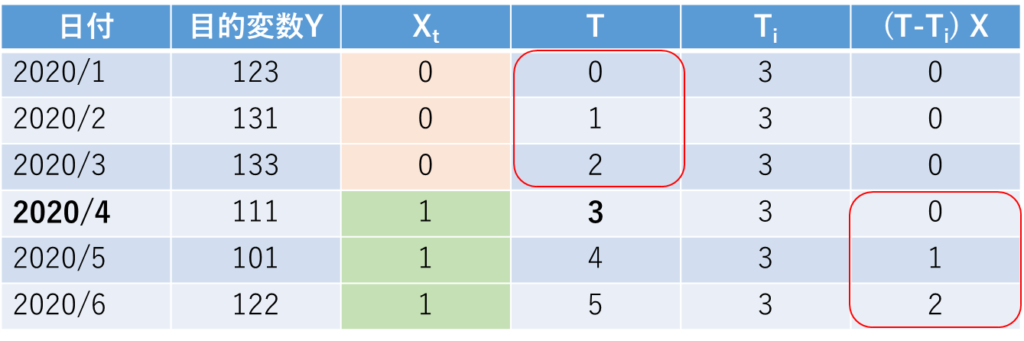
前提としていることとして、前後の時間でその他の要因が(大きく、あるいは不規則に)変化していない、ということが挙げられます.また、何らかの介入が明確なタイミングで行われたような研究によくフィットします.
それと、観察期間が長い方が統計学的な観点からは検出力が上がります.
しかし、その反面、あまりにも観察期間が長いと、その間にいろいろな要因が変化してしまう可能性が高くなります.

また、「自己相関」という問題も検討すべきです.
自己相関?
過去の観測値の影響を受けてしまっていると今回の解析の前提が崩れてしまいます.
自己相関のプロットや仮説検定などを行うことで確認することが推奨されています.(Durbin-Watson test、Breusch-Godfrey testなど)
こういった点に注意しながら研究計画を立てる必要があるわけです.
このデザインで研究を行うためのデータセットとしては、サマリーデータ形式とグループあるいは個人レベルでのデータ形式の両方とも可能です.
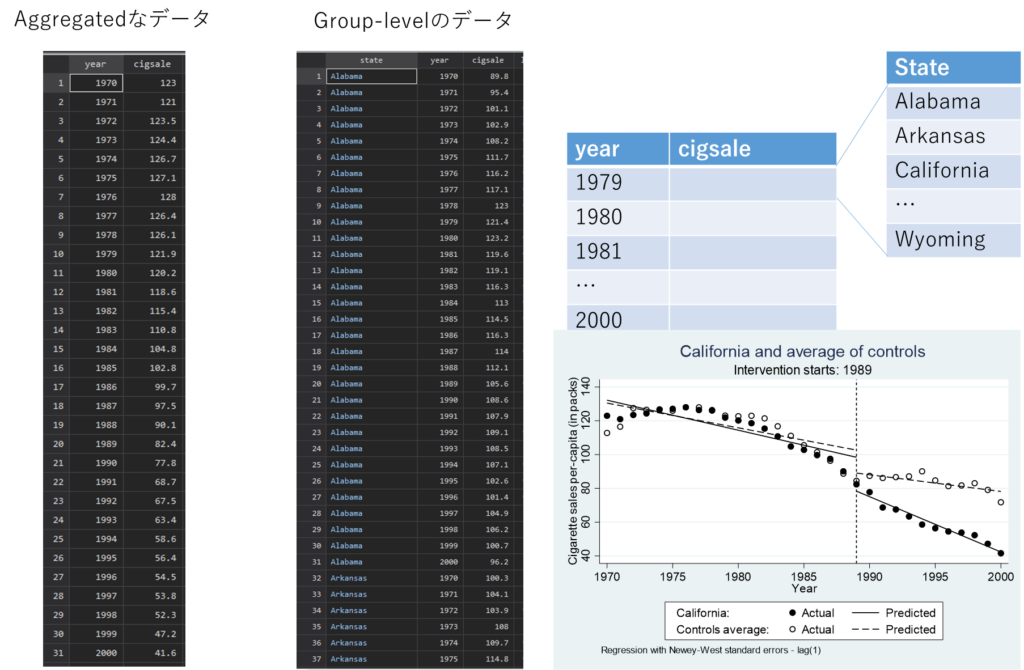
右側のデータのような形式であれば、法令が施行される前後での該当する州と、その法令が施行されない州とで比較することができます.
このような比較対照群を置くことで、着目している介入効果以外の要因の影響を考慮に入れることができます.(Controlled interrupted time series デザインと呼びます)
さらに、個人レベルでのデータをマルチレベル回帰で集団ごとの結果として出力することができます.
下の例は一般化推定方程式で実施したものです.もちろんこの場合もControlled interrupted time series 解析を行うこともできてしまいます.
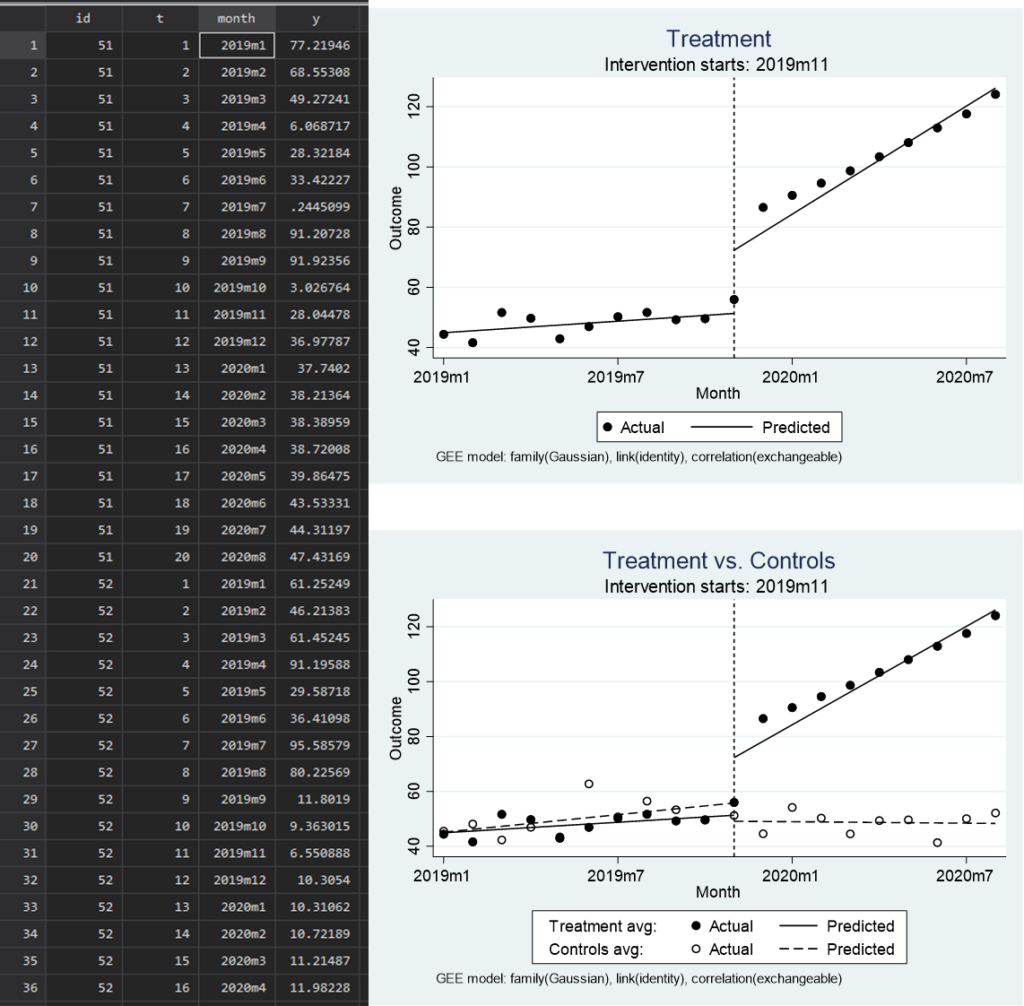
2.Stataで解析を実行するために
さて、ここまででITSについて理解が進んだでしょうから、実際にStataで実施してみたいと思います.
Stataでは、”itsa” というコマンドがUserによって作成されておりますので、それを活用するのが一番手っ取り早いと思います.
マルチレベル解析をしたい場合には”xtitsa” が使えます.
これらのコマンドを使う前に、時系列データの設定やパネルデータの扱いに習熟しておく必要があります.こちらの動画を見ると理解が深まります.
Steffen’ classroom(個人のYoutube)
1.tssetで時系列分析の宣言
“tsset”は、データセットの時系列設定を管理するコマンドです.
.tsset timevar
と宣言することで、メモリ上のデータを時系列にすることができます.
これにより、Stataの時系列演算子を使用したり、tsコマンドでデータを分析したりすることができるようになります.
.tsset panelvar timevar
は、データをパネルデータ(横断的時系列データとも呼ばれ、panelvarの値ごとに1つの時系列を含む)にすると宣言しています.
panelvarというのは例えばIDとかにすれば個人ごとのデータである、と認識されます.
これにより、データをxtsetすることなく、xtコマンドでデータを分析することもできます.
次にオプションについてですが、オプションは大きく二つに大別されており、unitoptionとdeltaoptionがあります.
unitというのは時間幅のことを指します.詳しくは次の項に説明していますが、daily, weekly, monthly, quarterly, yearlyといった時間幅を指定します.
deltaというのは解析対象となる時間の間隔です.
通常はdelta(1)とすると思います.
2.時間幅の選択とそのためのデータ準備
daily, weekly, monthly, quarterly, yearlyとありますが、その幅に必要な変数の作り方をマスターしておく必要があります.
すでに日付データになっている場合には、
- qofd(日付変数)
- mofd(日付変数)
などの関数を使って次のような値が入った新たな変数を作ることができます.
- 2019q4 … 2019年の第4四半期
- 2020m6 … 2020年の6月
こうした値は、表示がこのような数字と文字列の混合になっているように見えますが、数値データとして扱われます.
これらの関数を使って新しく変数(シリアル値)を作成したあとにformatでお望みの形式に表示させることができるようになります.
yearmonthという変数にしてYYYYmMMの形式で表示させたい場合には、
.format yearmonth %tm
とすればよいわけです.
なお、データセットの都合上、日付データが数値データでYYYYMMとなっている場合には、一工夫が要ります.
1.Stringにして、YYYYMM01にする.それをdate関数で日付の連続データとし、上記関数を使う
tostring yearmonth, replace force
gen date1 = yearmonth + "01"
gen date2 = date(date1, "YMD")
gen mdate = mofd(date2)
format mdate %tm2.Numericのままで扱うのであれば、 ym関数を使って新しいシリアル値を作成する
gen mdate = ym(floor(yearmonth/100), mod(yearmonth, 100))
format mdate %tmこのようにすればよいわけです.
3.itsaコマンドを使ってみる
さて、ユーザーコマンドである”itsa” を早速使ってみましょう.その前にダウンロードです.
.findit itsa
と入れていただくと、次のような画面になります.
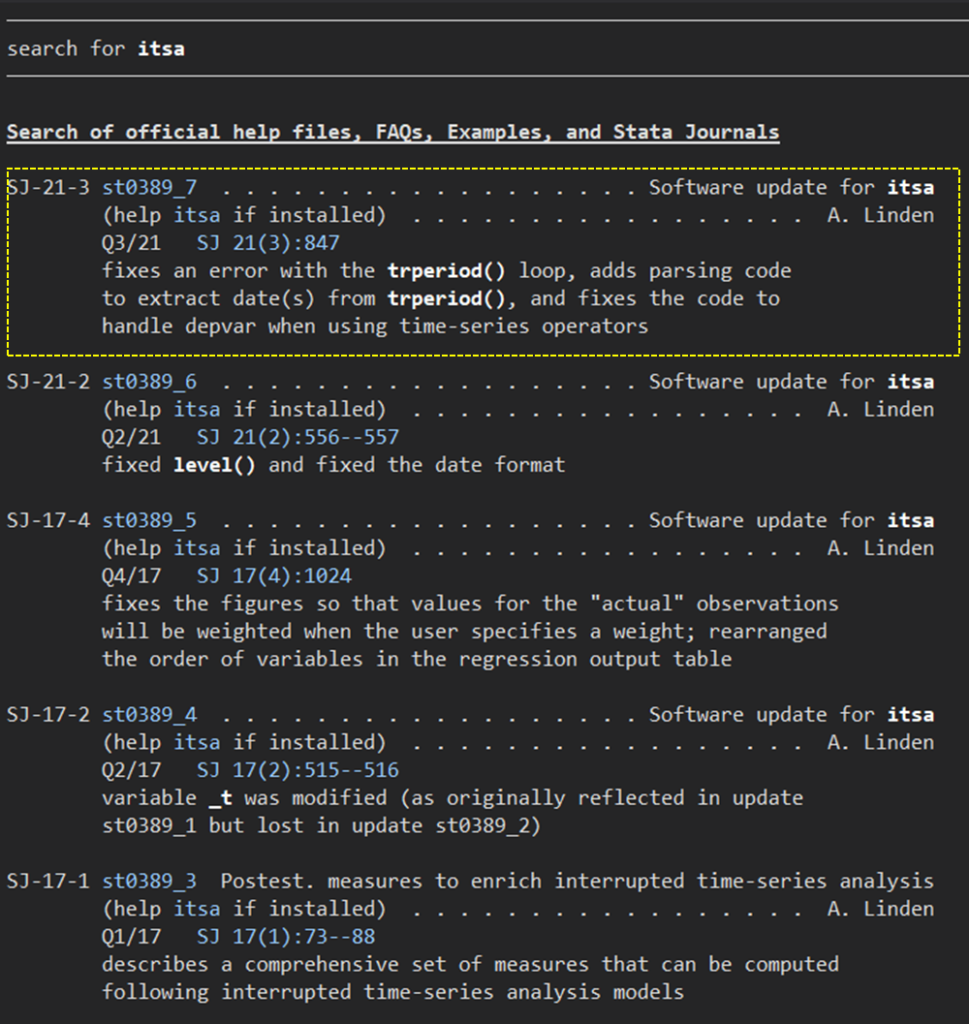
一番上のst0389_7をクリックしていただくと、ダウンロード可能な画面になります.
adofile, hlp(help) fileだけではなく、その下のデータセットも入れておくとサンプルデータを走らせて確認、という作業がワンクリックでできるので、ぜひ入手しておきましょう.
このコマンドを使ったITSの流れは以下の通りです.
- 時系列データセットを準備する
- tsset で時系列データであることの宣言をする
- itsa コマンドを実行する
- 自己相関の確認
先ほどのado fileをインストールする際にゲットしたデータセットを使って確認してみましょう.
use cigsales_single, clear
tsset year /* 時系列データの宣言 */
itsa cigsale, single trperiod(1989) lag(1) figure posttrend
/* たばこの売り上げ(cigsale)を目的変数、
treatmentが1989年に生じた、単群で実行する、図を作成、
1989年後の傾きを算出してください、という内容。
*/
actest, lags(12) /* 自己相関の確認 */
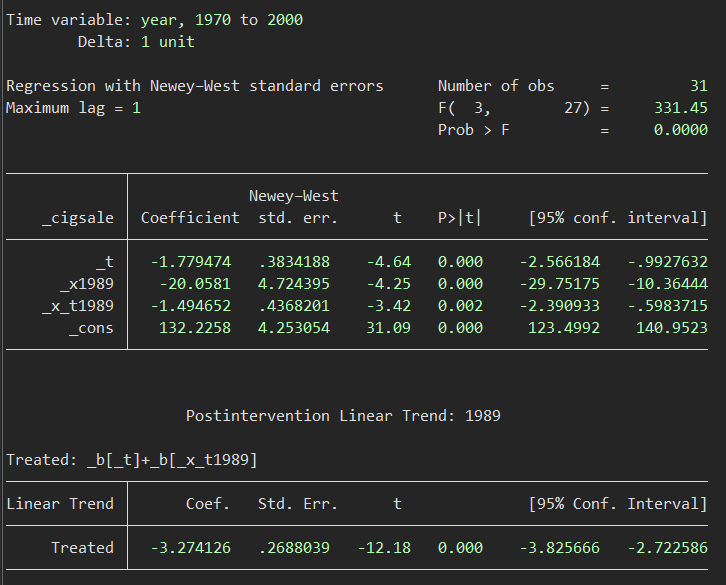
この結果から、1989年以前の傾きは、_tの係数である、⁻1.78 [-2.57 to -0.99]となり、1989年の法令施行という介入によるlevel changeは_x1989の係数である、-20.1 [-29.8 to -10.4]となります.
post intervention trendは-3.27 [-3.83 to -2.72]というのが計算結果として得られていますね.
actestの結果はというと、
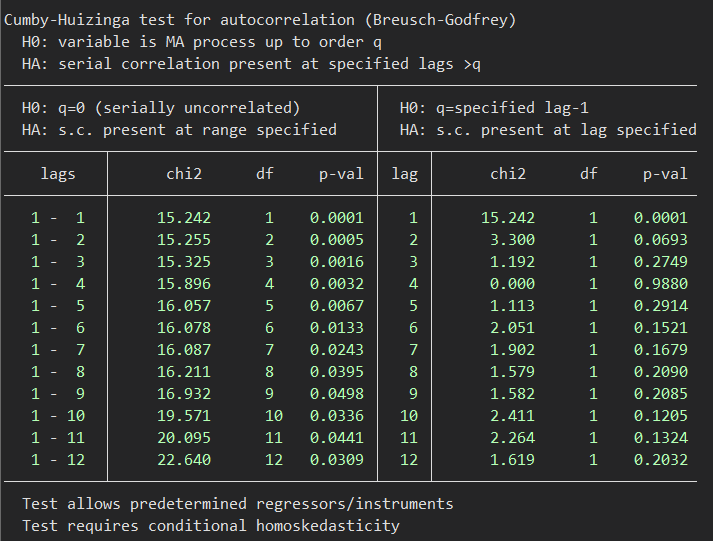
自己相関しまくり、という結果になりそうです….
このactestというのもユーザーが作ったものです.
自己相関の確認もばっちりできるので、論文にも耐えるかなという印象です.自分も早速使ってみたいと思います.



コメント
はじめまして。いつも勉強させてもらっています。
一つお教えください。
actestの結果、自己相関しまくり、ということですが、自己相関している場合はこの分割時系列デザインの結果は信頼できないということになるのでしょうか?どれくらい自己相関については考慮すべきなのでしょうか?