競合リスクとその解析方法をStataでどのようにして実装するのかを理論編と実践編ということで解説していきます.
まず今回は理論編ということで、以下のコンテンツに沿って概説します.
1.競合リスクとは
複数の別の種類のイベントがあり、最初の1つしか観察できないことを競合リスクの問題といい、注目している以外のイベントによる観察の終了が起こることに起因します.
具体的には、悪性腫瘍の再発に注目しているとき、「死亡」が競合イベントとなります. すなわち死亡すると再発できないため、再発が観察されないということです.
通常の生存時間分析においてはこういったイベントは「打ち切り(Censoring)」として扱われますが、競合リスクを考慮にいれた解析では「打ち切り」として扱う場合とそうでない場合とに大別されます.
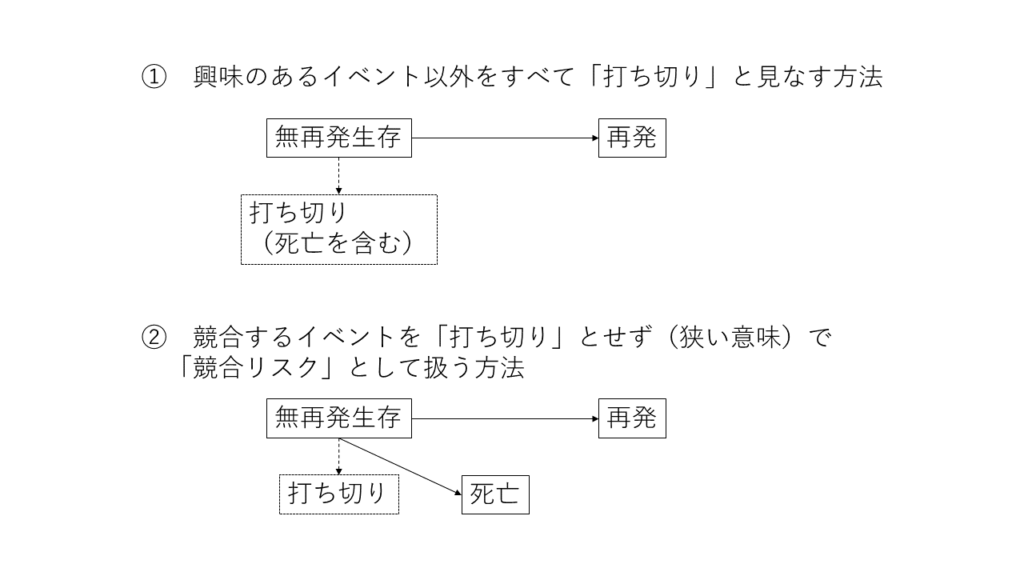
このように興味のあるイベント以外のイベントをどのように扱うかによって、書くイベントの発生確率の合計が変わります.
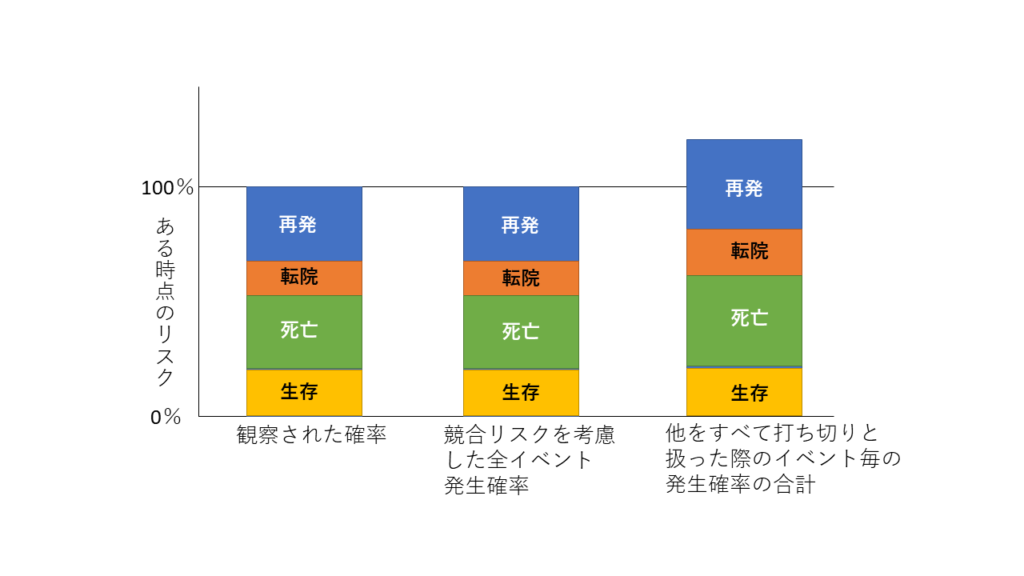
興味のあるイベントを再発としたとき、死亡を競合リスクと見なした場合である②は上の図でいうところの真ん中になり、打ち切りと見なした場合である①のは一番右になります.
このように、 競合リスクの存在下において、ある事象の発生確率を推定する場合には競合リスク分析を行わなければ誤った推論になる可能性が高い、ということになります.
2.競合リスクデータの解析の目的
これまでの話からすると、競合リスクの問題が考えられるなら片っ端から競合リスク分析をすればいいじゃないか、と思われるかもしれませんが、実際にはそうでない論文もたくさんあります.
いずれにしても、興味のあるイベント以外のイベントが、競合リスクであるかどうか、というのは常に考えておく必要はありそうです.
その上で、競合リスクの考えを導入するには以下のような目的が考えられます.
- イベントごとに独立変数の影響を検討したい(原因別にハザード比を検討)
- イベントごとの発生確率を推定したり、予測モデルを構築したりしたい
簡単に言うと、後者の場合には競合リスク解析の考え方、すなわち冒頭の②を使い、前者は原因別ハザードを推定する方法であればよく、①を使う、ということで覚えておいて問題ないようです.
ただ、これについては他にも意見がありますので、それも含めて文献情報を紹介しておきます.
- Lau,et al. (Am J Epidemiol 2009; ;170(2):244-56)目的に応じた使い分けをすべき
- Cause-specific PHはリスク因子や原因の分析に向く⇒①
- Fine-Grayは群間のイベント発現確率の分析に向く⇒②
- Latouche,et al. (J Clin Epidemiol2013; 66(6):648-53)すべてのイベントごとにcause-specificPH modelsによる解析結果とCIFを示すことを推奨
- Li, et al. ( J Am Soc Neph 2019; 30: 2284-2286) “the cause-specific hazard model is often more suitable for studying etiology,i.e., the association between covariates and the instantaneous risk of a clinical event,whereas the subdistribution hazard model is more suitable for prediction,i.e., estimating the future probability of the event.”
- “普通のCox回帰は因果推論にはよく、競合リスクモデルは予測モデルを作るのに適している”
- 留学先のPennsylvania大学の疫学・生物統計学部門で一緒に研究していた生物統計家が2nd authorに名を連ねていました.
3.カプランマイヤー法とCumulative incidence法 -生存曲線の推定-
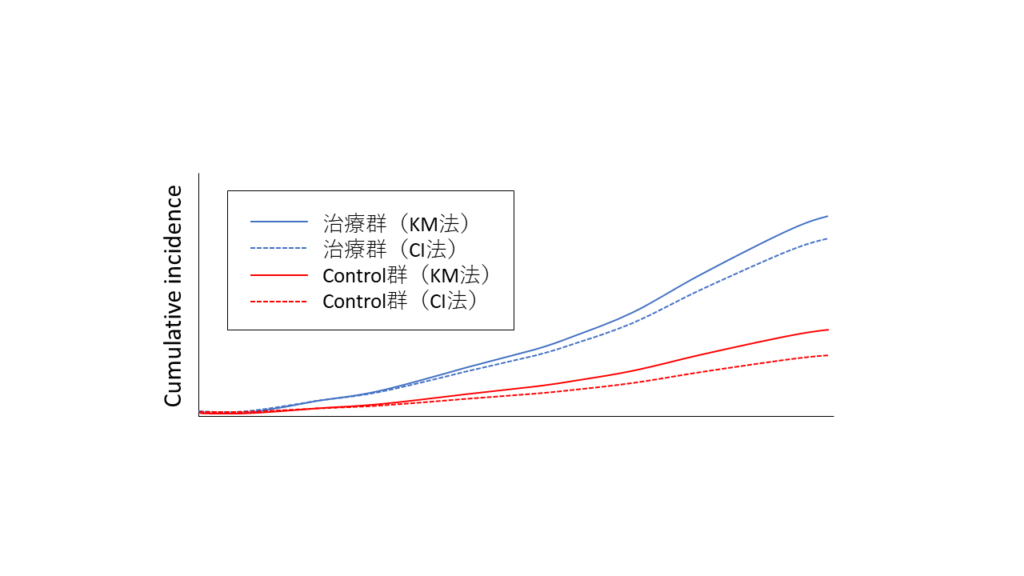
競合リスクイベントを打ち切りとするかしないかによって、生存曲線は変わってきます.
カプランマイヤー法では、event-free survivalを縦軸にして右肩下がりのグラフになるのですが、イベント発生に着目すると、”1-KM”とも言われますが、右上に伸びていくグラフになり、縦軸はcumulative incidenceになります.
ただ、このとき、主要なイベント以外はすべて「打ち切り」として扱われますので、at-risk集団から除かれる(次のイベントの影響力が大きくなる)ことになります.
競合リスクとして扱う場合、これをCumulative incidence法と呼びますが、このとき、打ち切りにならないため、at-risk集団に留まります. そのため、次のイベントの影響力が相対的に小さくなります.
まとめますと、以下のようになります.
- 大小関係は、カプランマイヤー法によるイベント確率>=Cumulative incidence法によるイベント確率
- 各イベントの発生確率を足し算すると、Cumulative incidence法では合わせて100%になるのに対し、カプランマイヤー法では100%を越える場合がある.
- カプランマイヤー法の場合は競合リスクのハザードに依存しない. 死亡を競合リスクとした再発事象を検討する研究においては、死亡のハザードが再発確率に影響しないのがカプランマイヤー法で、再発・死亡の両方のハザードによって決まるのがCumulative incidence法である.
4.競合リスク解析におけるモデル
競合リスクイベントを打ちきりとして扱う場合には、原因別ハザードモデルを競合リスクとして扱う場合にはFine & Gray モデル、と単純に覚えましょう.
ちなみに前者は形の上では通常のCox比例ハザードモデルと全く同じ方法で計算します.
ここで、これまでの流れをまとめると、次の表のようになります.

文献を適当に調べてみて、どんな場面で競合リスク解析を用いられているかを列挙してみました.
| 対象集団 | 主要イベント | 競合リスク | 文献 |
| 腹膜透析患者 | 腹膜炎 | 血液透析への移行/腎移植 死亡 | 1 |
| HIV患者 | 癌 | 死亡 | 2 |
| Stage 4 CKD患者 | 末期腎不全 | 死亡 | 3 |
| 米国人 | 原発性肝がん発症および死亡 | 他の原因による死亡 | 4 |
- Teixeira et al. BMI Nephrol. 2013; 14: 110.
- Yanik et al. AIDS. 2016; 30: 1663-8
- Ravani et al. J Am Soc Nephrol. 2019; 30: 2219-2227
- Zhong et al. Int J Cancer. 2020 [Epub ahead of print]
5.まとめ
ひとまずここでは、因果推論にはCause-specific hazard modelを使い、発症確率や予測モデルにはFine & Gray modelを使う、と単純に覚えておくことにします.
ちなみに、比例ハザード性は常に気にしろよ、とかつての同僚の生物統計家が述べていましたので、そこが重要なのでしょう.さらに詳しく学びたい方は、コチラへ.次回はいよいよ実践編です.Stataで実際にCumulative incidence法でグラフを描いてみることにします.


コメント
[…] 前回、前々回の記事では競合リスク解析の理論と実践の初歩について説明しました.今回はちょっとした応用編です. […]