Multiple imputationについて②実践編

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています． ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて今回の記事では、多重補完について、Stataでの実装の仕方について解説したいと思います．理論編はコチラからどうぞ．また、多変量解析の検定結果を取り出してマクロにしたり、P値を取り出したりする方法についてはコチラからどうぞ．

1．多重補完の宣言

Stataで多重補完をするときは生存時間分析のときのstsetのように、

「多重補完を今からやりますよ」

という宣言を行います．そのとき、どんな形でデータセットを表示するかを選ぶことが必要です．Stataでは次の4つのStyleから選択することになっています．

1. wide: 欠損のあるデータに対して補完したデータを入れたものを横に横につなげていく
2. flong: 欠損のないデータを含むすべてのレコードを縦につなげる
3. mlong: 欠損のないデータはm=0のみ、欠損のあるデータのみすべてのデータセットに
4. flongset: flongを別々のデータセットに格納する

その前に欠損値がどの程度あるのか、欠損のパターンがどうなっているのかについてあらかじめ見ておくことをお勧めします．その際に便利なコマンドが、

misstable summarize varlist
misstable pattern varlist

これで欠損値がどのくらいあるのか、そしてどんなパターンで欠損しているのか、についての大まかな情報をつかむことができます．

それが終わったら多重補完の宣言をします．

wide型

webuse miproto
list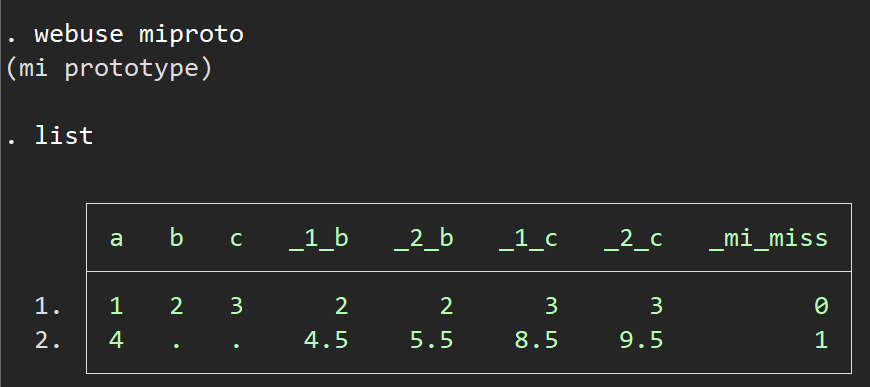

欠損したデータが横に横に連なるようなイメージがつかめるでしょうか？

2．flong型

上の例と同じようにb、cに欠損値が存在しているときに、以下のようにデータセットが作られる想定になります．

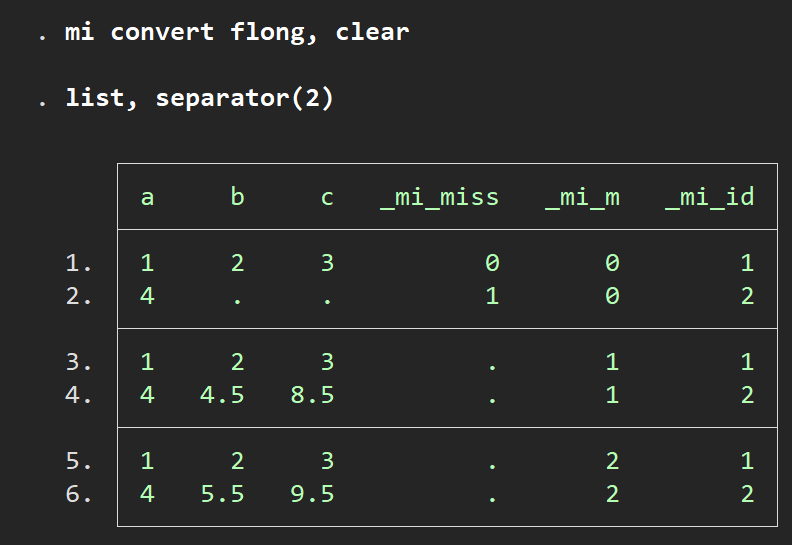
m＝0のデータセットは欠損値を含むオリジナルのもので、欠損値を埋めたデータセットはm=1, m=2になります．欠損のないデータも含めて複数のデータセットを縦に連ねる場合、flong (full longってことか？)と指定してやります．

mi convert flong, clear
list, separator(2)

ここでmi convertとしたのは先ほどのデータセットがwide型だったのをflong型に変えたい場合にはこのようにすればよいです．

3．mlong型

上のflong型では欠損値のないデータも重複して表示されていましたが、その重複はうざいですよね．記憶容量を食ってファイルが重くなるだけです．そこでそのような重複を避けるためにこの型をよく使います．

mi convert flong, clear
list, separator(2)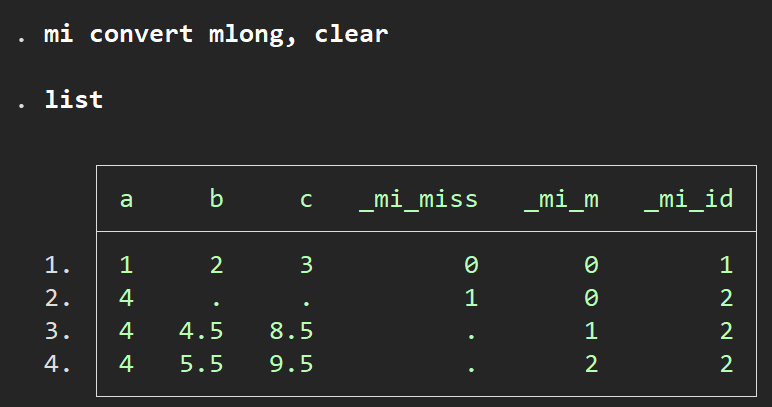

先ほどの表と見比べていただければその違いがはっきりするでしょうか．

欠損値のない1行目のレコードが再び出てこずに代入後のデータだけが淡々と出現するという構造です．

4．flongsep型

これはflong型と同じく欠損のないレコードが再び出現するものですが、違うのは別のデータセットとして格納してくれるという点です．（個人的にはあまりつかわないかな）

2．変数を登録する

続いて”mi register”で変数を登録します．ここには3つの登録の仕方があります．

mi register imputed varlist
mi register passive varlist
mi register regular varlist

imputedとするものは欠損を補完する変数群です．regularは欠損の有無にかかわらず補完を行わない変数です．passiveは欠損があってimputeされる変数からの変形で埋まるものを指します．

このとき、連続変数の分布が正規分布でない場合（right skewなとき特に）対数変換が勧められます．注意したいのは、対数変換するときに底が0であっては変換ができないという点です．

例えば収入はゼロの値をとりえて非正規分布な変数の代表格です．次のような仕掛けをしておくことが肝心です．

generate lnincome = log(income)
replace lnincome = .a if lnincome==. & income!=.
  /* 欠損値でも意味をそれぞれにつけることができる */
*** passiveで登録．欠損値.aに再度0を代入する、としておく
mi register passive income
mi passive: replace income = cond(lnincome==.a, 0, exp(lnincome))

3．補完プログラムの設定－chained equation－

いよいよここでimputationを実施するための関数を設定します．ここではchained equationで行うことにします．help画面を検索すると、いろいろな関数が使えることがわかります．

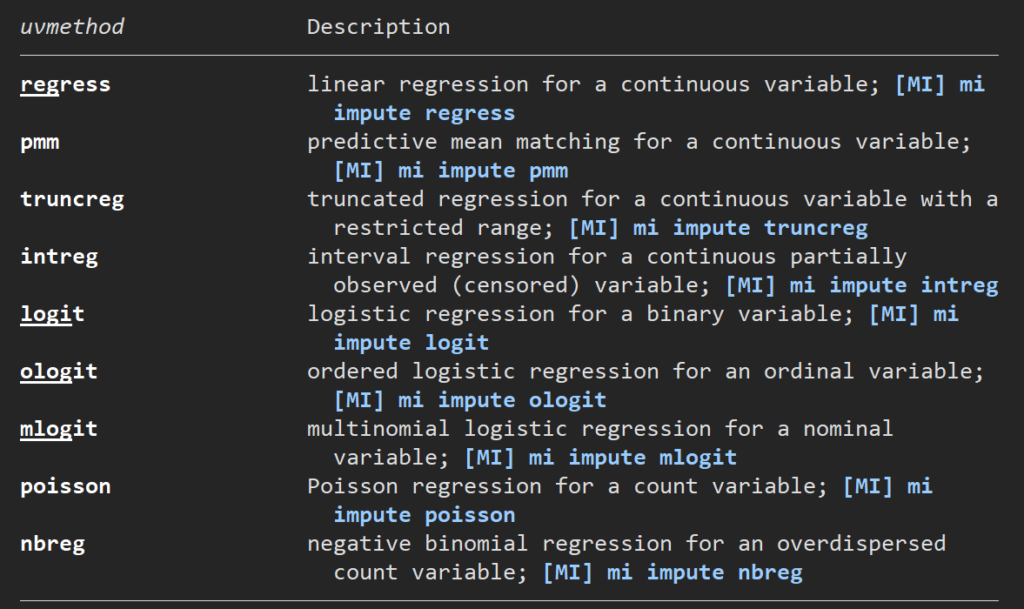
#delimit ;
	mi impute chained 
		(regress) varlist1
		(logit)  varlist2
		(mlogit)  varlist3
		= varlist4
	, add(20) rseed(2210)
	;
#delimit cr

線形回帰をあてはめて値を補完するものをvarlist1, ロジスティック回帰をあてはめるものをvarlist2, 多項ロジスティック回帰をあてはめるものをvarlist3で挙げて、regularで列挙した変数をvarlist4に並べます．

何セットのデータセットを重ねるかをadd()で指定します．よくやられるのが20セットなのでここでは20としています．

また、結果を毎回再現するためにseedを設定します．rseed()のところに適当な数字をいれましょう．

これでデータセットは多重補完法によって補完されました．このあと集計をしたり推定を行ったりするわけですが、新たに変数を作ったりする場合には、“mi xeq:”のあとにgenerateやreplace, etileなどのコマンドを置くようにします．

また、回帰モデルを作る場合には”mi estimate:“のあとに通常のコマンドを入力しましょう．

生存時間分析の宣言は”mi stset“としてください．あとから係数を取り出したい場合には、“mi estimate, post: “としてから入力を続けるようにしてください．

まとめ

今回は多重補完法の実際の書き方について解説しました．理論を学んだうえでぜひチャレンジしてみましょう．こちらを参考にどうぞ！

また、日本語で勉強されたい方はこちらもお勧めです．