P値を計算する方法 ③ 多重補完後の結果を取り出す | 医療統計とStataプログラミングの部屋

回帰モデルを実施した後に、P値や推定値を取り出すのに、

_b[var], _se[var]

などのようにすることでその値を取り出してプログラムに組み込むことができました.

Multiple imputation (MI, 多重補完法)を実施したあとの結果を取り出すときは少しだけ工夫が必要です.

主な違いは２つあります.

結果がcoefficientとvariance (standard errorではない)
結果がmatrixとして格納されており、取り出す方法が異なる

これを踏まえて変数を取り出す手順を説明します.

1．MI後のデータから値を取り出す準備
2．マトリックスの構造について
3．必要な数値を取り出す
- 1）coefficientを取り出す
- 2）SEを取り出す
4．プログラム例
5．まとめ

1．MI後のデータから値を取り出す準備

Stata Pressが出しているデータセットを使うことにします．”attack”という目的変数に対してsmokes, age, bmi, hsgrad, femaleという説明変数を投入するロジスティック回帰分析をMI後のデータセットで実行します．

このとき、mi estimate: command というのがセオリーなのですが、以下のように、post というオプションを入れることが最初の一歩になります．これがないと全く始まりません．

use http://www.stata-press.com/data/r13/mheart1s20
mi estimate, post: logit attack smokes age bmi hsgrad female

これで第一段階の準備は整いました．次に、変数をマトリックスから拾ってくる、というところを説明します．これがなかなか理解できなかったんですよね…。

2．マトリックスの構造について

格納されている推定値や分散がマトリックス（表）の形で保持されているということを知っておく必要があります．以下のようにコマンドを打つと、coefficientだけリスト化できます．ここで、coefficientはexponentiateされていないのでlog(odds ratio)になります．

matrix list e(b)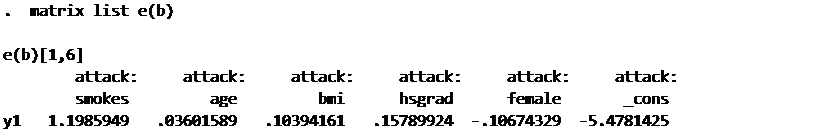

こんな結果がでてきます．これがさっきのロジスティック回帰の出力結果のcoefficientに合致しますね．次に信頼区間やP値を計算するためにstandard errorを出したいのですが、分散共分散行列がe(V)に格納されているので、少し細工が必要になります．

さらに、これがマトリックスの形になっているのも注意です．

matrix list e(V)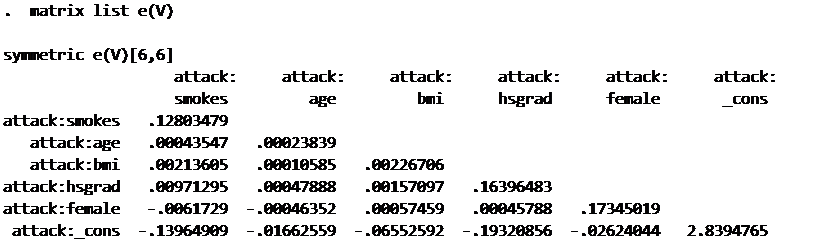

ほしいのはこの中の行数と列数の一致したところだけです．

これらを一旦マクロの形で格納して、必要なものだけ出すようにします.

matrix myb = e(b)
matrix myv = e(V)

マトリックスの形で入れた場合、狙った変数を順番で取り出していきます.

3．必要な数値を取り出す

1）coefficientを取り出す

説明変数をsmokes age bmi hsgrad femaleの順に入れていますので、

smokesのβ値は, myb[1,1]、ageのβ値は, myb[1,2], …

ということで[1,a]とあるうちの2番目の数値であるaを変数の順番に対応させてかえていきます.

2）SEを取り出す

信頼区間やP値を計算するとき必要なStandard errorがなく、代わりにvarianceですので、平方根をとります.

ということで、a番目の変数のP値は以下の式で与えられます.

2*normprob(-abs(myb[1,a]/sqrt(myv[a,a])))

ここで注意なのが、varianceは斜めに結果が格納されているので、[a,a]となります.

信頼区間は

下限がmyb[1,a] – invnormal(0.975)*sqrt(myv[a,a])で、

上限がmyb[1,a] + invnormal(0.975)*sqrt(myv[a,a])で、

となります.

こうして得られたβ値も信頼区間も最後は指数変換しなければORになりません.

4．プログラム例

最後にプログラム例を載せておきます.

use http://www.stata-press.com/data/r13/mheart1s20
mi estimate, post: logit attack smokes age bmi hsgrad female
  matrix myb = e(b)
  matrix myv = e(V)
 forvalues n = 1/5      {   
        local b_`n' = myb[1,`n']
        local lb_`n' = myb[1,`n'] - invnormal(0.975)*sqrt(myv[`n',`n'])
        local ub_`n' = myb[1,`n'] + invnormal(0.975)*sqrt(myv[`n',`n'])
        local p_`n' =  2*normprob(-abs(myb[1,`n']/sqrt(myv[`n',`n'])))
       nois disp  "`n'", %3.2f exp(`b_`n''), %3.2f exp(`lb_`n''), %3.2f exp(`ub_`n''), %4.3f `p_`n''
        }