「傾向検定」とは、標本集団で観察された平均値や割合が、だんだん大きくなる、もしくはだんだん小さくなるというトレンド(傾向)が、母集団でもそうなっているかどうかを検定するものです.
連続変数における平均値やカテゴリー変数の割合(ここでは二値変数になりますが)のほかに、生存分析でおなじみのLog-rank testも登場します.
では具体的にどんな検定が出てくるのでしょうか.そしてStataでどのように実装するかみていきましょう. アウトカムの種類に応じて整理するとわかりやすいです.
1.二値変数の割合:Cochran-Armitage trend test
結果変数が二値、説明変数が順序または数値変数の傾向検定をCochran-Armitage傾向検定と言います . p=a+bxという直線の傾きbが有意かどうかを検定します.
例えば、担任の先生の経験年数と志望校合格割合の間に傾向があるのではないか、ということを証明したい場合を想像してみましょう. (2022/7/26修正)
1組の先生は新人(経験年数0年)で、生徒数100名中合格者10名
2組の先生は5年目で、生徒数100名中合格者30名
3組の先生は20年目で、生徒数100名中合格者60名
4組の先生は30年目で、生徒数100名中合格者70名
のような状況を思い浮かべてください.
コマンドとしては “ptrend” を使います.
ptrend rvar nrvar xvar
/// あるいは以下のようにやることもできます
ptrendi r1 nr1 x1 \ r2 nr2 x2 \ r3 nr3 x3 [ \ r4 nr4 x4 ... ]
/// "i"はimmediate、すなわちデータセットを展開しなくてもすぐできるコマンド上の例で考えると、
ptrend rvar nrvar xvar
ptrendi 10 90 1 \ 30 70 2 \ 60 40 3 \ 70 30 4
/// あるいは以下のようにやることもできます
input teacher_id experience rate failure
1 0 10 90
2 5 30 70
3 20 60 40
4 30 70 30
end
ptrend rate failure teacher_id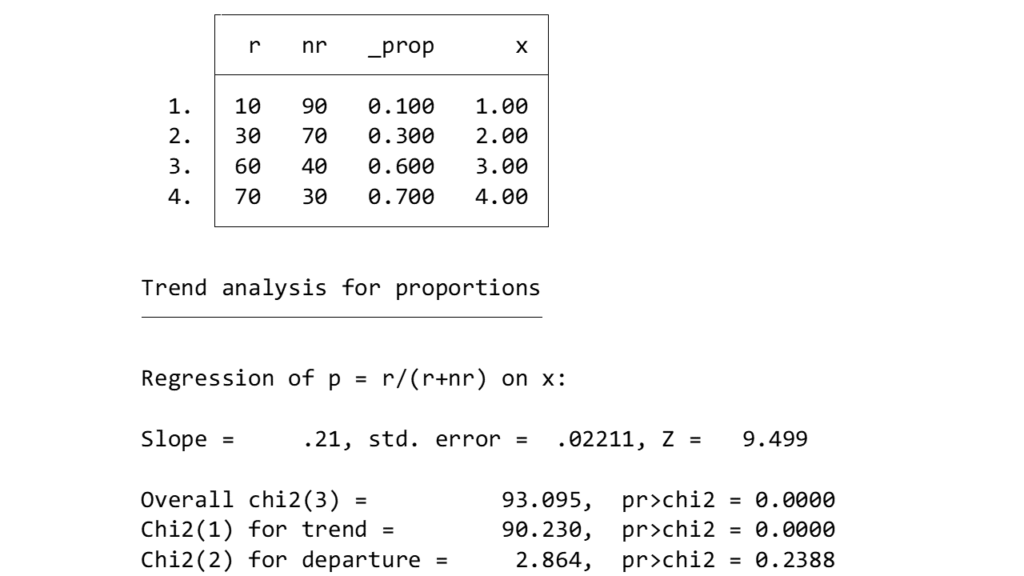
Cochran-Armitage trend testの結果はこのChi2(1) for trendの部分(Qtrend)の結果を見ればよいようです.
ただし、Stata社のQ&Aセッションでは以下のような記載がありました。
Qdeparture (=”Chi2(1) for departure” as Royston’s output nicely labels it) is the statistic for the Cochran–Armitage test. But Qtrend and Qdeparture are usually performed at the same time, so lumping them together under the name “Cochran–Armitage” is sometimes loosely done.
The null hypothesis for the Cochran–Armitage test is that the trend is linear, and the test is for “departures” from linearity; i.e., it’s simply a goodness-of-fit test for the linear model.
Chi2(1) for departure(Q departure)がCochran-Armitage testの統計量であり、この検定の帰無仮説はトレンドが線形であることを意味するので、(線形でない場合にP<0.05となるから)Goodness-of-fit testみたいなものだ、と書いています.
しかしQtrendの部分を報告すればよいということを確認しました.実際多くの論文ではTrendが有意にあるときにはP<0.05と報告していますよね.
Overallの結果は検出力が落ちますが、そもそも傾向検定は、特定の方向性をもった結果かどうかについて検討するものです.
(2022/7/26追記)以前の記事中では、合格割合~%という記載になっていたかと思います.
これは正しくは、全体の人数中の合格者実数と非合格者実数を入力する必要があります.
同じ割合であってもサンプル数によってP値が変化するためです.
100人中10人なのか、10人中1人なのか、割合としては同じですが、統計学的な差の検出力という点では前者に軍配が上がりますので注意をしましょう.
(2021/7/16追記)ここで、Stata 17にUpgradeされてからnptrendコマンドの仕様が変わりました.結論から言えば使いやすくなりました.(Stata新機能 トレンドに対するノンパラメトリック検定)
新しい仕様でのnptrend、まずはhelpを見てみましょう.
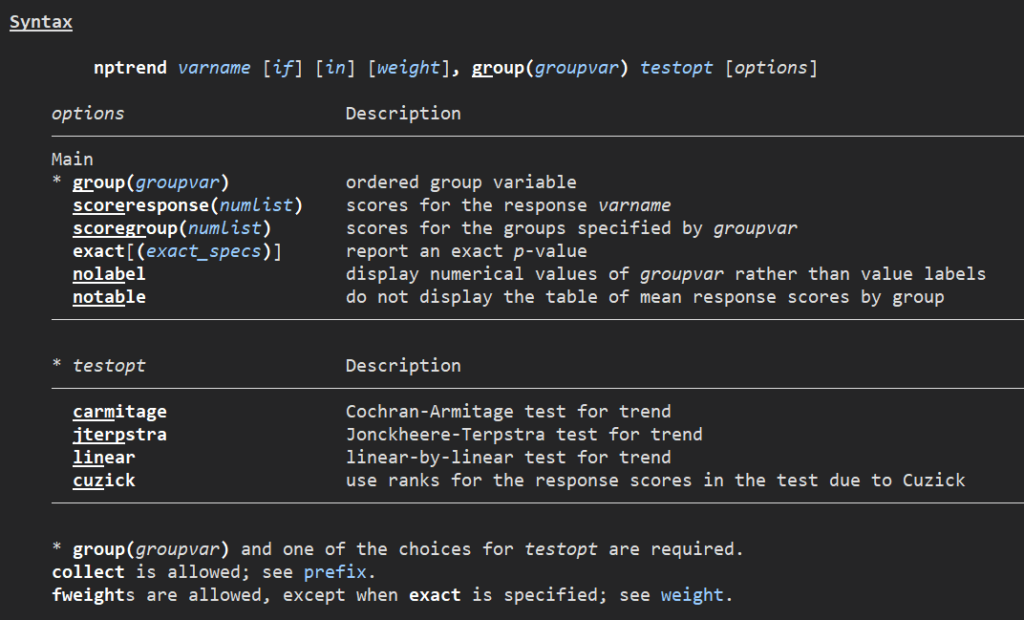
主要な変更点は、これではなく、byをgroupにすることと、test optionを選択しなければならない、という点になります.
test optionは、
- Cochran-Armitage test
- Jonckheere-Terpstra test
- linear-by-linear test
- Cuzick test (これがもともとのデフォルト設定でした)
つまり、Cochran-Armitage testもnptrendでできてしまうようになりました.これのよいところはデータの前処理が圧倒的に楽になったということです.ptrendではresponse rateとnegative response rateを両方データとして準備しなければならなかったため、面倒でした.
nptrendではその必要はなく、
webuse migraine, clear
nptrend relief, group(dose) carmitageこのように入れていただくと結果が出ます.

結果の解釈としては、help画面からリンクをたどって得られたPDFには以下のような記載があります.
The asymptotic p-value for the test of a linear trend is 0.0526. The p-value for the test of departure from linearity is 0.0656.
前述の通り、報告すべきP値は0.0526であって、Goodness-of-fit test的にその下の0.0656は利用すればよいのでしょう.さらにexactオプションを使えば正確検定も実施可能です.
そしてまたさらに、Monte Carlo法を用いた並べ替え検定(permutation test)も実行することができると書いてあります.(詳しい方はどんな場面で使うべきかなど補足説明していただけると助かります.)
webuse migraine, clear
nptrend relief, group(dose) carmitage exact(montecarlo, reps(100000) rseed(1234))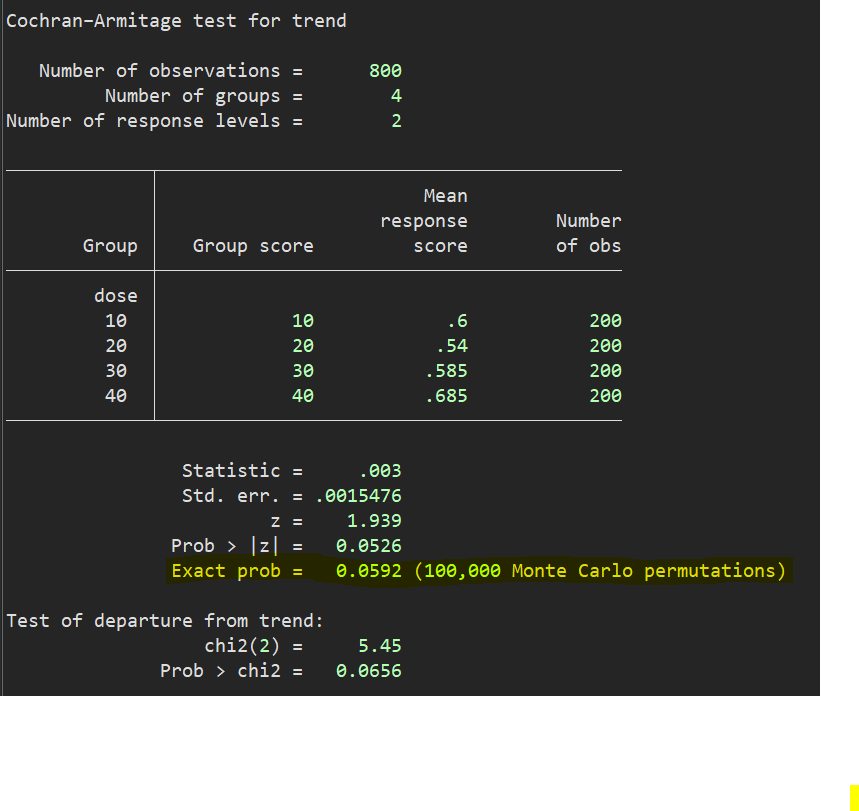
これも正確検定の一種なのですが、得られたP値は0.0592でした.
2.連続変数の平均:Jonckheere–Terpstra trend test
これは二値変数の割合がCochran-Armitage trend testで検定できたのに対し、
ある連続的な値に対する平均値のトレンドをみる、というのが目的になります.
コマンドとしては”nptrend”を用います.helpにある例を使って説明します.
(2021/7/16追記)新しくなったnptrendのコマンドでは下記コマンドは無効となります.
webuse sg
nptrend exposure, by(group)ということでご紹介しておりましたが、下記のようになります.
webuse sg
nptrend exposure, group(group) cuz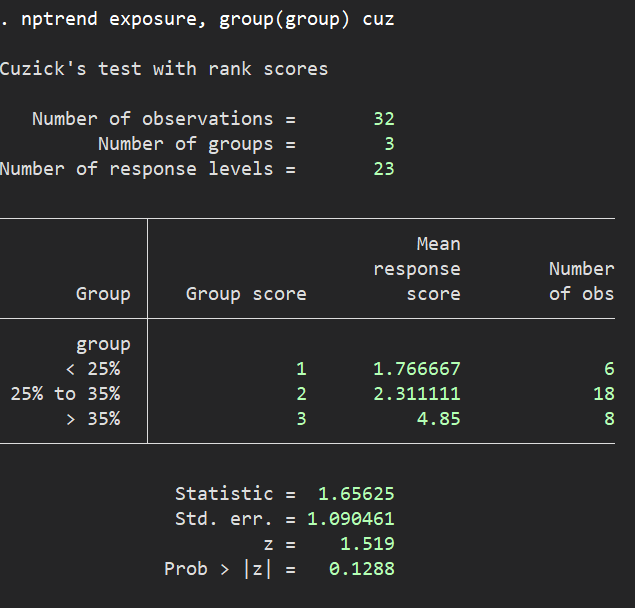
結果はP = 0.129ということで有意な関連はありません、ということになります.
Jonckheere-Terpstra testを行うと少しだけ結果がかわります.

(2021/5/6 追記)ある親切な方にご指摘いただきましたが、Stataのnptrendは実はJonckheere–Terpstra trend testではなく、よく似た別物である”Cuzick test ”を行っているとのことでした.
StataではJonckheere-Terpstra test関して、ユーザー作成コマンドがあります
“jonter” という名前のコマンドです.
“.web install jonter” と入れてみてください.
web install jonter
webuse sg, clear
jonter exposure, by(group)
とりあえず両側検定のものを先ほどのnptrendと比較してみると、それほど値がずれていないようなので、まあ似たようなことをしているのでしょうね.
さてここで、連続値と連続値ではどうしたらよいのか?という疑問を抱く方がいると思いますが、
その場合は散布図+相関あるいは回帰直線(曲線)を作って検定するなどの方法が一般的には取られうる方法と思います.
しかし例えば連続値をある閾値に従ってグループ化→順序変数に置き換える、
といった手続きを踏めば上記の方法を使った検討は行うことができます.
またいつものautoのデータを使います.車体が重くなるほど値段が上がる、というトレンドを見ていきます.
散布図ではそんな感じに見えます.
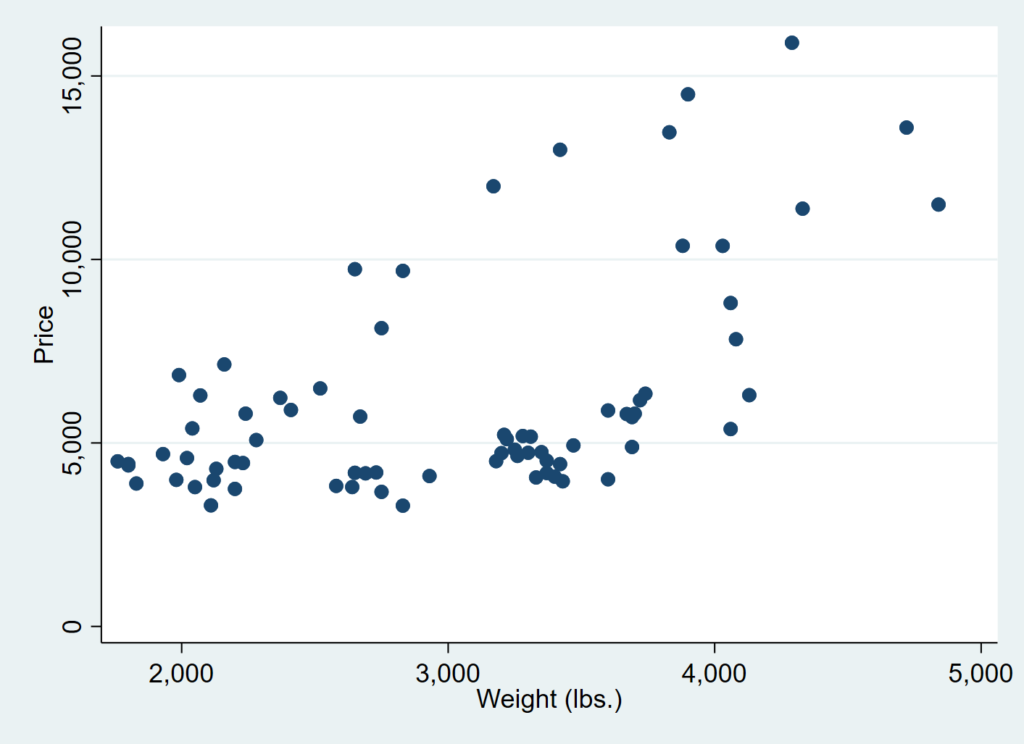
sysuse auto, clear
recode weight (min/3000 = 1) (3000/4000 = 2) (4000/max = 3), gen(weight_cat)
nptrend price, group(weight_cat)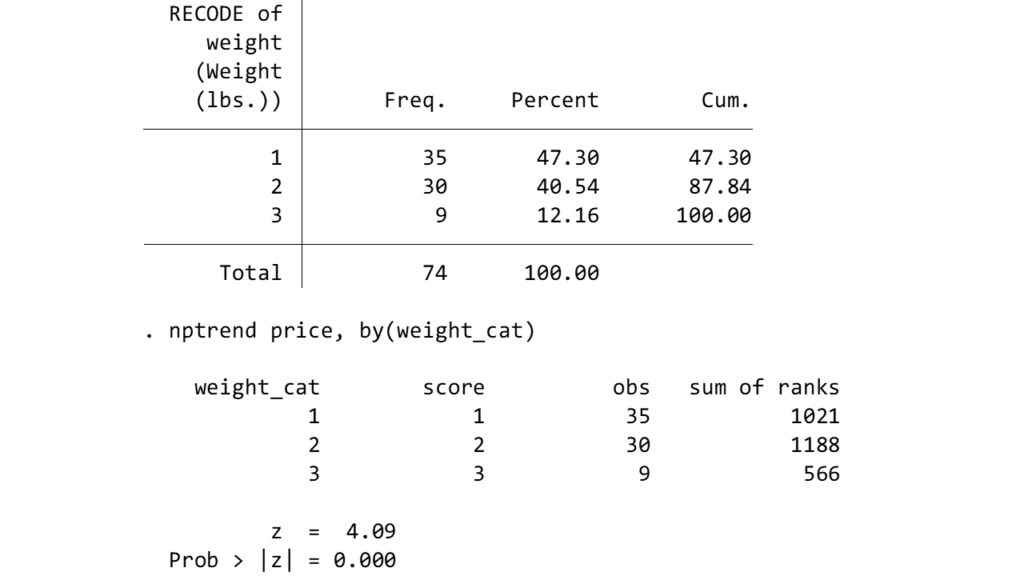
3.生存時間分析:Log-rank trend test
最後は簡単です.Log-rank検定で、例えば曝露因子が連続値の4分位点によってグループ化してある変数だとします.
このとき”sts test var”と入れるとoverallの検定になりますが、オプションで”trend”と入れるだけで傾向検定の結果が得られるのです.楽ちんですね.
これを使っている研究は本当にたくさんあります.たまたま見つけたJAMAの論文(JAMA 2007; 298: 299-308)がわかりやすいので、見てみてください.
4.まとめ
いかがでしたか?傾向検定についてはアウトカムの種類に応じて整理していくととてもスッキリしますよね.
二値変数の割合:Cochran-Armitage trend testはptrend,
連続変数の平均:Jonckheere–Terpstra trend testはnptrend,
生存時間分析:Log-rank trend testはsts test var, trend
ということで整理ができたでしょうか.



コメント