生存時間分析を行う上で、カプランマイヤー法は一般的によく用いられる方法です.
生存時間分析を用いて研究を行うとき、打ち切りがランダムに発生する
という前提条件に基づいていますが、本当にそうなのかはわかりません.
今日は、何らかの理由に基づく打ち切りがどのように結果に影響するかをカプランマイヤーを用いて説明します.
1.カプランマイヤー法とは
カプランマイヤーとは、縦軸を生存割合、横軸を時間として、
実際の観測値に基づいた、経時的な累積生存割合の推移を示したものです.
イベントが発生した時点で存在する「at-risk集団(NT)」を分母とし、発生したイベント数(nT)を分子として、
その直前の時点での生存割合PT-1にかけ算することで、そのときの生存割合PTは以下の式で与えられます.
PT = PT-1 ×(1 – nT / NT )
イベントを発生せずに脱落した人は「打ち切り」として処理され、イベント数には関与しません.
ただしat-risk集団は少なくなるために(分母が減るために)イベント1つ起こることの影響が大きくなります
次に具体例に基づいてカプランマイヤーを描いてみることにしましょう.
2.カプランマイヤーの描き方
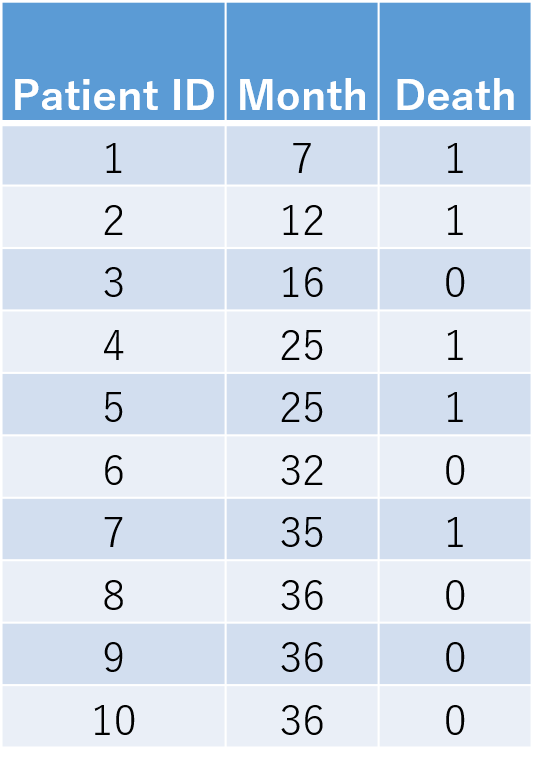
(問題)10名の患者を最大36ヶ月フォローしたところ、上の表のようになった
このとき、縦軸をSurvival probability(生存割合、生存確率)としてカプランマイヤーを描くとどのようになるか?
<ルール>
最初(t=0)は全員生存しているので、1からスタート
イベントが生じたとき、その時点でのat-risk集団におけるイベント発生確率を計算(打ち切り例は数えない)
前の時点の生存確率×(1ー死亡事象発生確率)で計算
以下の図のように描けるかと思います.

次に、少し特殊な状況を想定してみましょう.
まずは、打ち切りがいないときを想定してみます.
ここでは特に、打ち切られた人達が全員生存していると想定します.
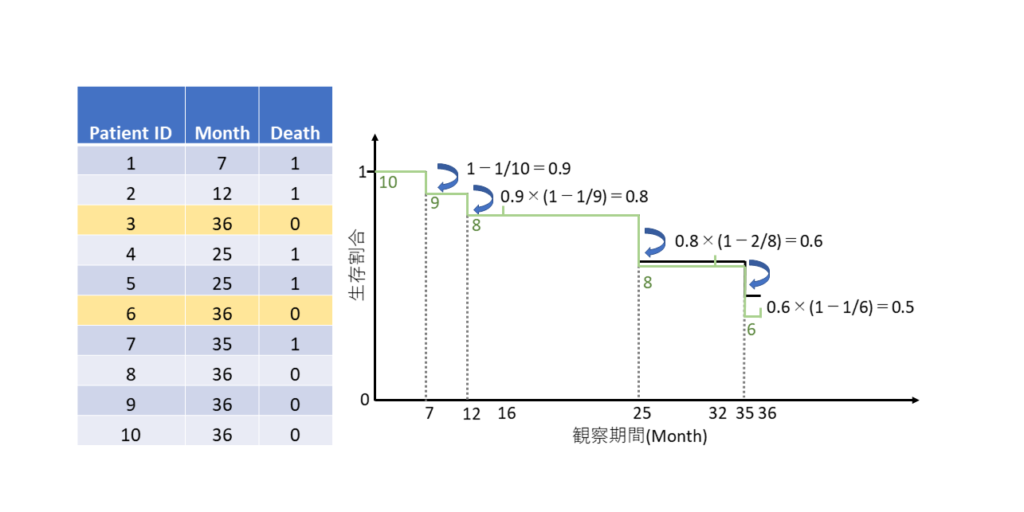
打ち切られた人がすべて生存していると、生存曲線は上にいきます
逆に言えば、打ち切りのせいで悪く見積もられてしまうことになります.
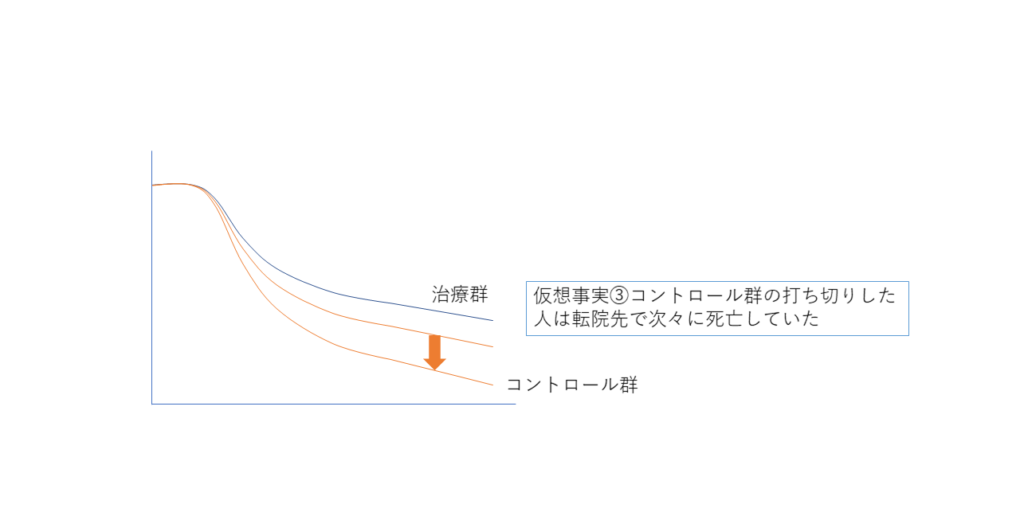
次に、打ち切りになっていた人が死亡していた場合はどうなるでしょうか?
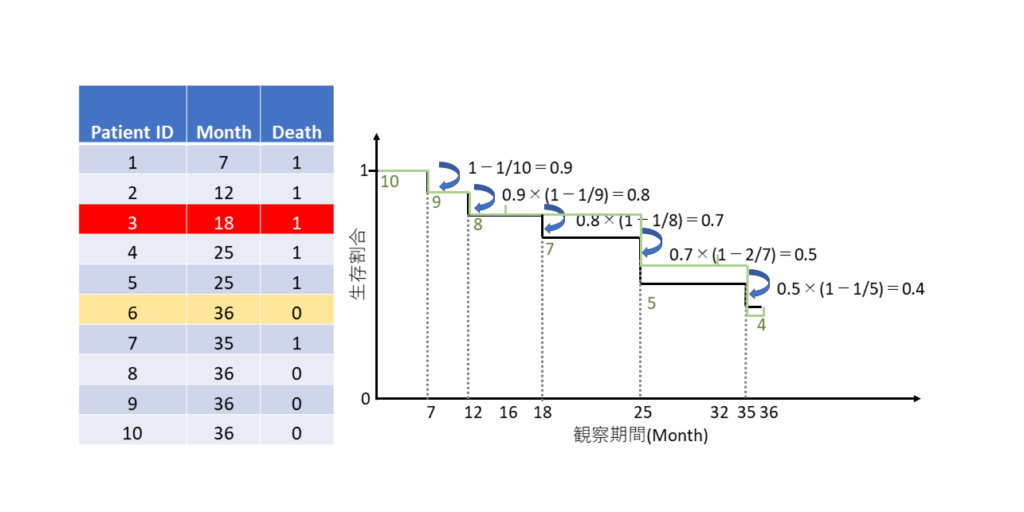
打ち切られた人が死亡していると、生存曲線は下にいきます
逆に言えば、打ち切りのせいで悪いはずの予後が、誤って「よく」見積もられてしまうことになります.
以上のことから、
・転院後にすぐ死亡 → 生存曲線は今よりも下にあるはず
・転院したがその後長らく生き続ける → 生存曲線は今よりも上にあるはず
転院した理由が病状とは独立していてランダムに発生する偶然の事象である
→ 生存曲線は今と変わらないはず
このように、コホート研究では、何事もイベントを生じなかった人も最後までできるだけしつこく追跡することが重要です.
3.カプランマイヤーで示すバイアス
生存分析におけるバイアスをわかりやすくいくつかシミュレーションしてみましょう.


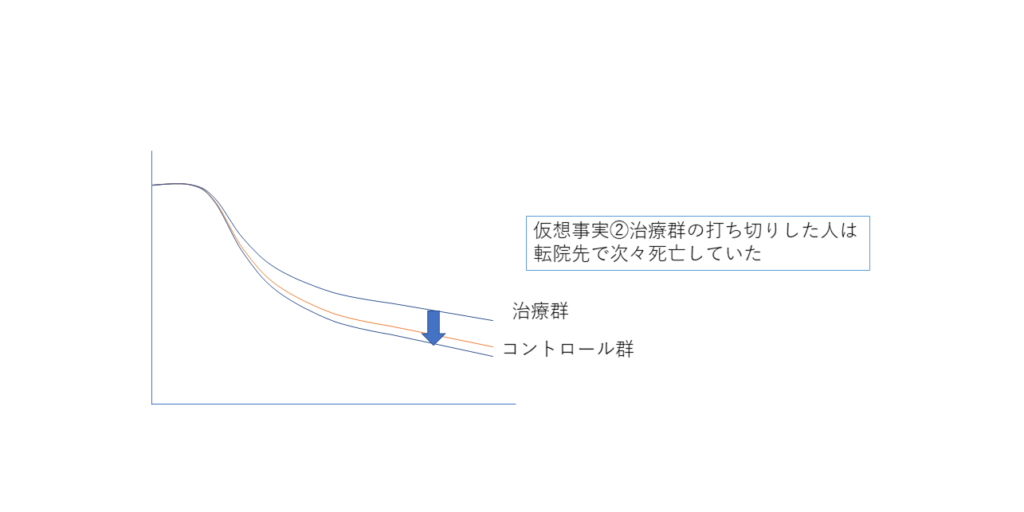

このようなバイアスは、差を縮める方向のバイアスがかかっているとき(bias toward the null hypothesis)、それにもかかわらず差を見いだせたときに、より頑健な結果であると主張することができます.
こうしたバイアスを逆手に取った主張というのは、疫学研究においては常套手段ですので、ぜひこの考え方に慣れておくとよいでしょう.
4.まとめ
カプランマイヤー法による生存曲線の描き方を通じて、生存分析におけるバイアスについて説明しました.
上手にBias toward nullを使いこなして、Discussionを充実させましょう.



コメント