時間関連バイアス（Time-related biases）①

今回も疫学に関する内容です．疫学の知識をもって統計やプログラミングを実践することを目指しましょう。．

今日のお話はバイアスに関することです．Rothmanでも何でも疫学の教科書では選択バイアス、情報バイアス、そして広義には交絡も含むことがありますが、今日お話する種類のバイアスは、こうした分類とは少し違った分類になります．無理矢理分類しようとすればそれぞれ選択バイアスとか情報バイアスに分類することができるのですが、敢えて「時間関連バイアス」という言葉で括って理解したほうがよりよく理解することができると思います．

※Penn大のIntroduction to Epidemiologyという授業内容を元にまとめています．

その授業では、時間関連バイアスには以下の4つがあるとしています．

1. Immortal time bias: 無イベント生存期間が存在することによるバイアス
2. Protopathic bias (reverse causality): 因果の逆転
3. Lead time bias: 早期発見によりイベントの生じにくい期間が存在することによる誤分類
4. Length time bias: 急激に悪化するような症例が除かれてしまう選択バイアス

そして、この時間関連バイアスの重要性は薬剤の有効性を示すような観察研究において特に重要な意味を持ちます．SGLT2阻害薬は2つのRCT（CANVASとEMPA-REG OUTCOME）とその後の2つの観察研究（CVD-REALとEASEL）で結果に違いが見られています．観察研究において心血管事象の抑制効果がより顕著に出ていること、新規使用開始者全体（RCTでは高リスク者限定だった）で効果あり、と結論づけられています．これが時間関連バイアスによるものの可能性が指摘されています．

However, time-related biases that are frequent in such observational studies of drug effects could have exaggerated the association between SGLT2i use and mortality. Immortal time bias is particularly important to examine in these studies.

Reduced Mortality With Sodium-Glucose Cotransporter–2 Inhibitors in Observational Studies
Avoiding Immortal Time Bias. Circulation 2018; 137: 1432

今回はそのうちの一つであるimmortal time biasについてじっくり解説します．

1．Immortal time bias

アカデミー賞を受賞した人はそうでない芸能人よりも長生きである

Redelmeier et al. Ann Intern Med. 2001

2001年のAnnals of Internal Medicine に掲載された論文です．平均寿命は79.7歳 vs. 75.8歳（P = 0.003）で年間で28％の死亡率減だったそうです.

皆さんはこれが怪しいと見抜けたでしょうか？

からくりとしてはこうです．「アカデミー賞を獲るまで生きていた」

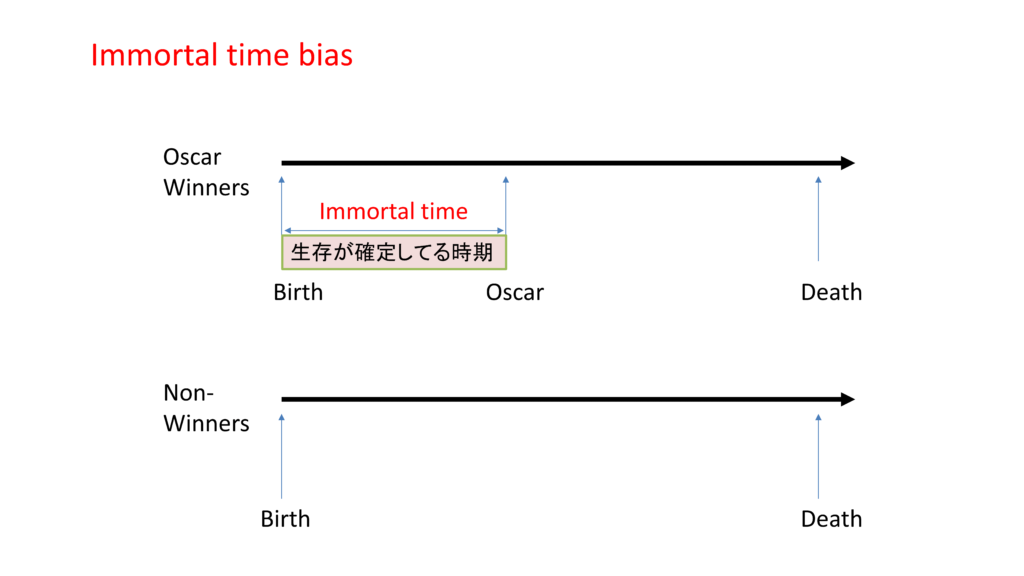
イベントを起こさずに生存していることが確定している場合、カプランマイヤーは下がり始めませんね．それがようやく下がり始めるのは受賞したという事実が確定してからになります．

事実こうしたバイアスが原因で結果が歪められていたことを認める論文が同じAnnals of Internal Medicine から出版されました．

“When the authors of the current article reanalyzed the data using methods that avoided this “immortal time” bias, the survival advantage was closer to 1 year and was not statistically significant.”

「やり直してみたら差はありませんでした」という結果。

Do Oscar Winners Live Longer than Less Successful Peers? A Reanalysis of the Evidence. (Ann Intern Med. 2006)

例えば新規の薬剤と切り替えたあとの予後を調べる、という場合にはこうしたバイアスの制御が必要になります．最初のアカデミー賞と合わせてこれらは誤分類バイアス（情報バイアス）になります．

あるいは、ある疾患に対して手術を行うことの有益性を示す研究をしたとします．診断から平均して4週間くらい経過してから手術を行うことが一般的だとすると、診断から手術までの4週間の間に不幸にして亡くなってしまった場合はどうなるか？その場合は非手術群になってしまいます．（こちらは選択バイアスになります）

こうしたバイアスは観察研究で起こりえます．特にデータベースを用いた大規模研究などのいわゆるリアルワールドデータでは注意が必要です．

前述の例であれば診断から4週間以内にイベントを生じた症例は解析しないとか、時間依存変数による解析、Nested case-control研究などの研究デザイン上の工夫で対処します．

具体的にどんな例があるのか、どのように対処すべきかはこの文献(BMJ 2010;340:b5087)がよく引用されていますので参考にしてみてください．

さて、冒頭のSGLT2阻害薬の例ですが、これまでにその他の糖尿病薬が使用されていた人がSGLT2阻害薬を使い始めるまでの期間がnon-SGLT2群に与えられないので不利だ、という主張でした．

こうしたバイアスはすべての観察研究につきものですので、RCTの結果よりも効果が大きく出たりすることは決して稀ではないのです．

ちなみにこの論文ではさらに次のようにimmortal time biasを避けることができると述べています．

Poisson-type regression techniques or Cox-type models with time-varying exposure that allow the proper classification of this immortal person-time. Alternatively, if the study requires matching on propensity scores such as the CVD-REAL and EASEL studies, a prevalent new-user design with time-conditional propensity scores can be used to avoid this bias.

時間依存exposureを考慮に入れたPoissonやCoxとか、prevalent new-user design with time-conditional propensity scoresをやると避けられる

Reduced Mortality With Sodium-Glucose Cotransporter–2 Inhibitors in Observational Studies
Avoiding Immortal Time Bias. Circulation 2018; 137: 1432

単純にimmortal timeを飛ばす、あるいは除外すればいいのだとばかり思っていましたが、controlとtreatmentがしばしばcrossoverするような現実世界のデータ解析ではもっと慎重になるべきなのでしょう．同様のことがこちらの論文にもあります．除外が最も効果を（誤って）過大評価していたということでした．

こうした疫学上の知識無しにはリアルワールドデータを使った薬剤の効果を推定する研究はおぼつかないですね．

次回は残りの時間関連バイアスについて解説します．