プログラムにミスが見つかりましたので訂正いたしました。お知らせくださった先生、ありがとうございます。(2022/7/8)
前回、前々回の記事では競合リスク解析の理論と実践の初歩について説明しました.今回はちょっとした応用編です.
前回の記事でもお伝えしましたが、Stataでは競合リスクを考慮したCumulative incidence法でのグラフを描いて必要な統計的な検討を一発で済ませるコマンドが存在しません.
前回の記事ではDo-file上にプログラムを作成してグラフを作り出す過程を示しましたが、今回は少しだけ応用を利かせたグラフをご紹介します.
Kidney Transplantation Outcomes across GN Subtypes in the United StatesJ Am Soc Nephrol (2017; 28: 632–644)
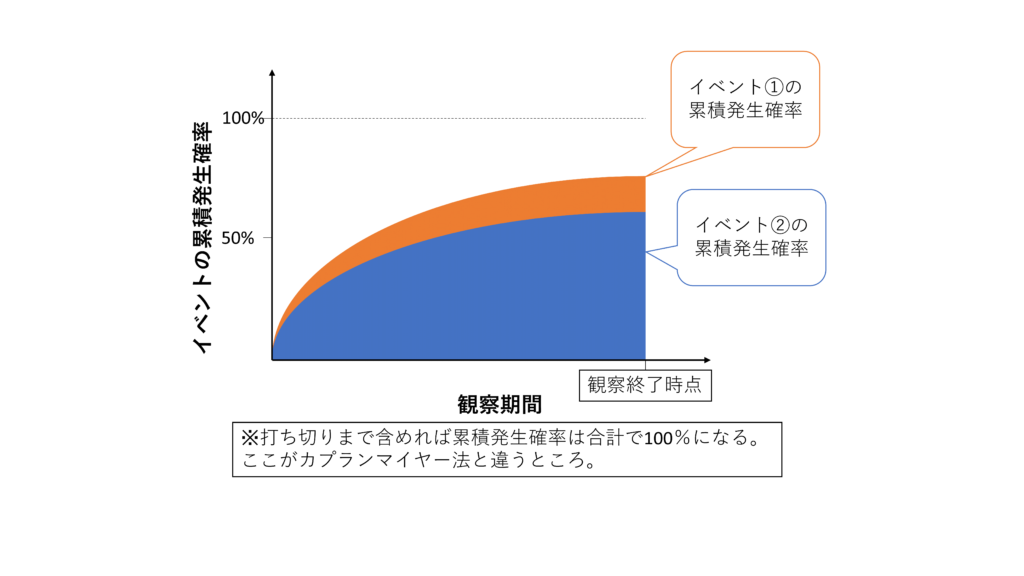
の論文にあるグラフが非常に印象的で、何とかまねできないかと考えていました.
コピペして紹介したいのですが、さすがに道義上できませんので、イメージ図だけ貼り付けておきます.(ただし論文はフリーですので是非覗いてみてください!Figure 2です.)
*** 活用するデータセット
webuse hypoxia, clear
*** 生存時間分析宣言
stset dftime, failure(failtype==1) 
ここでfailtype = 2を競合リスクイベントとします. メインの曝露因子をpelnodeとします.
生存時間分析をするという宣言をするところまでは一緒ですが、ここであらたに”stcompet”でcumulative incidence functionを定義します.
### Syntax ###
.stcompet newvarname = { ci | se | hi | lo } [[newvarname = ...] [...] ] ///
[if exp] [in range] , compet1(numlist) [compet2(numlist) compet3(numlist) ///
compet4(numlist) compet5(numlist) compet6(numlist) by(varname) allignol level(#) ]
/// 競合イベントを6つまで定義可能, byの中に曝露因子/介入因子を入れる
/// ci: cumulative incidence function
/// se: standard error of the CI
/// hi: 信頼区間上限 <- ln[-ln(Cumulative Incidence)]
/// lo: 信頼区間下限 <- ln[-ln(Cumulative Incidence)]
/// level: 信頼区間のレベルを規定.Defaultでは95%興味のあるイベントが「1」、競合イベントが「2」とした場合には以下のようになります.ポイントとしては、片方をCompositeにするということです. これならグラフを積み重ねることができます.
*** 競合リスクイベントを定義
stcompet cif = ci, compet1(2) by(pelnode)
*** ここで曝露因子を持つ群における興味のあるイベントの累積発生確率を計算
gen cif_ev1_exposure = cif if failtype == 1 & pelnode == 1
drop cif
*** さらに競合イベントとのcomposite outcomeのCIFを計算
stset dftime, failure(failtype==1 2) /// compositeにする
stcompet cif = ci, compet1(0) by(pelnode)
gen cif_ev2_exposure = cif if (failtype == 1| failtype==2) & pelnode == 1 2022/7/8にご指摘いただいたのは、赤字部分で、failtype==2となっておりました。これのせいでネイビー色のグラフが中途半端な長さになってしまったようです。
これを元にしてグラフを作成します
#delimit;
twoway
(area cif_ev2_exposure _t, sort bcolor(navy))
||
(area cif_ev1_exposure _t, sort bcolor(maroon))
,
ytitle(Cumulative Incidence)
;
#delimit cr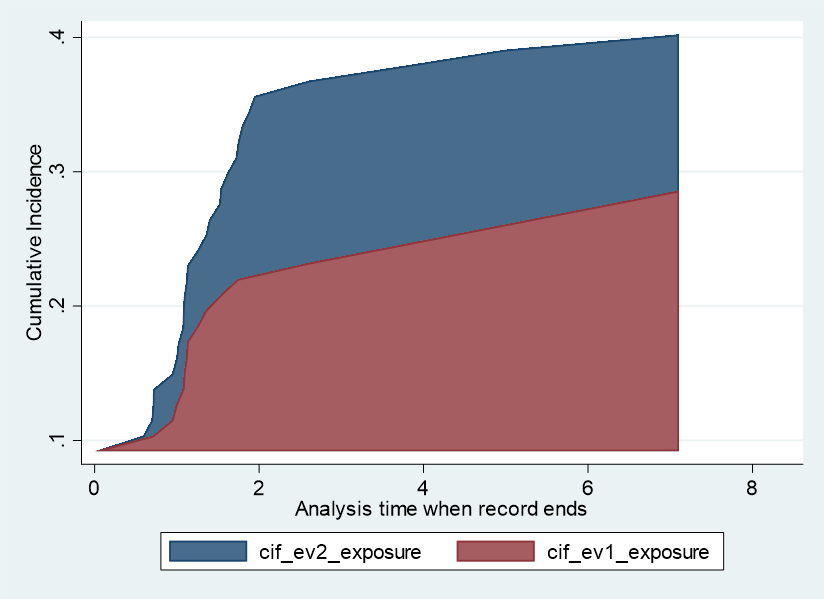
このグラフですと、最初のスタート地点と最終観察地点が美しくないデスね.何が問題なのでしょうか?
- スタートがゼロから始まっていない
- 最終観察地点までグラフが延びていない
スタートが一段上がったところからスタートしているのには理由があります.観察開始早々から打ち切りイベントが生じてしまっていることが挙げられます.

さらに、観察終了までに8.4年ほどあるはずなのですが、7年程度のところでグラフが切れてしまっています.
CIFはイベントが生じない限り値が計算されません.そのことに起因するものと思われます.
なので、よそ行きのグラフに仕立て上げるには、少々細工を施す必要があります.
*** 最初をゼロ始まりにするためにダミーのIDを1つ生成する
set obs `=_N+1'
count
replace pelnode = 1 in `r(N)'
replace stnum = 1000 in `r(N)'
*** 競合リスクイベントを定義
stset dftime, failure(failtype==1)
stcompet cif = ci, compet1(2) by(pelnode)
*** ここで曝露因子を持つ群における興味のあるイベントの累積発生確率を計算
gen cif_ev1_exposure = cif if failtype == 1 & pelnode == 1
** 観察終了まで横に線を延ばす. 最も高いCIFを観察の終わりまで延ばす
sum cif_ev1_exposure
local m = r(max)
gsort pelnode -_t
bysort pelnode: gen flg = _n
replace cif_ev1_exposure = `m' if flg==1 & pelnode==1
drop cif flg
*** さらに競合イベントとのcomposite outcomeのCIFを計算
stset dftime, failure(failtype==1 2)
stcompet cif = ci, compet1(0) by(pelnode)
gen cif_ev2_exposure = cif if (failtype == 1| failtype==2) & pelnode == 1
** 観察終了まで横に線を延ばす
sum cif_ev2_exposure
local m = r(max)
gsort pelnode -_t
bysort pelnode: gen flg = _n
replace cif_ev2_exposure = `m' if flg==1 & pelnode==1
*** ゼロを出発点にする
replace cif_ev1_exposure = 0 if stnum==1000
replace cif_ev2_exposure = 0 if stnum==1000
replace _t0 = 0 if stnum==1000
replace _t = if stnum==1000
*** グラフ作成
#delimit;
twoway
(area cif_ev2_exposure _t, sort bcolor(navy))
||
(area cif_ev1_exposure _t, sort bcolor(maroon))
,
ytitle(Cumulative Incidence) ysc(range(0 0.6)) ylabel(0(0.2)0.6, ang(0))
legend(order(2 "Event 1" 1 "Event 2") col(1) ring(0) pos(1))
;
#delimit cr 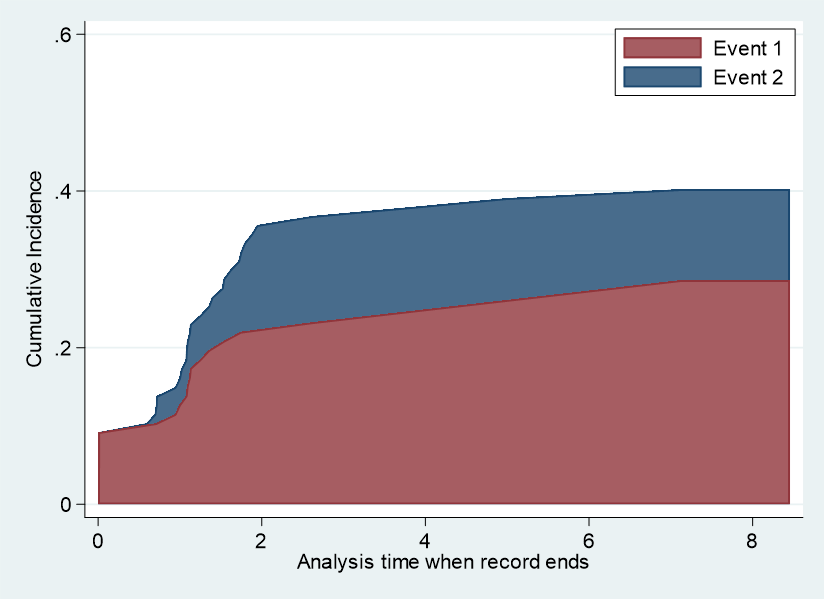
これできれいに最初から最後まで、ゼロを出発点としたグラフが描かれました.
まとめ
Stataで競合リスクを考慮したCumulative incidence法で競合するイベントごとの累積確率を重ねるグラフを作成しました.これをExposureの種類に応じて比較してグラフを並べるときれいですね.



コメント
いつも参考にしております。
Rですとggcompetingrisks()を使えば上記グラフが一発で作成されるので便利です。
ありがとうございます!Rでは簡単にできることがStataでできなかったりってのが結構あるので、使い分けができると便利ですよね。