このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回は皆さんもお馴染みの、母平均の検定でよく使われる t検定について、その前提条件なども考えながらマニュアルで実行することで理解を深めていきたいと思います.
t検定は1標本か独立した2標本の平均値を比較するのに用いられます.
標本の分布は、母分散が既知なのか未知なのか、そして標本の大きさがどの程度なのかによって異なることを前回の記事で説明していますが、平均の検定においては多くの場合、標本数がそれほど大きくなく(30未満)、母分散は未知であるため、t検定を用いるのが基本です.
1.t検定の流れと前提条件
t検定は標本の数によって分類されます.1標本か2標本です.
1標本の場合は、未知の母平均μを別のところから求めてきた母平均μ0と同じかどうかを比較するのに用います.
手順としては、
- 未知の母平均μは、標本平均xを用いて求める.
- 母分散σ2も未知として標本分散s2を求める.
- 検定統計量(この場合はt値)を求める.
- 帰無仮説の元でその検定統計量が得られる確率(p値)を求める.
- 得られたp値が帰無仮説棄却域に入るならば帰無仮説を棄却する.
というながれになります.
このときに必要な前提がいくつかあります.
- データは連続変数である.
- データは母集団からランダムに抽出されてきた独立したデータである.
- データの分布は正規分布かそれに近い分布である.
- 2標本で平均値の検定を行う場合、その2標本の母分散は等しい.
2.1標本のt検定
母平均がわかっているような状況で、あるサンプリングデータを目の前にしたとき、そのサンプルにおける標本平均が、母平均と乖離しているのかどうかを調べる方法になります.
例1)会社に勤めている人全員の収縮期血圧の母平均が120mmHgとわかっているとした場合.自分の所属する部署はストレス過多で血圧が高い高いと口々に言っていたとします.その部署内でランダムに9人選んで血圧を測定したところ、平均130mmHg、標準偏差は10mmHgという結果が得られたとします.この部署の人達は他の部署に比べて血圧が高いのでしょうか?
以下の様な数式を用いてそれぞれの値を求めることになります.

今回の状況においては x や s はすでに求まっているので、t値を求めることになります.
ということで、
t = (130 – 120)/(10÷√9)=3
と求まります.
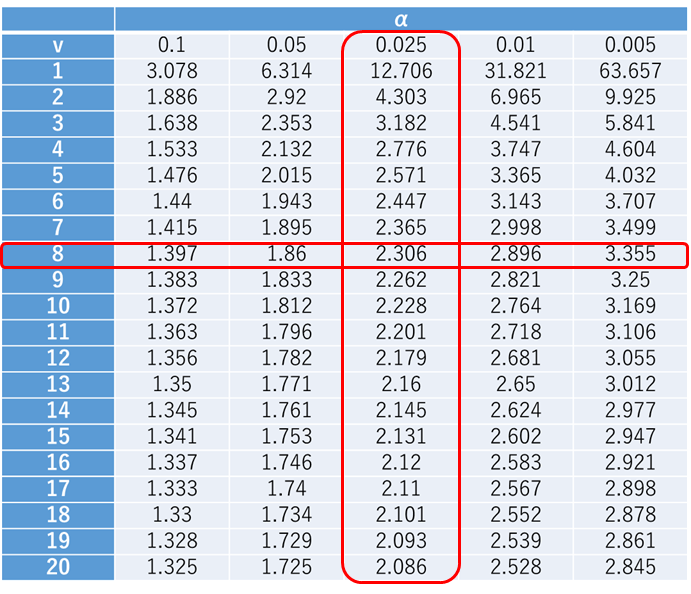
自由度n -1のt分布に従うので、自由度は8となりますので、両側検定だとするとこの場合は2.306よりも大きければ帰無仮説は棄却されることになります.
また、95%信頼区間は以下の式で与えられます.
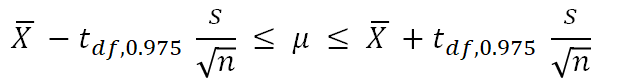
この場合のt値は2.306ですので、2.306×10/√9 を計算してXに±すれば求められますね.
3.対応のあるt検定
対応のあるt検定は、独立していない2データの差が0であるという帰無仮説を検定します.
2データの差をとることで、1つのデータにしてから平均値を求めて1標本のt検定を行うことになります.以下の例を用いて説明します.
例2)ある刺激を加えると前後で血圧が上昇するかどうかを検証する実験を行っており、10人の被験者で実施したところ、以下の表に示す結果が得られたとします.
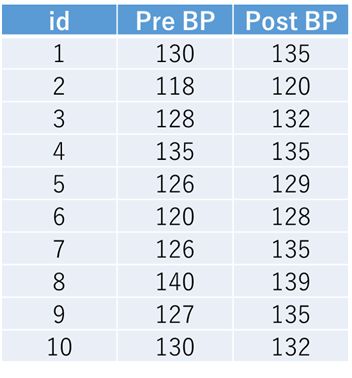
これはStataで実施する場合、
input id preBP postBP
1 130 135
2 118 120
3 128 132
4 135 135
5 126 129
6 120 128
7 126 135
8 140 139
9 127 135
10 130 132
end
ttest preBP = postBP
結果はシンプルに出力されます.片側検定ならば左のPr(T<t)=0.0027を用いればよいですし、両側検定ならPr(|T| > |t|) = 0.0053となるわけです.
もう少し詳しくみてみると、preBP, postBP, diffとでてきます.このdiffは、2つのデータの差を示します.これが0と一緒のことですよね?というのが帰無仮説なわけです.
差の分散は、

の式から手計算で求める必要がありますが、不偏分散となるためn-1で割った値になることに注意してください.
こうして求められたt値が3.6515ということで、自由度9のt分布で片側/両側の棄却域に入っているかを検定します.片側の場合にはt=3.6515が示すよりも上の部分の確率を片方だけ計算すればよいですが、両側はその2倍になることに注意してください.
手で計算するとした場合は以下の様になります.(まあ、正直な話、どこまで細かくやるかなんですけどねぇ.)
input id preBP postBP
1 130 135
2 118 120
3 128 132
4 135 135
5 126 129
6 120 128
7 126 135
8 140 139
9 127 135
10 130 132
end
gen delta = postBP - preBP
egen meandelta = mean(delta)
egen s = sum((delta - meandelta)^2)
gen ssquare = s/9
local t = meandelta/(sqrt(ssquare/10))
disp ttail(9, `t') /* 片側検定のみの結果 */
disp 2*ttail(9, `t') /* 両側検定の結果 */これをローカル変数に格納すればプログラムを組んで自分の好きなように表示することができます.
なお、信頼区間を出す際に、t値を求めるのにinvt() という関数を使うとよいです.
両側検定を行う場合、自由度9、棄却域0.975で設定するとそのときのt値がでますので、
local t = invt(9, 0.975)
local lb = meandelta - `t'*(sqrt(ssquare/10))
local ub = meandelta + `t'*(sqrt(ssquare/10))
disp %4.3f `lb', %4.3f `ub'
.1.522 6.478こんな感じで信頼区間がついて結果が、4.0 [1.52 to 6.48] と表せることがわかります.
このように、マニュアルで行う方法にも精通しておいた方がプログラムを書く上で非常に役立つと思いますので、ぜひこれらの方法を押さえてみてください.(上記プログラムももっと上手に綺麗にやる方法があると思うので…)
4.独立する2標本のt検定
この場合にはt検定を実施するために必要な条件が1つ加わったわけですが、それは、
等分散であること
です.とはいえ標本平均も標準偏差もそれぞれに計算する必要があります.
そして、最終的には別々に計算した標準偏差を元にして分散を統合した1つの値にする必要があります.
このとき自由度は、(n1 – 1)+(n2 – 1)=n1 + n2 – 2 であり、その自由度におけるt分布に従うとして計算を進めていきます.
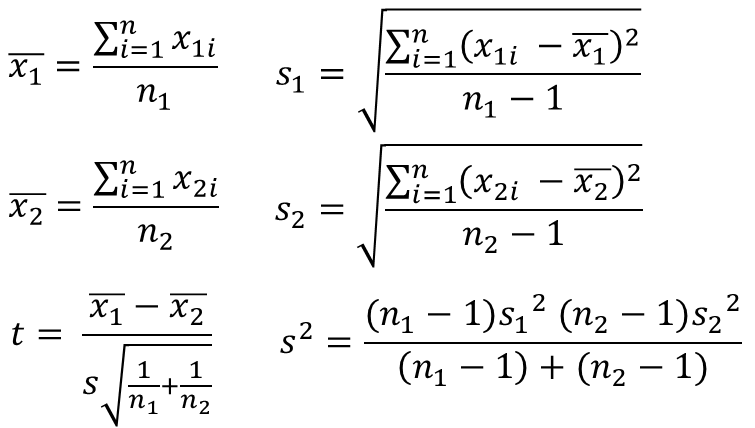
分散はそれぞれの分散について自由度の加重平均をとっている、と理解すると覚えやすいでしょうか.
ここでサンプルデータを使って前提の確認とt検定をStataでやってみましょう.
import delimited "sampledata_ttest.csv", clear
histogram var, by(group)
qnorm var if group==1
qnorm var if group==2
* Check equality of two variances
sdtest var,by(group)
* Two sample t-test for equal variance
ttest var, by(group)まずは視覚的に値の分布を確認します.(ヒストグラム)

まあまあ左右対称で釣り鐘型のデータに分かれているように見えますね.
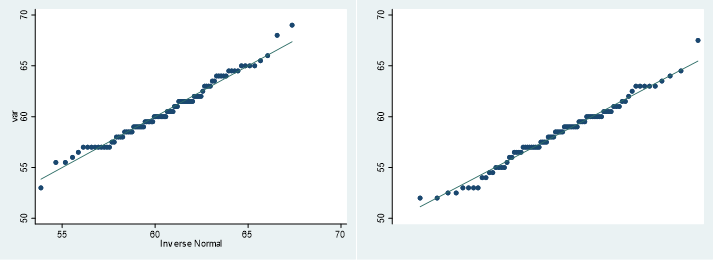
QQplotも正規性ありという感じです.
普段はここまでやらないかな~と思いますが、等分散性の確認をします.
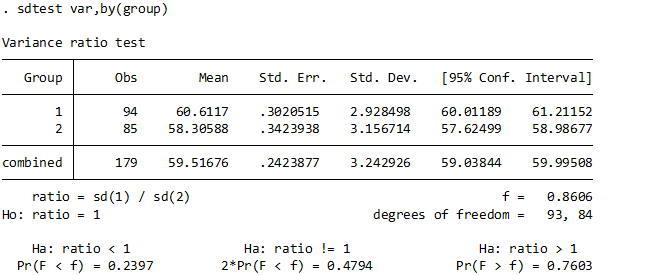
これはつまるところがF検定を行って等分散性をみています.
ratio = sd(1)/sd(2)と書いておきながら実際にはそれぞれの二乗の比を取るF検定をしています.
ちなみにF値は「両群の分散の比」と覚えましょう.分子と分母の自由度がクロスするところ値よりもF値が大きければ棄却域を超えるため「等分散ではない」ことになります.
したがって解釈としては、P値が0.05未満とならなければよいので、OKです.
そして最後はt検定です. この部分は手計算使用とすると計算量が多いので割愛.
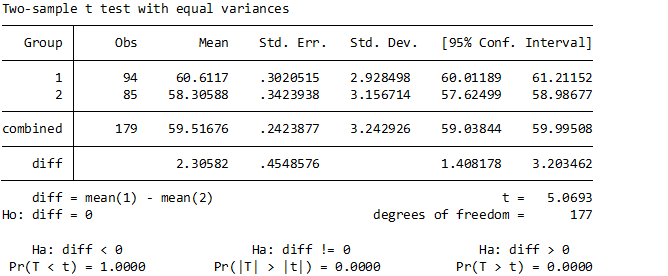
上記の公式に当てはめて実施してもらっても結構ですが、まあまあしんどいですよね…。
まとめ
普段何気なくやっているt検定ですが、土台の部分をきちんと理解した上で用いるとさらにもう一歩先に進めるのではないかと思います.



コメント
[…] 以前の記事で独立した2群間での連続変数の平均値の検定をt検定で行いました. […]