どのソフトで計算するにしても、プログラミングを行って統計量や検定結果を自分の好みの形で出力するためには統計学の基本的な知識はどうしても必要になります.
統計学をまじめに勉強すると奥が深いのですが、今日は、
「P値の計算式をどうやってプログラムに組み込むか」
を目標に、それに必要な最低限の統計学について整理してみます.
| 本日の内容 1.統計のざっくりとした分類 2.標準正規分布、t分布について |
1.統計のざっくりとした分類
統計には記述的な統計(descriptive statistics)と推定的な統計(inferential statistics)に分けて論じることが多いのですが、
前者は、得られたサンプルを構成するデータの特徴を表現するためのモノです.
具体的には平均値や中央値といった代表値や値の分布を表現したり、グループごとに比較したりする際に用いられます.
得られたサンプルの大部分はこの範囲に収まっている、という解釈をします.
後者は、理想的な集団(=母集団、population)の特徴を、母集団から得られたデータ(標本、sample)から推測(推定)することを指します.
限られた標本から調査したい母集団全体の特徴を推測するというものです.
このとき、得られたサンプルをもとに点推定および区間推定(信頼区間と呼ばれるもの)を求め、仮説検定を行います.
ここで表される信頼区間は、例えば95%信頼区間ということであれば、
母集団からサンプリングを100回行って、真の値(母集団における本来の値)を含む推定をしたら、ある値の範囲に95%の確率で収まった.
ことになります.
下記のようなイメージになります.
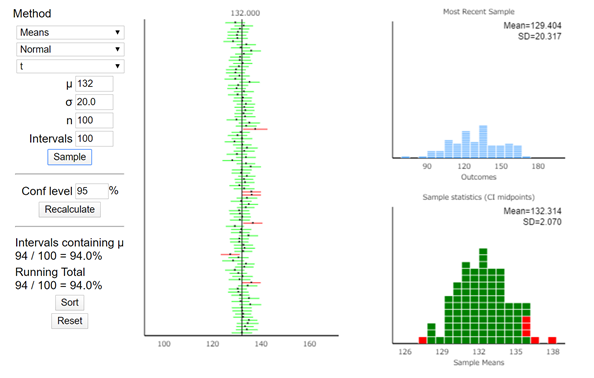
次に、仮説検定を理解するためには、次に「値の分布」に関する知識が必要になります.
2.標準正規分布、t分布について
標準正規分布は平均0、分散1の釣り鐘型左右対称の、下の図のような曲線を描きます.
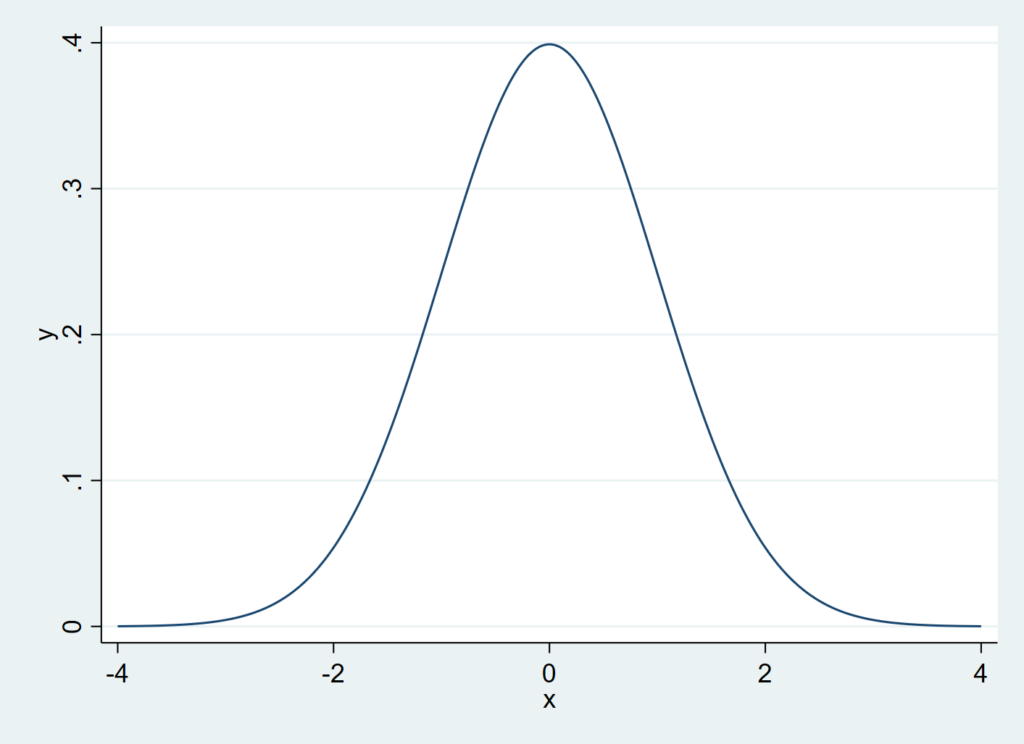
t分布は標準正規分布とよく似た形の分布で、パラメータである「自由度」によって分布の形が変わるという特徴を持っています.
自由度が大きくなるにつれて、標準正規分布に近づきます.
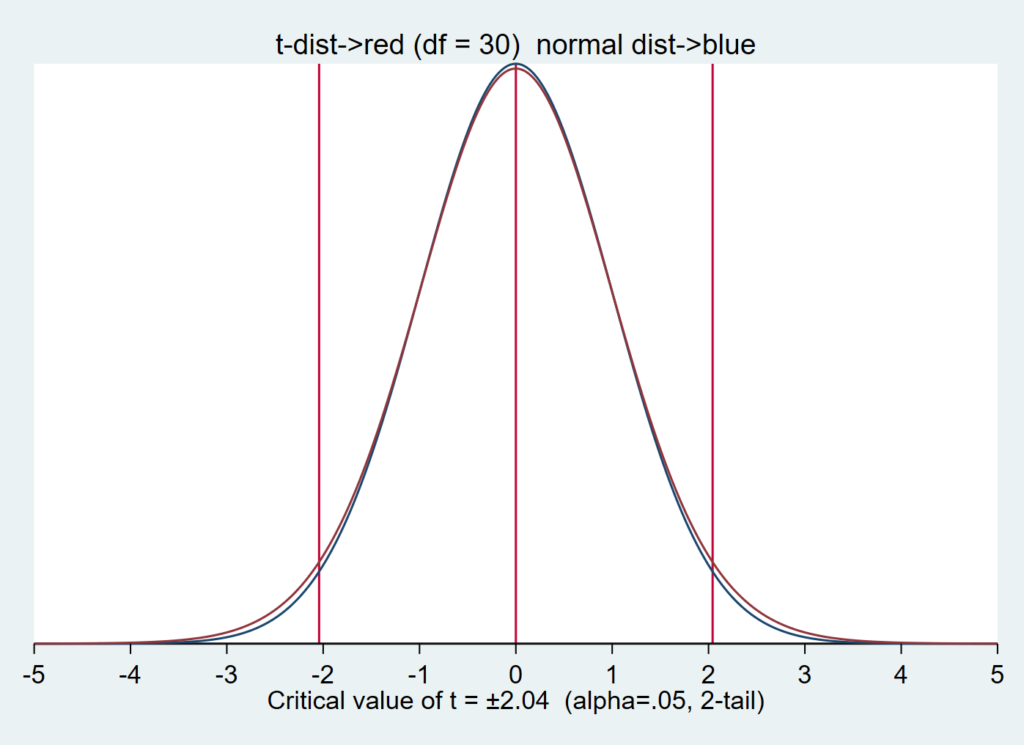
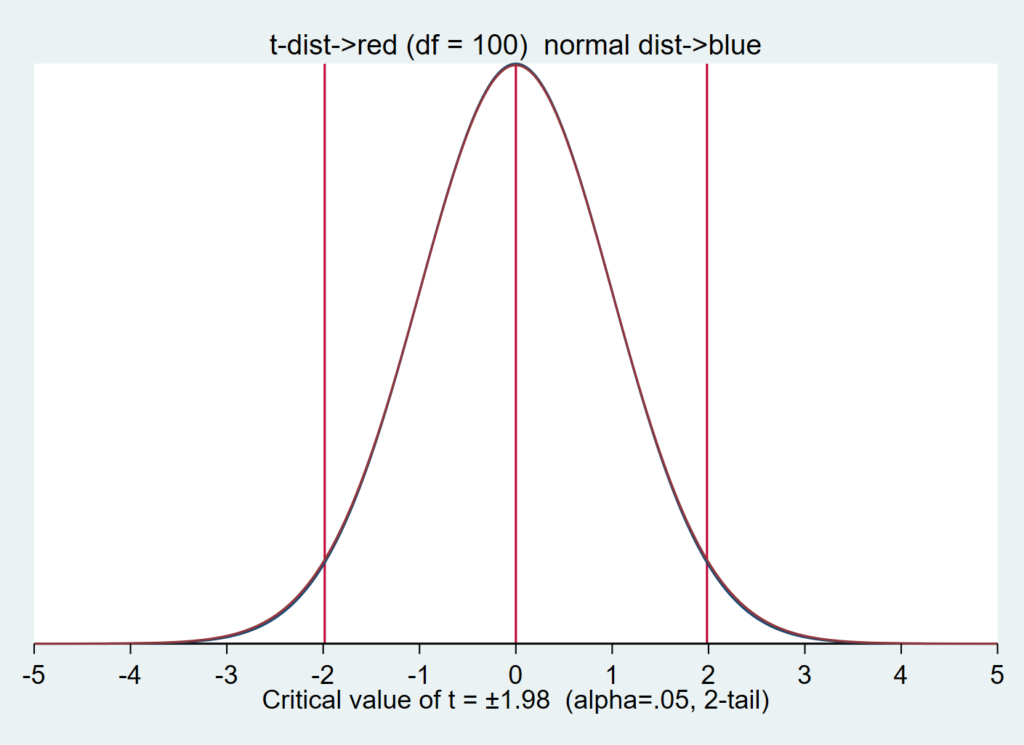
この分布は、もともと母集団から限られたサイズのサンプルを抽出して統計を行うことを目的として生み出されました.
t検定というのは、このt分布を用いて行いますが、記述統計の検定であるパラメトリックな連続変数の平均値の検定でよく使われています.
記述統計だけど推定的統計の要素が入っている、というので若干戸惑いますが、逆にいえば、このt検定がその後の統計学の発展に大きく寄与した、その入り口を見ている、ということなのでしょう.
さらにt分布、中心極限定理など詳しくお知りになりたい方はこちら.
まとめ
統計学は、記述統計と推測統計に分けられる.
t分布は、限られたサンプルから全体の結果を推定する方法.
次の記事では具体的にプログラミングに落とし込む流れを紹介してみたいと思います.



コメント