このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回は線形回帰の理論と回帰診断についてまとめてみました.参考にしたのはUCLAのサイトです.
1.線形回帰分析とは?
線形回帰とは、原因を表す説明変数(独立変数)、結果を表す目的変数(従属変数)から回帰式という直線を推定することをいいます.
対等な変数間の直線的な関係を調べたい場合には相関係数を求め、変数間の因果関係(実際には因果関係を推定する行為以上にはなりませんが)を想定している場合には回帰分析を使って変数間の関係を求めます.
線形回帰は、以下の様な式で表されます.
yi = α + βxi + ei
ここでyは目的変数、xは説明変数であり、iが付いているので、i番目の標本における目的変数と説明変数の関係性を表しています.eiは誤差項、αは切片、βは傾きを表します.
回帰式から予測した目的変数をyhat(yの頭に山形の記号が乗っているやつです)といい、実際の変数との差を残差といいます.
ここからは前述の誤差を残差と置き換えて考えてください.
2.線形回帰分析の前提条件
線形回帰分析の前提は最も簡単に覚えるならばLINEのacronymです.
- Linearity: 線形性.目的変数と説明変数の間が線形の関係であること.
- Independence: 独立性.これは、どの説明変数の残差間にも相関がないという前提.
- Normality: 正規性→誤差が正規分布していること(目的変数や説明変数自体が正規分布であることは必須ではない)
- Error variance: 誤差分散の均一性、あるいは等分散性.これだけではacronymとしてはやや苦しいですが、正確にはhomogeneity of variance, homoscedasticity などと表記されています
UCLAのサイトには、以下のようにまとめられています.
Linearity – the relationships between the predictors and the outcome variable should be linear
Normality – the errors should be normally distributed – technically normality is necessary only for hypothesis tests to be valid, estimation of the coefficients only requires that the errors be identically and independently distributed
Homogeneity of variance (homoscedasticity) – the error variance should be constant
Independence – the errors associated with one observation are not correlated with the errors of any other observation
Errors in variables – predictor variables are measured without error (we will cover this in Chapter 4)
Model specification – the model should be properly specified (including all relevant variables, and excluding irrelevant variables)
REGRESSION WITH STATA CHAPTER 2 – REGRESSION DIAGNOSTICS
よくある誤解に、回帰分析の説明変数や目的変数が正規分布していなければならない、というものがありますが、これは正確には、「残差の正規性」が問題なだけです.
これは回帰分析を行う際に、有意性の確認に使う分散分析のF検定の検定統計量の分母に該当するためで、F分布は分母・分子共に正規分布していなければならないからです.
3.最小二乗法とは
散布図に綺麗に引かれた回帰直線がありますが、この直線はどのように決まるのでしょうか?
それはこのグラフのように、予測されたyの値と実際の値の差である「残差」、これの二乗を足したものを最小にする、という風にして求めます.
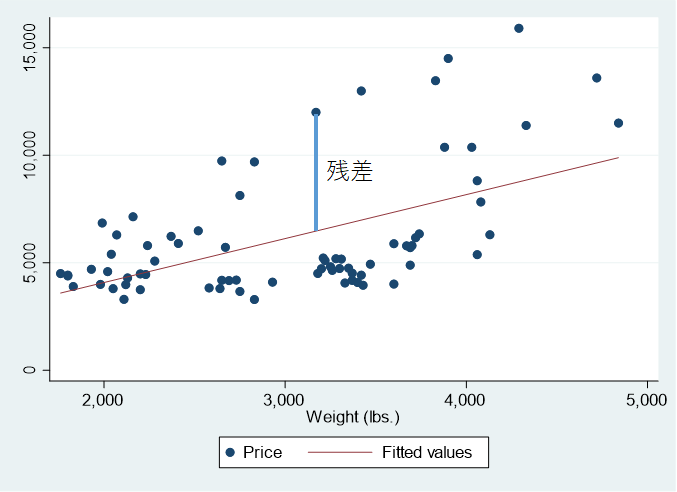
そしてどうして最小二乗法という方法がとられるのでしょうか?
それは一言でいえば「数学的に求めやすいから」です.マイナスの値をとらないようにするなら絶対値をとることだって可能なわけですが、ここで敢えてそうしないでしかも二乗にする、というところにミソがあるのです.
詳しい解説を字面ばかりで追ってもなかなか理解しづらいのですが、最近ではいろいろな動画がありますので、そちらをみて勉強するとはやいですね.
さて、平面上の直線というのは、y= ax + b のうちのaとbが決まれば1つに決まりますので、それを残差の二乗和の式から求めます.

この式で与えられる残差は、aとbに二変数関数ですので、それぞれの変数において偏微分した式を「0」として連立方程式を作って求めればよいわけです.
詳しい計算過程は動画で確認していただくとして、最後にa, bはそれぞれデータから計算できる値で計算可能な形に落ち着いていることがわかります.
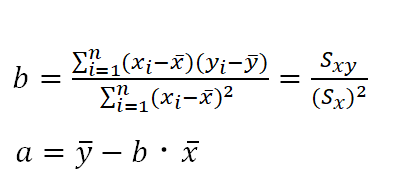
bについては、分子がxとyの共分散、分母がxの分散であることがポイントです.
ここで、相関係数の場合はどうだったでしょうか?
相関係数の場合は、bに相当するrを求める式が、xとyの共分散÷xとyそれぞれの標準偏差の積となっていました.
4.線形回帰の前提確認
前述のように線形回帰を当てはめるためには前提を満たしているかどうかを確認する必要があるでしょう.
一番手っ取り早い方法は、残差プロットで線形回帰の当てはまりを確認することです.また、外れ値などの極端な値によって全体の結果が影響を受けていないかも確認しておく必要があります.
最低限押さえたほうが良い回帰診断としては以下のような項目があります.
- 残差の分布の正規性を確認 … 図(ヒストグラム)と統計学的検定
- 残差の分散均一性の確認 … 図(残差対推定値プロット)と統計学的検定
- 影響力解析(外れ値の影響をみる)… てこ比
まずはサンプルデータを使って散布図と回帰直線を求めてみましょう.
webuse lbw2, clear
describe /* 変数名、ラベルなどを表示 */
twoway (scatter bwt lwt)
twoway (scatter bwt lwt)(lfit bwt lwt)
もう少し上手に書くとこんな感じで回帰係数を式に入れたりできたのでした.
regress bwt lwt
local B: dis %5.2f _b[lwt]
local C: dis %5.2f _b[_cons]
twoway (scatter bwt lwt)(lfit bwt lwt), legend(off) text(4100 210 "Y=`B'X+`C'")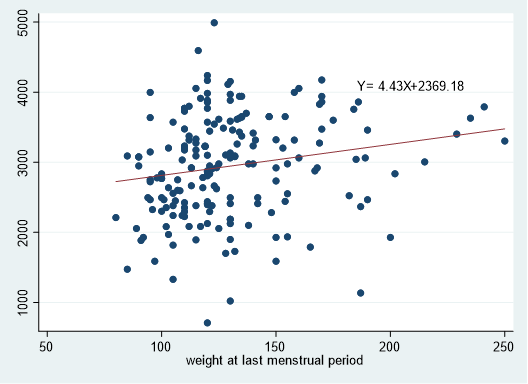
さて、ここから回帰診断をしてきます.
1)残差の正規性
まずは残差の正規性から確認していきましょう.
predictコマンドを使うとβhatだけでなく残差(residuals)も計算してくれます.図的にヒストグラムで確認しつつ、
regress bwt ui lwt smoke
predict bwthat, xb
predict r, residuals
hist r, normal
// 残差の正規性確認
sktest r
// 正規性は統計検定でも求められる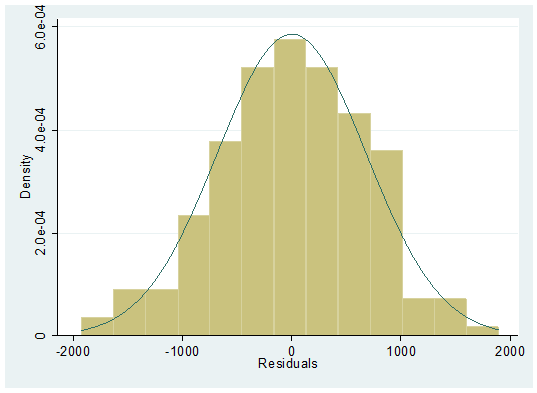
見た目にはきれいな釣り鐘型に見えますね.
2)残差の分散均一性の確認
次に残差の等分散性について確認します.
rvfplot, yline(0)
// 残差の分散均一性の検証.
hettest
// hettestが0.05以上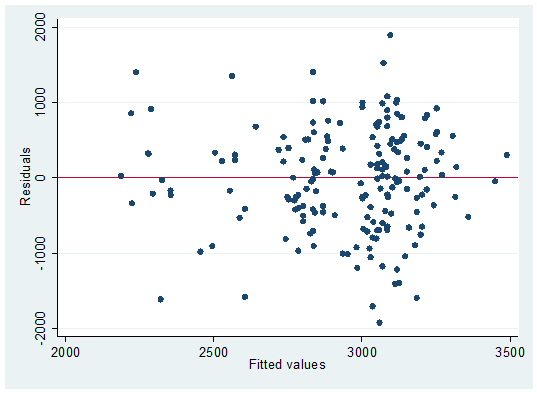
これをみると横軸に平行な残差=0を通過する直線を挟んで上下にバランスよくランダムに分布していることがわかります.
3)影響力解析(外れ値の影響をみる)
特定の外れ値の影響を受けていないかを確認します.
predict l, leverage
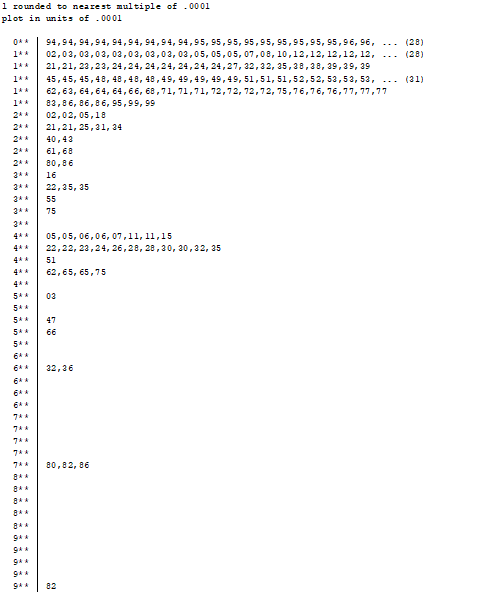
// 幹葉図を表示
stem l
gsort –l
//大→小へ並べ替えて
list id bwt lwt ui smoke l in 1/5
//大きい者5つを表示(0.1未満であれば影響力は小さい)
lvr2plot, mlabel(id)
// てこ比をプロットで確認.
UCLAのサイトにはその他にももりだくさんで、回帰診断についてのコマンドが紹介されていますので、時間があれば一読するとよいでしょう.



コメント