P値を計算する方法　②　各種検定・回帰モデルにおけるP値計算方法のまとめ

検定や回帰モデルを実施したあとに、P値や推定値を取り出す、という技があると、
表記方法をカスタマイズしたり、結果だけを手早くコピーしたりできるので、
その後のデータ整理の時間を短縮することができます.

特にたくさんのモデルを試した際に、結果だけとにかくコピーしたい！
という場合にはmacroをうまく使うと楽することができます.

1．χ2検定、t検定、Wilcoxon rank-sum testのP値の取り出し方

χ2検定、t検定、Wilcoxon rank-sum testではこれらの検定を行った直後にscalar値であるr(p) として一時的に格納されます.

これをすかさずマクロで定義してしまえばよく、

.tabulate y x, chi2 
.local p = r(p)
.disp %4.3f `p' 

とすればP値が得られます.

2．Kruskal-Wallis test、oneway ANOVA testのP値の取り出し方

ところが、３つ以上のグループでの検定を行うKruskal-Wallis testやoneway ANOVA testでは、計算が必要になります.

.kwallis var, by(group)
.display "P=" 1 - chi2(r(df), r(chi2))
.oneway var, by(group)
.display "P=" 1 - chi2(r(df_bart), r(chi2bart)) 

ここで、r(df)やr(df_bart)は自由度を表し、r(chi2)やr(chi2bart)はχ2値を表します.

χ2分布(自由度，χ2値)　

とすると、与えられた自由度、χ2値の確率を示します.

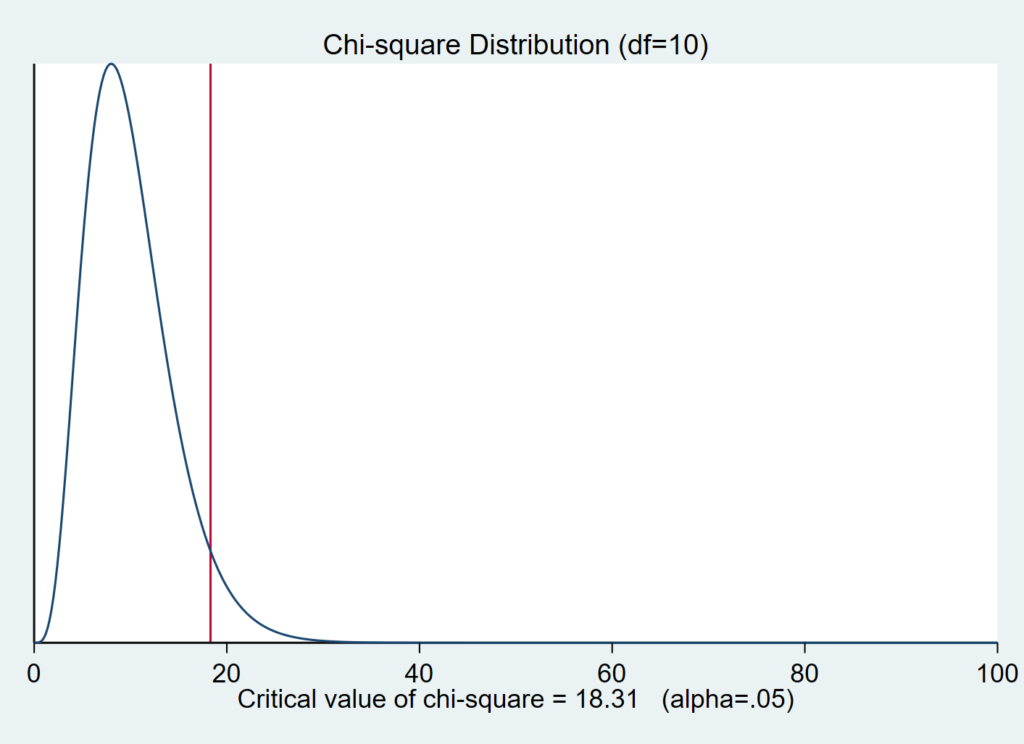
線より右側にいる確率を求めたいので、前述のように、

1 – χ2分布(自由度，χ2値)

で求められる、ということになります.

3．回帰モデルでの結果の取り出し

回帰モデルではさらに推定値、信頼区間、P値を、結果を表示したい変数すべてでlocal macroなど使って表現します.

ここで、linear regressionは結果がt分布に基づいており、logistic regressionやCox PH testは正規分布に基づいており、計算方法が異なります.

P = 2*(1 – T(df, |t|)) 　で与えられるため、Stataのコードとしては、

P = 2*ttail(df, abs(t))

となります.　ここで、t値は

t = _b[var]/_se[var]

です.

95％信頼区間は、推定値±t_α/2ですので、t分布においては、

invttail(df, α/2)

で与えられるため、

となります.

Logistic回帰やCox回帰モデルでは、t値の代わりにz値が同様に計算されますので、

P = 2*normal(-abs(z))

でP値が与えられ、

となります.

Local macroを用いて以下のように値を取り出すことができます.

１）線形回帰の場合

   .regress depvar var
	.local coef = _b[var]
	.local low = _b[var] - invt(e(df_r),0.975)*_se[var]
	.local low = _b[var] + invt(e(df_r),0.975)*_se[var]
	.local p =  2*ttail(e(df_r), abs(_b[var]/_se[var]))
	.display `coef', `low', `high', `p' 

sysuse auto, clear	 	 
  regress price trunk weight length foreign	 	 
  foreach v of varlist trunk weight length foreign {	 	 
	local coef`v' = _b[`v']	 	 
	local low`v' = _b[`v'] - invt(e(df_r), 0.975)*_se[`v']	 	 
	local high`v' = _b[`v'] + invt(e(df_r), 0.975)*_se[`v']	 	 
	local p`v' = 2*ttail(e(df_r), abs(_b[`v']/_se[`v']))	 	 
 	display "`v'", `coef`v'', `low`v'', `high`v'', `p`v''	 	 
  	}

さらに、表示するデータの桁数を指定する方法としては、

%4.2f、%4.3fなどをつければよく、

display "`v'", %4.2f `coef`v'', %4.2f `low`v'', %4.2f `high`v'', %4.3f `p`v'' 

２）Logistic regression、Cox PH testの場合

logistic foreign price trunk weight length 	 	 
foreach v of varlist price trunk weight length {	 	 
	local coef`v' = _b[`v']	 	 
	local low`v' = _b[`v'] - invnorm(0.975)*_se[`v']	 	 
	local high`v' = _b[`v'] + invnorm(0.975)*_se[`v']	 	 
	local p`v' = 2*normprob(-abs(_b[`v']/_se[`v']))	 	 
	display "`v'", %4.2f exp(`coef`v''), %4.2f exp(`low`v''), %4.2f exp(`high`v''), %4.3f `p`v''	 	 
	} 

4．まとめ