このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、前回に引き続き、スプラインをxblcコマンド抜きで描いてみよう!というテーマで、今回は生存時間分析によく使われるCox比例ハザードモデルに実装してみたいと思います.
xblcコマンドはオッズ比やハザード比といった「比」を計算するときに結構トリッキーなことをしてのけていたのですが、以下のような欠点がありました.
- 異なる2群で別々のRCSを引くときに、リファレンスを片側の群で設定することができない
- 多重補完後のデータで行うことができない
- やたらと時間がかかる
ハザード比でもオッズ比でも、リファレンスカテゴリを指定する必要があります。そして、指定したリファレンスカテゴリーの値で割り算することで、ハザード比やオッズ比が求められます.
点推定値だけならば話は簡単なのですが、信頼区間があるので、単純に割り算すればよいというわけではありません.
ハザード比やオッズ比の元となる、ハザードやオッズですが、それぞれexp()の中の線形予測子が線形回帰の式になっています.
リファレンスカテゴリのハザードやオッズで割り算する際は、線形予測式の中では引き算になります.
1.ハザード関数
初めに、ハザード比、というもので用いられる、「ハザード」ってなんでしょうか?これはすごく短い時間でイベントが起こる確率のこと、と理解しておきましょう.
もうちょっと正確に言うと、
時間tまで生存していた、という条件の下で、次の瞬間(t+Δt)までの間にイベントが起こる確率
となります.
Cox比例ハザードモデルというのは、ハザードの比を求めることを目的としています.
ロジスティック回帰では確率piのロジット(logit)、対数オッズ(log odds) が線形予測式で表現されるのでしたが、ハザードも線形予測式が組み込まれているので、基本は同じです.式にするとこんな感じ.

もう少し詳しく言うと、
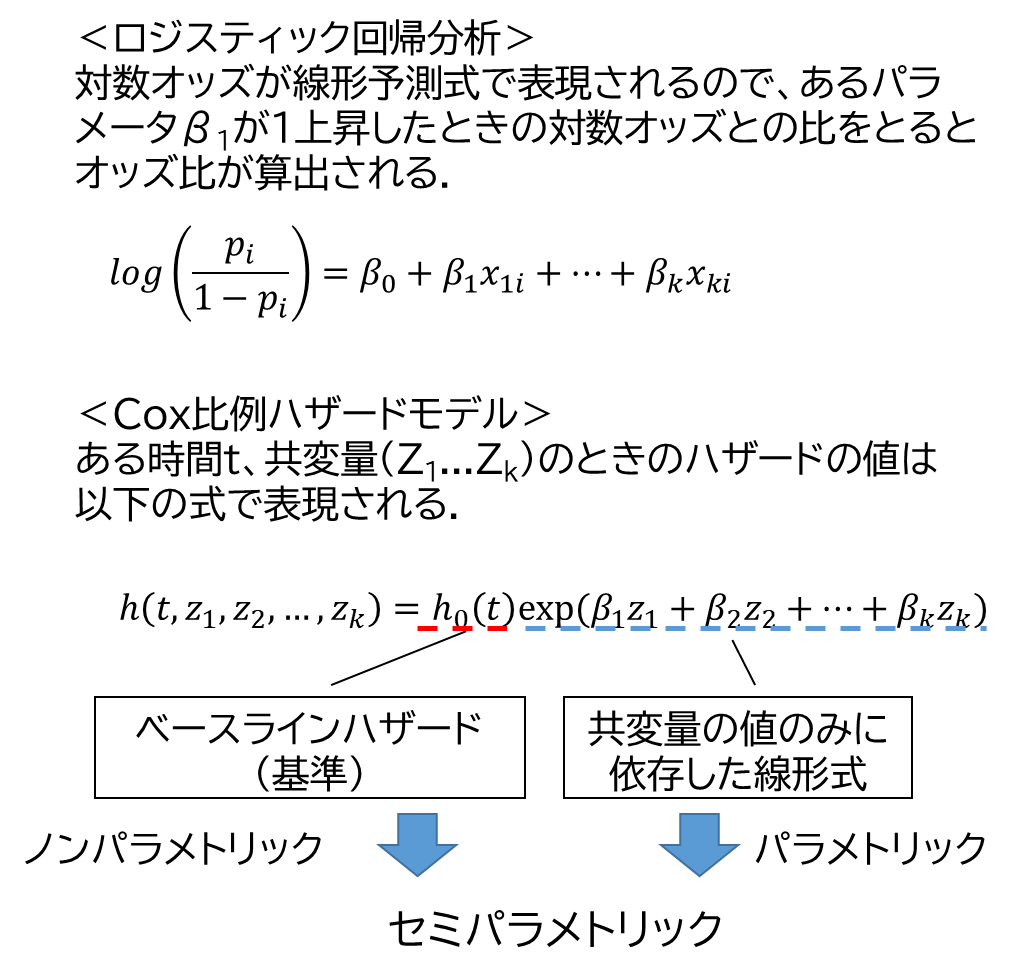
ここで少し気を付けたい、というか注目したいのは、β0、つまりy切片がない、というところでしょうか.
それと、線形式の頭にh0(t)というものがくっついていますが、時間tによってウネウネと変化するベースラインハザードになります(ノンパラメトリック).
線形式とノンパラメトリックなベースラインハザードを合わせて使うのでセミパラメトリックモデルと呼ばれるわけです.
共変量z2が1だけ変化したときにハザードがどれだけ変化するかを表したいときは次のようになります.

実際には対数ハザードを計算して最後にexponentして戻してやることになりますが、これはロジスティック回帰と同じですね.
2.スプラインでハザード比を表す
スプラインの場合も、ある曝露因子を連続的に変化させたときに、参照基準におけるハザードと比較して何倍になるのかを見ますので、基本的な考え方としては同じに考えればよいです.
mkspline rcs_idpvar = idpvar, cubic nknot(3)このように入れると、rcs_idpvar1とrcs_idpvar2という新しい変数が誕生します.
これはそのままでは解読不能なのですが、3次関数の曲線を描くためにいい感じに設定された変数だと思っておきましょう.
stset duration, failure(event==1)
stcox rcs_idpvar1 rcs_idpvar2 cov1 cov2…ロジスティック回帰の時と同様、残念ながらリファレンスを表現することができません.これをどのように解決するのかを考えてみます.
下の数式はx1をxaとxbの2つの変数に分けたところと考えてください.
リファレンスの位置の rcs_idpvar1, rcs_idpvar2の値はそれぞれxar, xbrとなります.
それをそれぞれxa, xbから引き算すればリファレンスの値を引いた対数ハザード比が出てくるはずです.
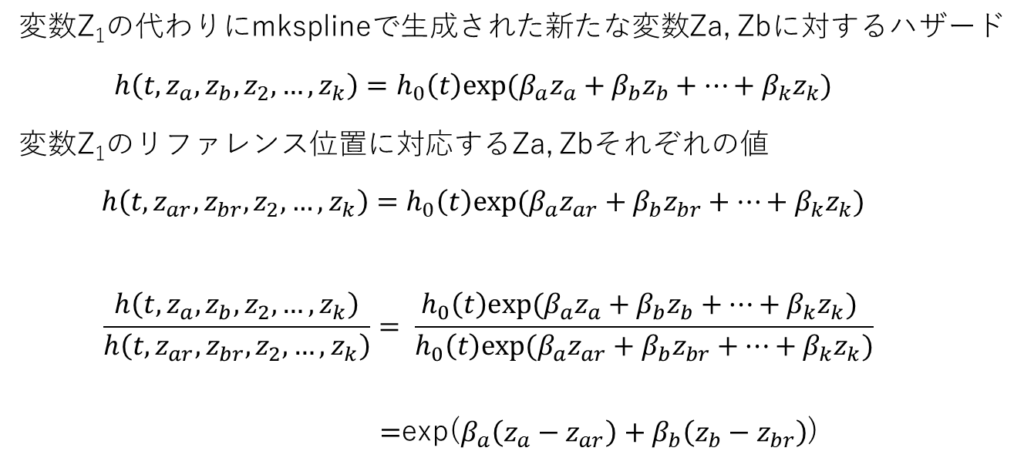
引き算した後のスプライン変数をrcs_idpvar1’ rcs_idpvar2’ などとして
係数はそのままにして説明変数 としてそのまま入れて計算させればハザード比がそれぞれ算出されるというわけです.
ここで、信頼区間付きでハザード比を求めるのにやはり”predictnl”を使うわけですが、この時に計算されるのは対数ハザード比になります.
なのでここまでの段階でリファレンスの引き算を行ってしまうのが楽です.
3.リファレンスカテゴリのスプライン変数を作成する
ここが今回の記事のメインになります.
手順としては次のように行います.
- テーブルの一番下に新しいダミーレコードを作成する
- ダミーレコードにおいて、RCSの横軸の変数Xがリファレンスとなる値を、その変数Xの中に代入する
- 変数Xがダミーレコードと同じ症例から、スプライン変数を取得する
- 新たに生成したスプライン変数を組み込んでCox比例ハザードモデルを実行
- predictnlで点推定値と信頼区間を得る
- グラフの作成
ここで、ある変数Xを横軸にして、3つのノットでリファレンスを10としてRCSを描くプログラムを作ってみましょう.上記の1~3のステップを示しています.(2022/1/27, 4/3に下記プログラムを訂正)
mkspline rcs_index = X, cubic nknot(3)
* add dummy observation for the reference
gen flag=1 if X== 10
sort flag
local NEW_OBS = _N + 1
set obs `NEW_OBS'
replace X = 10 in `NEW_OBS'
local rcs_ref1 = rcs_index1[1]
local rcs_ref2 = rcs_index2[1]
replace rcs_index1 = `rcs_ref1' in `NEW_OBS'
replace rcs_index2 = `rcs_ref2' in `NEW_OBS'
forvalue k = 1/2 {
local RCS_REF`k' = rcs_index`k'[_N]
disp `RCS_REF`k''
}
* comparing to the reference
forvalue k = 1/2{
local RCS_REF`k' = rcs_index`k'[_N]
replace rcs_index`k' = rcs_index`k' - `RCS_REF`k''
}
4. ハザード比を信頼区間付きで算出する
次に、ハザード比を信頼区間付きで算出する手順を説明していきます.
ここで便利な関数コマンド“predictnl”が出てきます.
Cox比例ハザードモデルでの解析を終えた後に、predictnlの関数を使えば対数ハザード比を信頼区間付きで計算してくれます.
predictnl yhat = predict(xb), ci(lb ub) level(95)(※lb=lower boundary, ub = upper boundaryのつもり)
あとはyhat, lb, ubをexponentすればOKです.
5.まとめ
ロジスティック回帰のときとはpredictnlに入れるための式が少し異なっていました.
しかしこちらのほうが理解しやすいですね.ロジスティックのときのほうが実は苦労しました.



コメント
いつも大変参考にさせていただいております。
質問なのですが、
mkspline X = rcs_index, cubic nknot(3)
のrcs_indexは何を指しますでしょうか。
例えば、血圧(変数:sbp)を横軸にした、予後(変数:event)とのCOX回帰のRCSのグラフを作成したいのですが、
グラフまでのコマンドを教えて頂けないでしょうか。
宜しくお願いいたします。
ご質問ありがとうございます。
rcs_indexというのは新しい変数名です。別にどんな名前でもかまわないです。
Xという変数から、ノットを3つにしてスプライン曲線がかけるように、新たな変数を作ります。
sbpという変数であれば、スプラインのための変数をsbp_indexとおくと、
mkspline sbp = sbp_index, cubic nknot(3)
という風にいれてみてください。あとはここに書かれているようなプログラムを追加していくだけです。
管理者様
早速のお返事いただき誠にありがとうございます。
私の勘違いでしたら、大変申し訳無いのですが、
mkspline sbp_index = sbp, cubic nknot(3)
で合ってますでしょうか?
mkspline sbp = sbp_index, cubic nknot(3)
ですと、variable sbp_index not found とでてきます。
失礼いたしました。それでできると思います。
今回のプログラムは煩雑ですので、まずはこちらからお試しいただくといいかと思います。https://statakahiro.com/restricted-cubic-splines%e3%82%92stata%e3%81%a7%e5%ae%9f%e8%a1%8c%e3%81%97%e3%81%a6%e3%81%bf%e3%82%8b
ありがとうございます。そちらも読ませていただき、作成できました。
多重代入後のHRをスプライン曲線で描きたいと思っております。
mi xeq: mi estimate を使用するタイミングを教えて頂けないでしょうか。
よろしくお願いいたします。
ご質問ありがとうございます。
mksplineのときにまずはmi xeq 0 を頭につける必要があります。
リファレンスのダミー症例を追加したりのところは不要です。
モデルを走らせるところは
mi estimate, post saving(dataset名) : stcox – – – – –
というのをやったあとに
mi predictnl b = predict(xb) using dataset名, ci(lb ub)
という風にしていただく必要があります。ここがComplete-case analysisとの一番大きな違いになります。
時間を見つけてこれも記事にしていこうかと思います。
ありがとうございます。
replace X = 10 in `NEW_OBS’
→これはRefを10と定義している という認識で良いでしょうか
gen flag=1 if X==0
→こちらの0という数字は何を意味しているのでしょうか。
大変失礼いたしました。0ではなく、10の間違いでした。
リファレンスを10に置いて、その値を下にコピーするためにフラグを立てます。
記事も訂正させていただきました。きちんと見ていただけると結構ミスがあるもので…。
これだけの記事を詳細にわかりやすく書いていただいていますので、、、仕方ないと思います。
ありがとうございました。本当に大変参考にさせていただいております。
いつも大変参考にさせていただいております。
内容に沿いTowayでグラフ化まで一通り実行できているのですが、手順の4.新たに生成したスプライン変数を組み込んでCox比例ハザードモデルを実行の部分で躓いております。stcoxの結果の推定値がプログラムを実行するたびに、異なるという現象が起きています。どうぞ、よろしくお願いいたします。
Coxモデルで推定値が再現できない、ということでしょうか?
リファレンスのところのスプライン変数の数値は特定できますか?その部分の値を引き算した値が新たなスプライン変数となるわけですが、
この値はいつも同じ値になりますか?共変量も同じ値になれば再現ができるはずですよね。
ありがとうございます。
disp `RCS_REF`k”の出力はいつでも同じ値です。こちらで設定したリファレンスの値とスプライン変数の数値が表示されるので、うまくいっているように見えます。
挙動が変だなと気になっている点は下記の部分です。
local NEW_OBS = _N + 1
set obs `NEW_OBS’
replace X = 10 in `NEW_OBS’
gen flag=1 if X== 10
sort flag
local rcs_ref1 = rcs_index1[1]
local rcs_ref2 = rcs_index2[1]
replace rcs_index1 = `rcs_ref1′ in `NEW_OBS’
replace rcs_index2 = `rcs_ref2′ in `NEW_OBS’
この部分は、ダミーレコードを作成して、リファレンスの値と対応するスプライン変数を新たに作成したダミーレコードに代入するという理解なのですが、このプログラムの順番だとsort flagでダミーレコードの位置が上側に上がってしまうので、最下のダミーではないレコードにリファレンスのスプライン変数の数値が上書きされる挙動になっているようです。毎回sortの結果で最下のレコードが変わるので、stcoxの結果が毎回変わるという現象につながっているように思います。flagの作成とsortの2行を先に実施するようにプログラムの順番を下記のように変えて試してみました。
gen flag=1 if X== 10
sort flag
local NEW_OBS = _N + 1
set obs `NEW_OBS’
replace X = 10 in `NEW_OBS’
local rcs_ref1 = rcs_index1[1]
local rcs_ref2 = rcs_index2[1]
replace rcs_index1 = `rcs_ref1′ in `NEW_OBS’
replace rcs_index2 = `rcs_ref2′ in `NEW_OBS’
これであれば、ダミーレコードは最下に居続けるので、ダミーレコードにリファレンスの値とスプライン変数が代入されることが確認できました。次の引き算も、リファレンスの値のレコードは0で、それ以外は引き算されています。最終的なリファレンスのyhatは0(exponentしてHRは1)になっているので、できたような気がします。
再現性も確認できました。
どうぞ、よろしくお願いいたします。
sortの位置でかわりましたね。ありがとうございます。データセットの構造がわかればこんな感じで修正が簡単にできますので、何かおかしいなと思ったときに中を覗いてみるのは大事ですよね。
記事も修正させていただきます。こんな感じで、ご覧になっている方からの建設的なフィードバックを頂けると助かります。今後もよろしくお願いいたします。
ありがとうございます。
多変量のCoxで実施する場合、ダミーレコードの共変量の値が空欄だとCoxのモデルから除外されると思うのですが、中心化処理を行う際の平均値をダミーレコードに代入する必要性はありますか?
また、多変量のCoxの解析後のpredictnlは、Xの値がこちらで設定したリファレンスの値でも他の共変量の値によっては対数ハザード比が異なるのでリファレンスが分からないグラフになってしまうように思いました。グラフ化をする際に中心化した値のデータに絞るなどの工夫が必要な気がするのですが、何か良い方法はありますか?
コメントありがとうございます。中心化に際してはダミーレコードは全く無視で大丈夫です。中心化する作業のときも無視されるので。
自分の場合は、ダミーはリファレンスを置く作業でのみ使うので、その後はIDが不在のレコードを消去する作業で消してしまっていますけどね。
グラフはすべての共変量を平均値に置き換える作業をしてから作成するので必ずリファレンスを通ることになると思います。
そうでなければプログラムのどこかでミスしたと考えます。