このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回のテーマは久々に統計学についてです。
ベイズの定理とか条件付き確率の話は、COVID⁻19の流行初期のPCRに関する考えについて述べた記事でも少し取り上げましたが、少しイメージしやすい形にまとめてみました。
1.数式での理解
高校生の時に条件付き確率を習ったときに狐につままれた気分になりました。
こんな問題見たことありませんか?
サイコロを振って偶数の目が出た場合に、それが4以上の目である確率は?
サイコロを振って偶数が出る確率が1/2で、4以上の数字が出る確率が1/2ですが、両方とも満たすのは、4と6だから1/3だ!
とかやってしまうと✖になるわけですが、最初のうち全く意味が不明でした.
何とかここは公式を覚えて乗り切ったのを覚えていますが、その式をイメージするのに苦労した覚えがあります.
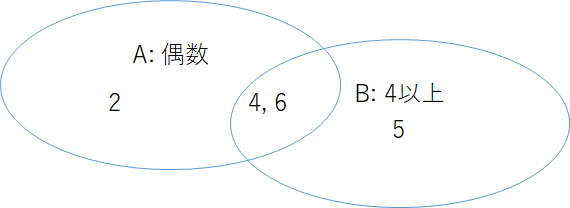
偶数であるという条件Aの確率P(A)は2,4,6のいずれかが出ればよいので1/2となります.
一方、4以上の目が出るという条件Bの確率P(B)についても、4,5,6のいずれかが出る確率ということで1/2です.
ここで条件A,B両方を満たす確率P(A∩B)は4,6のいずれかが出る1/3です.
ここから、公式を使って、
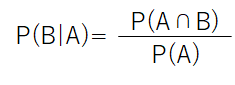
P(B|A)=1/3 ÷ 1/2 =2/3
と求まります.したがって、Aという条件下におけるBが生じる確率は2/3となるのです.
ここで、P(B|A)は、Probability of B given Aという言い方をし、条件付き確率はconditional probabilityです.
時は流れ、医学部に入学.そのころ(2000年代前半)ちょうどEBMの考え方が日本に広まり始めたかな、くらいの時期で、数学の話の中ではピンとこなかったこの条件付き確率にまた出会うことになります.
事前確率・事後確率と名を変えて出現してくれたおかげでようやくその意味を理解するようになりました.
ある疾患の有病割合が全国民の5000人に1人だとした場合、感度98%、特異度99%と謳われているスクリーニング検査が陽性であった場合に真の患者である確率を求めよ.
といった問題がそのものズバリの条件付き確率になります.
この場合、疾患の有病割合をP(A)とし、スクリーニング検査が陽性になる確率をP(B)としましょう.
疾患ありでしかもスクリーニング検査が陽性という確率はP(A∩B)です.
求めるのは、検査が陽性であるという条件(B)のもと、疾患あり(A)の確率は?という問いですので、P(A|B)を求める必要がありますので先ほどの公式から考えるとP(B)を求めないといけません.しかし残念ながらここではP(A)しかわかりません.
ここで、感度特異度から攻めていきましょう.
感度は疾患あり(A)、という条件のもと、検査が陽性になる(B)確率ですので、P(B|A)となります.ということで、先ほどの公式に当てはめると、
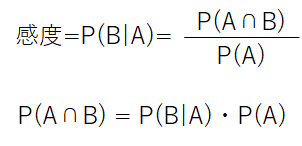
となりますので、P(A∩B)は一足先に求まりました.
さて、ここでP(B)をどうやって求めるのか、というのが残ってしまいましたが、これはあらゆる条件においても検査が陽性になる確率です.
つまり、ここでは疾患が本当にあろうが(A)なかろうが(A)とにかく検査が陽性になる確率を求めさせているので、AかつBとなるか、AかつBとなるしかないので、
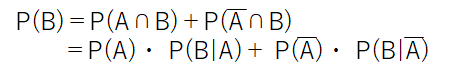
ここで、
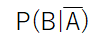
は、1-特異度ですので、求めるP(A|B)は

で得られることがわかります.う~む、数式だらけ…
2.2×2の表でイメージ
これをもう少しわかりやすくイメージするには、2×2の表を作ることが一番良いと思っています.
これまで数式を使っていかにも数学!という感じで解いてきましたが、いい加減頭が痛くなります.
そこで、下のような表をかいてみます.

小文字のa,b,c,dはそれぞれの条件を満たす人の人数が入るのですが、たいていは割合とか%ででてくるので合計10000人の表を作ると確実です.
Aは疾患有り無し、Bはスクリーニング検査陽性になるかどうかを表します.
求めたいのは、P(A|B)なのですが、これは、Bの条件を満たす集団のうち、Aを満たす人の割合を出せばいい、というただそれだけの話です.
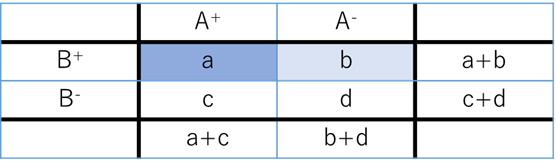
青い集団のうちの濃い青の人の割合を出す、というただそれだけの話です.
aの人数は、10000人×P(A∩B)となりますが、これは疾患ありの人に絞ったスクリーニング検査陽性と考えることができますので、
P(A∩B)=P(A)×P(B|A) …式①
右辺は二つとも既出の数値です.P(A)は有病割合、P(B|A)は疾患ありという人に限ったときの検査陽性の割合、つまり感度となります.
このとき、90度違う方向から表をみた計算も成り立ちますので、
P(A∩B)=P(B)×P(A|B) …式②
です.先ほどの式①と比べてAとBを逆にしただけです.これが成り立ってますよ~と言っているのがベイズ定理なのです.表を見れば一目瞭然ですよね.
求めるP(A|B)はP(A∩B)/P(B) で求められ、P(B) を頑張って計算すればいいことになります.aの数値は上の式①で出てきたそのままの値ですが、②をさらに進めると、bに入る数値を計算することになります.疾患がない人(1-P(A))の中で、検査が陽性になる確率(1-特異度)を計算したらよいので結局は先ほどの上のセクションの最後のところの計算をしていることになります.
3.具体例
先ほどの例ですが、5000人に1人しかり患していない病気であるなら、10000人集めてきても2人しか患者はいません.
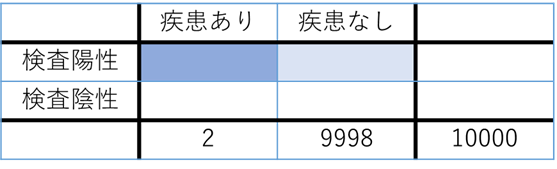
感度は100%に近いので、ここでは患者2人とも陽性になったとしましょう.
問題は疾患なしの人ですが、なしの人達でも100人に1人は間違って陽性になってしまうので、ここでは大体100人くらいいるとしましょう.
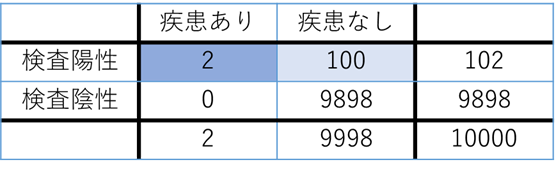
最終的には102人中2人しか真の患者ではなかったということになります.
ではこの102名に対して同じ感度、特異度の検査を繰り返したらどうなるでしょうか?1回目と2回目の検査は互いに独立しているものとして考えます.
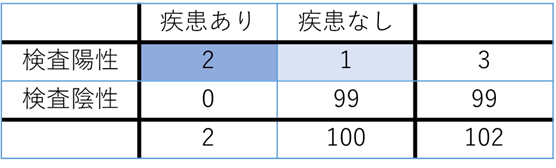
すると、今回は3人のうち2人が本物ということになり、かなり蓋然性が上がるのがわかります.
つまり、検査が陽性であっても、事前確率があまりにも低い場合にはもう一度陽性であることを確認するということが理にかなっていることがわかります.
4.イベントの原因に関する条件付き確率を求める
今度はイベントの有無に関して複数の要因がある場合に、イベントが生じた確率がある特定の原因によるもである確率を求める計算を考えてみましょう.
下の表のようにある特定のイベントOが生じるのに原因疾患が7つ想定されているとしましょう.
7つですべて説明できるとした場合、P(Di)の合計、すなわちΣP(Di)は1となります.
疾患Diが原因であった場合にOが生じる条件付確率が一番右のカラムになります.
このとき、イベントOが発生した患者において、疾患Bが原因であった確率はどうなるでしょうか?
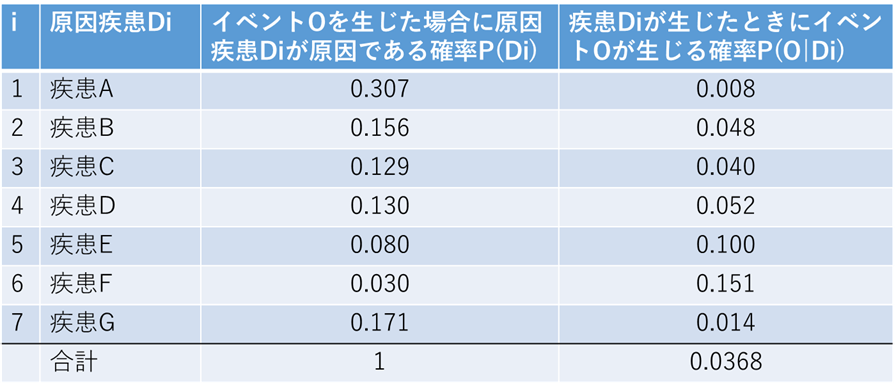
先ほどのクロス表とは考える向きが違うのですが、ひとまず、下のように考えてみてください.
各疾患に罹患している確率とその疾患にかかっている条件下でのイベント発生確率をかけたものがそれぞれの枠の中の確率になります.
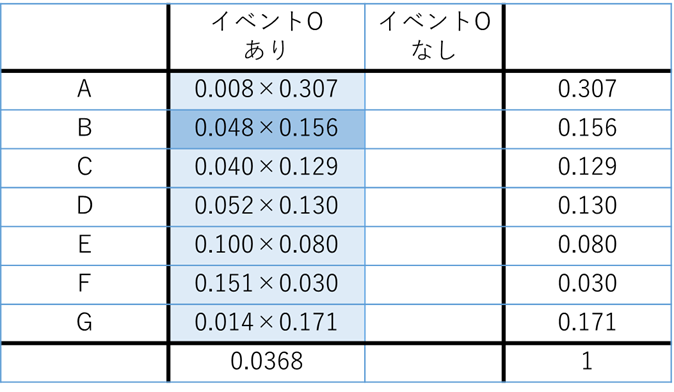
ということで、0.048×0.156÷0.0368=0.2035となります.
ここで、少し応用編ですが、上記の疾患のうちどれかに罹患する確率が0.01であった場合に、その集団の中で、疾患Eが原因でイベントOが発生する確率はどれだけでしょうか?
この表は、いずれかの疾患を起こした人の集計です.イベントフリーで病気にもならない、という人が100人中99人いる.そういう母集団の一部を切り取ってきたにすぎません.したがって元の母集団に戻すとしたら、一番右の列が合計で0.01となると考えればよいので、
0.080×0.01=0.0008 となります.
逆に、イベントOを生じた人の原因がEであった確率は?と問われれば、切り取ってきた集団だけで考えればよいので、0.1×0.080÷0.0368=0.2174 となります.
何らかの疾患にかかったのにも関わらずイベントを生じなかった確率は、この表の空いているところの確率となりますので、1-0.0368=0.9632 ですが、上記の疾患のうちどれかに罹患する確率が0.01の集団においては、1-0.0368×0.01=0.99963 となります.
まとめ
ベイズの定理はクロス表にまとめるのが一番手っ取り早いことがわかりました.
どうしても公式を使わないと解けない場面もあるのですが、その場合もクロス表を書いてから拡張するようにするとよいかもしれません.



コメント
以前、質問させていただいたものです。今回も宜しく御願いします。
コロナワクチンについての質問。
ファイザー社の治験
コロナワクチン接種者 21720人 プラシーボ接種者 21728人
累積発症者 8人(0.0004) 162人(0.0075)
未発症者 21712人(0.9996) 21566人(0.9925)
RR (8/21720)/(162/21728)=0.049(4.9%)
RRR 1-0.049=0.951(95.1%)
ARR 0.0075ー0.0004=0.0071
NNT 1/0.0071=140.8
このRRRが有効率95%の根拠になっていると思います。モデルナ社の治験、イスラエルのワクチン効果、
スコットランドのデータ等も同様に、RRRを重要視していますが、ARR,NNTのほうがもっと
重要視されなければいけないと思いますが如何でしょうか。RRRが同じでも縦軸のスケールが
違うとARRの差はかなりあり、NNTの差も大きくなると思いますが。どの論文も
RRRのみ重要視する根拠がわかりません、コロナ感染症の場合有病率が低いので尚更
気になりますが、間違っていればご教示ください。