事前確率から尤度比を使って事後確率を求める

新型コロナウイルスが国内で様々な混乱を引き起こしていますが、政治も医療もてんやわんやとなっています.

PCRの検出感度が高くないこと、8割は元気だけど重症化する人もそれなりにいて広まりやすいくせに診断しにくい、という困ったやつです.

PCRが保険診療内で実施できるような体制を整える、という官邸の発表を称賛する人もいれば、警鐘を鳴らす人もいます。

が、その２群の議論がしばしばかみ合っていないように思うのです.

PCRどんどんやろう！という人からは、感染防御策をどうするか、という意思決定に必要な情報を与えてくれる、というもっともな意見もあれば、もっと単純に、「とにかく検査で白黒つけたい」という意見も聞かれます.

PCRに慎重な人からは、軽症な人や「無症状だけど職場や学校から言われて…」という人まで検査したら貴重な医療リソースが枯渇してしまう、というような声や、陰性者の扱いが難しいなどの懸念がよくきかれるように思います.

しかし、議論がかみ合わない原因として、

両者の「P」がずれている

という要因が大きい気がします.

つまり、どのような集団を対象としていて、流行のどのフェースの話をしているのかを明らかにしないまま議論がかわされているように見えることがあるのです.

「PCRの適応」「学校の一斉休業」などには個人的には色々なことは思う一方で、ここでは疫学的な思考を以って、上記２群の考えのズレの正体を分析してみたいと思います.

1. 陽性・陰性尤度比を求めて検査前後の確率の変化を計算する
2. いろんな事前確率において事後確率がどう推移するのかをグラフ化する
3. おまけ（Stataでグラフ化）

というステップで解いていきます.

1．陽性・陰性尤度比から検査前後の確率の変化を計算

まず、以下の計算式を復習してみましょう.

陽性尤度比　＝　検査後オッズ　÷　検査前オッズ

オッズとは何かが生じる確率を生じない確率で割ったものです.つまり、

P　÷　(1-P)

で求められます.

検査後の確率をP(検査後)、検査前の確率をP(検査前)として、検査が陽性のときは陽性尤度比を用いるので、

P(検査後)　÷　（ 1ｰP(検査後)）

＝　陽性尤度比　×　 （　P(検査前)　÷　（ 1ｰP(検査前)） ）

これを変形すると、

P(検査後)　

＝ 陽性尤度比 × P(検査前) ÷ (（陽性尤度比 ｰ 1）× P(検査前) ＋1 )

検査が陰性のときには陰性尤度比を用いるだけです.

2. いろいろな事前確率において事後確率がどう推移するかグラフ化

コロナウイルスのPCRの感度や特異度は報告によってまちまちです.

だいたいいろいろなところの情報源を漁ってみると、感度30～70％、特異度は99％というところに収まりそうですので、感度を30％、50％、70％の場合に分け、特異度は99％で固定して検討してみることにします.

事前確率ですが、3/4の夕刊に「国内症例1000例超える」の文字が躍っていましたので、現時点で全国民を症状の有無や背景に関係なくランダムに検査した場合を一番下の事前確率とします.

日本では3/1の時点の厚生労働省の発表で1688件PCRを実施し、そのうち224件が陽性であり、13.3％の陽性率でした.

これから爆発的に患者が増えていき、有病割合が30％くらいまでの想定をしながらグラフ化してみることにしましょう.

特異度は99%で固定、 感度を30％、50％、70％の場合に分け てグラフ化してみます.

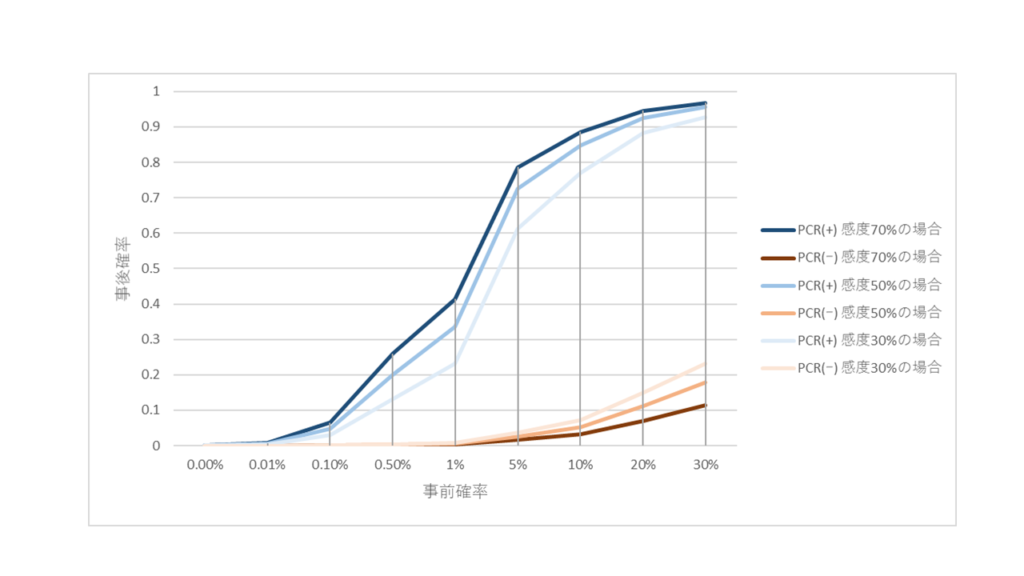
未だに流行が確認されていないような地域（グラフの左寄り）で、ランダムに検査してしまうと、仮に陽性とでてもその結果は信頼できない（10％も行かない）ものになりますし、逆に流行期においては検査が陰性であっても誤って疾患がないものとして分類されてしまう患者の割合が多くなってしまいます（グラフの右寄り）.

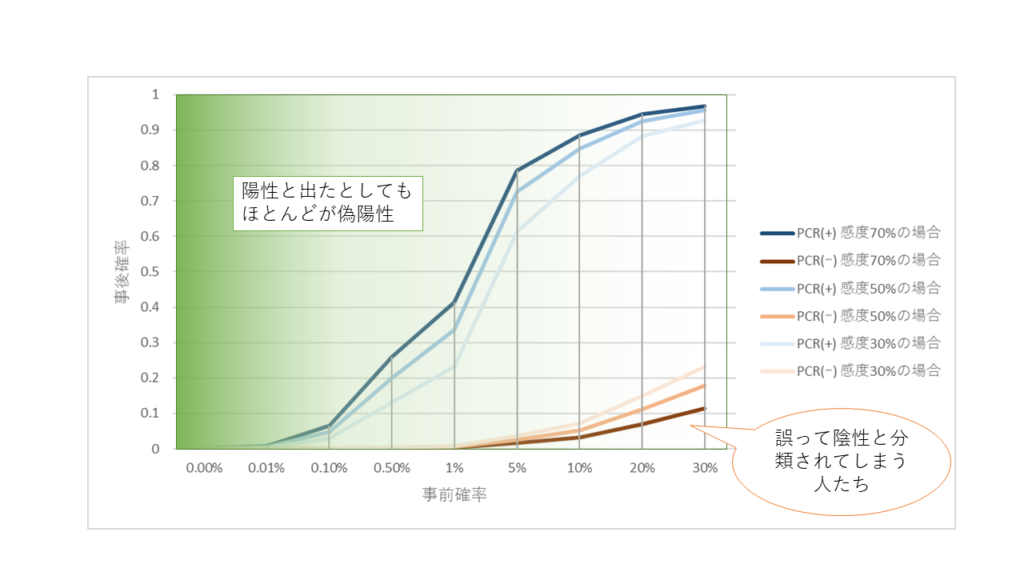
ということで、まとめると事前確率の低いときにはPCR陽性結果を鵜呑みにできないこと、流行期に入るとPCR陰性でも結構な割合で患者がいるということになります.

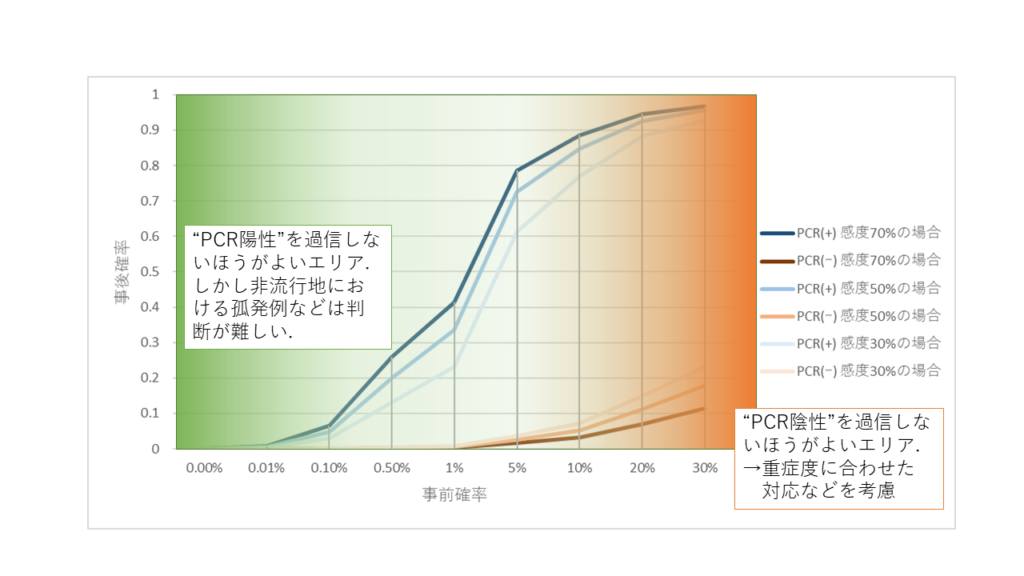
ここで、非流行地での孤発的な陽性例にどう対応するかが非常に問題になることが想像できると思います.

渡航歴や濃厚接触歴、呼吸器症状など、周辺的な情報をかき集めて事前確率を設定するしかないと思います.

濃厚接触歴がなく、呼吸器症状も乏しい、非流行地の患者さんが、職場からの求めでやってきた、という状況を想像していただくと、かなり左端に近い集団になりますので、PCRの結果が陽性でも陰性でも全くあてになりません.

逆に、入院患者や重症度の高い患者ではグラフの右寄りになっていくわけですが、たとえ事後確率がそれほど高くなくてもやはりPCR陽性例に対しては診断が正しい前提で進めるしかないでしょう.

また、流行期や、患者の状態によってはPCR陰性であっても陽性例と同じ対応をする、という判断が必要になる場合があります.

こうした患者背景も「どんな集団」であるかを見極めて検査結果の解釈をする上では重要な判断材料になります.

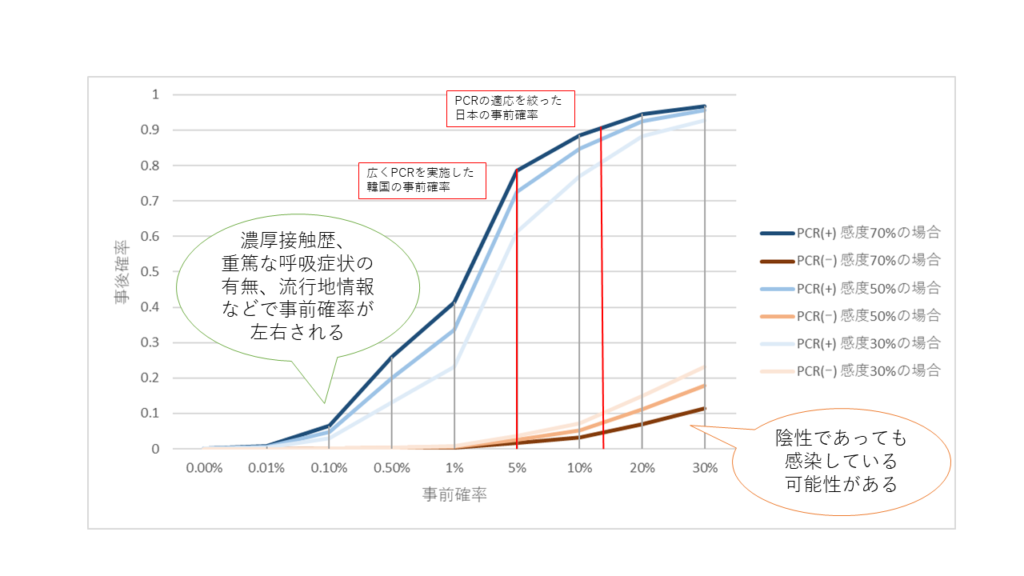
こうした前提があることを考えると、「どんな集団」を対象として「流行のいつの時点」での話をしているのかを明確にしないと同じ土台で話ができないのがお分かりいただけるでしょうか.

さらには日本中でウイルス感染自体が広まってきており、有病割合自体が右に徐々にシフトしてきているという点がありますので、今の時点がどうなのか、引き続き疫学的な情報を収集し続けることは重要であると言えます.

3．Stataでグラフ化

これまでのグラフはエクセルで作ってしまいましたが、このブログはStata縛り（？）にしていますので、Stataでグラフ化しておこうと思います.

clear
input pretest 
0.00001
0.0001
0.001
0.005
0.01
0.05
0.1
0.2
0.3
end

gen PLR70 = 0.7/(1-0.99)
gen NLR70 = (1-0.7)/0.99
gen PLR50 = 0.5/(1-0.99)
gen NLR50 = (1-0.5)/0.99
gen PLR30 = 0.3/(1-0.99)
gen NLR30 = (1-0.3)/0.99

gen posttest70pos = PLR70*pretest / ((PLR70-1)*pretest+1)
gen posttest70neg = NLR70*pretest / ((NLR70-1)*pretest+1)
gen posttest50pos = PLR50*pretest / ((PLR70-1)*pretest+1)
gen posttest50neg = NLR50*pretest / ((NLR70-1)*pretest+1)
gen posttest30pos = PLR30*pretest / ((PLR70-1)*pretest+1)
gen posttest30neg = NLR30*pretest / ((NLR70-1)*pretest+1) 
delimit;
twoway 
(scatter posttest70pos pretest, connect(l) lcolor(navy) mcolor(navy))
||
(scatter posttest70neg pretest, connect(l) lcolor(maroon) mcolor(maroon))
||
(scatter posttest50pos pretest, connect(l) lcolor(navy%50) mcolor(navy%50))
||
(scatter posttest50neg pretest, connect(l) lcolor(maroon%50) mcolor(maroon%50))
||
(scatter posttest30pos pretest, connect(l) lcolor(navy%30) mcolor(navy%30))
||
(scatter posttest30neg pretest, connect(l) lcolor(maroon%30) mcolor(maroon%30))
,
xscale(range(0.00001 0.3) log) 
xlabel(0.00001 "0.001%" 0.0001 "0.01%" 0.001 "0.1%" 0.01 "1%" 0.05 "5%" 0.1 "10%" 0.3 "30%")
legend(order(1 "PCR(+) 感度70%の場合" 2 "PCR(-) 感度70%の場合" 3 "PCR(+) 感度50%の場合" 4 "PCR(-) 感度50%の場合" 5 "PCR(+) 感度30%の場合" 6 "PCR(-) 感度30%の場合") pos(10) ring(0) col(1)) 
xtitle(Pretest probability) ytitle(Posttest Probability)     
;
delimit cr

線やマーカーの色は、”色の名前%数値”とすれば濃淡をつけることができます.

4．まとめ

検査の特性（感度・特異度）と疫学情報（有病割合）から事前事後の確率推移をグラフ化しました.

冒頭の話のかみ合わなさは、どの事前確率の人たちを対象にした話なのかが明確にならないままに議論されていることから生じているのではないか、と思うわけです.

事前確率は時間が経ては変化していきますので、そういった状況を予測しつつ対策を立てていく必要がある、ということを疫学的な側面から述べてみました.

何とか早く収束してほしいですね.