このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回は疫学ネタです.生存時間分析ではtime to eventがベースラインからイベント発現までの時間を表すことが一般的です.しかしこれは、ベースラインの効果がずっと持続することを前提としており、時間が経過する毎に変化するパラメータを特徴とするような曝露因子や共変量を考慮に入れていないモデルになります.
それに対して、時間依存性変数を用いる解析、時間平均化した変数を用いる解析は、longitudinalなパラメータの変化を考慮に入れることができるモデルになります.
今回はこれらのモデルの違い、使い分けについて具体的な論文をベースにして検討してみたいと思います.
1.3つのモデルの違いについて
3つのモデルの違いについて、その特徴を端的に記述している論文があります.日本透析学会が毎年行っている統計調査を元にCa, P, PTHなどと予後を解析した論文(Taniguchi, et al. Ther Apher Dial. 2013)に以下の様な記載があります.
“The baseline Cox model is appropriate for effects of baseline exposure, but does not reflect change of predictors during the observation period. The time-dependent model reflects alternation of parameters and is useful for examining comparatively short-term associations. Contrastingly, the time-average model is useful in examining long-term association between predictors and mortality.”
Ther Apher Dial. 2013より引用
もうちょっと自分なりにかみ砕いて解説をすると、
- Baseline model: 一番最初のベースラインの効果がどこまでも続くと仮定して、その効果を評価している.初診時に紹介状の内容や初期評価が予後をどれだけ予測できるのかを考えるのに役立つ情報を提供してくれる.
- Time-dependent model: 時間によって変化する曝露因子の短期効果を評価するモデル.毎回の外来受診や透析回診で結果を返すときに役立つ.
- Time-averaged model: 時間によって変化する曝露因子の、ある時点までの長期的な傾向がアウトカムにどう影響するかを評価するモデル.
ということになるかと思います.上記論文は疫学の土台がきちんとしている素晴らしい論文だと思います.
2.Time-dependent modelの例
ここでご紹介するのは、Kalantar-Zadeh K, et al. Kidney Int. 2006;70:771です.
維持透析患者におけるCa, P, PTHなどのCKD-MBD(CKD mineral and bone disorder)指標は、時間経過と共に常に変化します.従来のベースラインモデルだけではベースラインの状況しか解析に反映されません.
その曝露因子がずっと変わらない前提で解釈するならどのタイミングの値としても解釈できますが、実際にはそんなことはなく、毎回検査結果を患者さんに説明するたびに一喜一憂したりします.
この論文の研究はアメリカの大手透析グループである”DaVita”グループで、透析開始から3ヶ月以上経過した人のデータを使用した研究です.3-6ヶ月と導入したてだけどまずまず安定期に入ったかな、という人が40%ほどいるコホートになります.(日本の透析患者さんとちがって入れ替わりが激しいのがわかります…。)
Fixed covariate modelとtime-dependent modelに分けてCa、P、Ca*P積、PTH、ALP、paricalcitolのそれぞれアウトカム(2-year survival)に対する関係をみています.
Figureでそれぞれ違いを見せているので詳しくはPaperをご確認ください.
ただし、この方法においては注意点があります.それは、アウトカムが原因となって曝露因子や交絡因子が変化する可能性があるということです.
特にアウトカムに近くなればなるほどその傾向が増します.
例えば、リンが低いことが不良な予後と関係するのは、他の要因で衰弱して元気がなくなって食事がとれなくなったことに起因する場合、栄養状態やもっと言えば「食欲」そのものがこれらMBD指標の変化を介して不良な予後と関連しているように見えてしまう、ということです.
このような注意点についてはすでに別の総説でも述べられています.
時間と共に変化する共変量の扱いは、causal pathwayに乗った中間因子でもあり、交絡因子でもある、ということがしばしば起こりえます.そのような場合には単純にadjustするのではなく、周辺構造モデルなど別の方法を検討する必要がでてきます.
それと、Stataではtvc オプションを使って時間依存性変数の解析をすることが多いと思いますが、比例ハザード性の前提が崩れているときに対処する方法の中で紹介したものと混乱しがちなので注意してください.比例ハザード性が崩れているときに
stcox varlist, tvc(var) texp(ln(_t))とやるのは、time-dependent coefficients (time-varying coefficients)と呼んで区別します.
An Introduction to Survival Analysis Using Stata (third edition) の190ページにありますが、
It is useful conceptually to distinguish between time-varying covariates and time-varying coefficients, even though the latter can be estimated using the former. With time-varying covariates, the marginal effect remains the same but the variable changes, so the aggregate effect changes. With time-varying coefficients, the variable remains the same, but the marginal effect changes, so the aggregate effect still changes.
An Introduction to Survival Analysis Using Stata. Third Edition.
ということで、Coefficientは時間と共に変化するがあくまでもベースラインの値を使っているのがtime-varying coefficientsなのです.
ちなみにこちらの本は生存時間分析をStataで行う時に非常に参考になります.
3.Time-average modelの例
IgA腎症の研究で、time-averaged protenuriaと予後の関連をみています.
下図のような蛋白尿の経過を示した場合に、この推移線下面積を時間で割ることになります.台形の足し算になります.
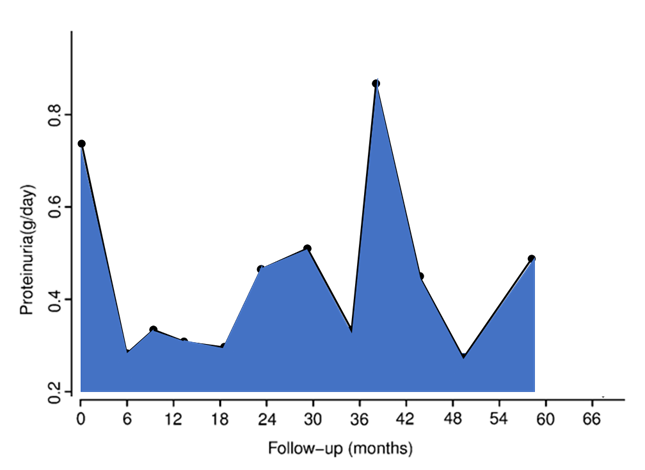
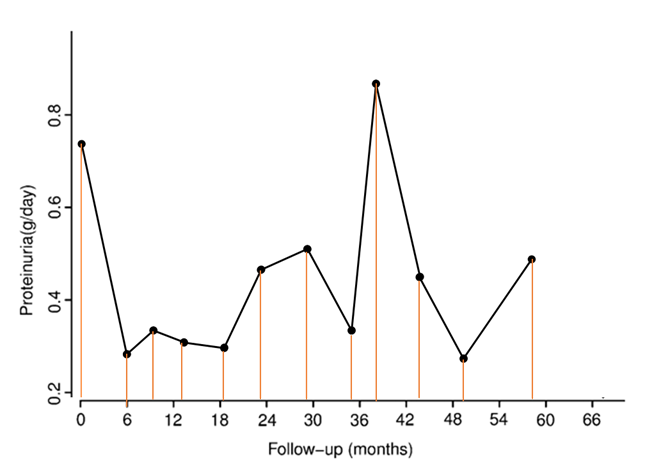
この計算は、隣り合ったオレンジの線を足して2で割り、その間の時間をかけたものをすべて足しあわせたものになります.言うのは簡単ですが、計算するとなるとちょっとややこしいですね.そんな計算にうってつけのコマンドがありましたので、サンプルデータを使って試してみましょう.使うコマンドは、”pkcollapse”というものです.
*** サンプルデータを展開
webuse pkdata, clear
*** ID番号1の人の32時間後までの血中濃度をプロットする
twoway connected conc1 time if id==1
*** 手計算したID番号1の人の台形公式による面積
disp .5*3.073403/2 + 0.5*(3.073403+5.188444)/2 + 0.5*(5.188444+5.898577)/2 + 0.5*(5.898577+5.096378)/2 + (5.096378+6.094085)/2 + (6.094085+5.158772)/2 + (5.158772+5.7065)*2/2 + 2*(5.7065+5.272467)/2 + 4*(5.272467+4.4576)/2 + 4*(4.4576+5.146423)/2 + 8*(5.146423+4.947427)/2 + 8*(4.947427+1.920421)/2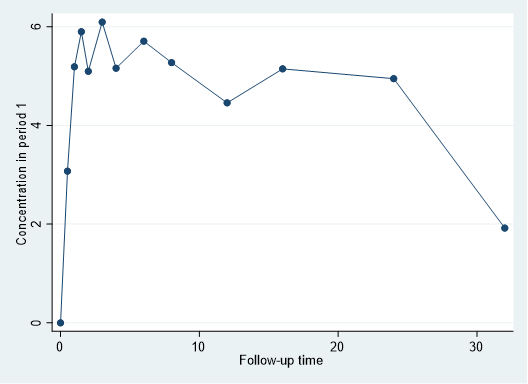
このpkcollapseは、デフォルトではスプライン曲線下面積を求めるようになっていますが、オプションでtrapezoidと入れることで台形公式で曲線下面積を求めることができます.
*** 台形公式による曲線下面積
pkcollapse time conc1 conc2, id(id) trapezoid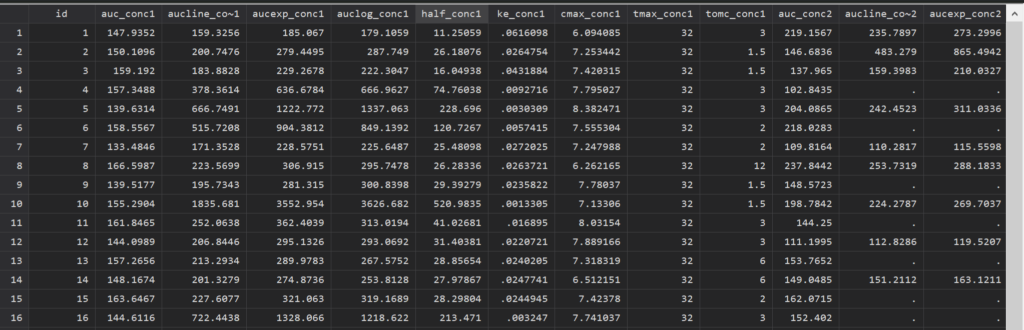
auc_conc1というのが台形公式で求めた、conc1濃度の曲線下面積になります.これを時間で割ります.例えば、ID 1の人は147.94が台形公式による曲線下面積で、時間にして32(時間?)かかっていますので、time-averaged valueは4.62となります.
さらにずーっと右の方にいくと、auc_conc2というのがあり、それがconc2濃度の台形公式で求めた曲線下面積となります.同様に32(時間?)で割ると、6.85となります.
このように、Longitudinalに収集したデータを1つのvariableとしてまとめることができるので、以後の解析には1つの変数として投入することができるため簡単に済ませることができます.より詳しく知りたい場合にはコチラを参照ください.
まとめ
ベースラインモデル、time-dependent model, time-averaged modelは使いどころが異なります.どの時点からみた曝露因子とアウトカムの関係なのか、しっかりと認識した上で論文を解釈する必要があると思います.



コメント