回帰分析をするときに、何となく変数を入れるだけではなく、データの特性をきちんと踏まえてモデルを組むことが大切です.
- 説明変数同士の関係を散布図や2×2 Tableで記述
- 説明変数と目的変数の関係も同様に記述
その他にも、連続変数や順序変数が説明変数である場合、目的変数に対してきちんと線形の関連をもつか.
こういったことも確認することが重要なのですが、今回の記事では、それを視覚的に確認するのによいコマンドをご紹介します.
1.lowess plot でスムーズな曲線を描く
.lowess commandは、locally weighted scatter plot smoothingの略だそうです. どういうことかというと、部分的に重み付けをした回帰分析を実行してグラフ化する、というものです.
もっと簡単に言えば、回帰分析における要因とアウトカムの関連をスムーズな曲線によってつなぐことができるので、あとは視覚的にOKかどうかを確認する、というものです.
結構な計算量を要求するようで、スペックの低いPCでは気をつけてね~と書いてあります.
.lowess depvar indepvar, option
で書いていくのですが、線形回帰とロジスティック回帰のどちらでも使えるので、線形性を確認する上ではそこそこ使えると思います.
webuse lowess1, clear
lowess h1 depth
Wet holeとdepthの関係をみるものらしいですが、図のように散布図に沿った形で曲線が引かれており、両変数の関係性を見て取ることができます.
これだったら線形回帰でも大丈夫かな、くらいの当たりをつけることはできそうですね.
ロジスティック回帰の結果を見たい場合には、オプションにlogitと入れるだけです.
sysuse auto, clear
lowess foreign mpg, logit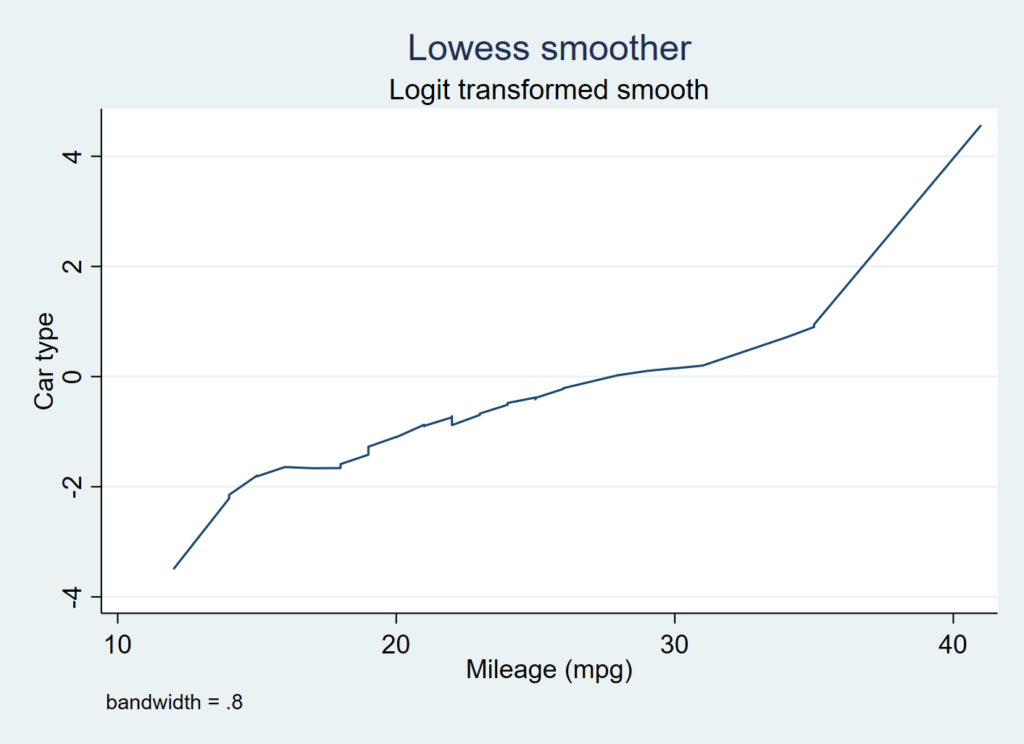
見た目でなんとなく直線的ならOKとするようです.
論文の中で使いたい場合にはもう少し綺麗に描きますよね.
また、Logit 0のところには何となく補助線を入れたくなります.そんなときは適宜、
sysuse auto, clear
lowess foreign mpg, logit yline(0)こんなふうにすればよいですし、ヒストグラムを重ねたければaddplotのオプションを使えば簡単です. ヒストグラムを少し透明にしないと折角のlowess plotが見えなくなってしまうので、
lowess foreign mpg, logit yline(0) ///
addplot(hist mpg, freq yaxis(2) bcolor(maroon%30)) ///
legend(order(2 "Lowess plot" 3 "Frequency")) ///
ytitle(Logit of Foreign car)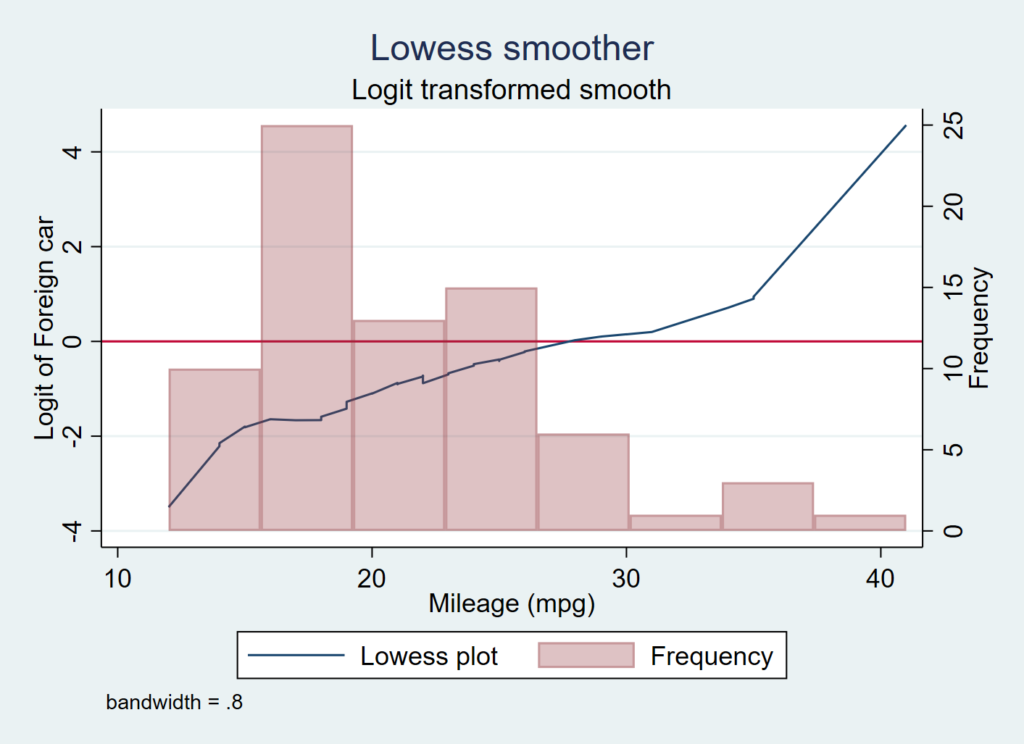
2.lincheckで4分位に分けてチェック
続いて、この連続変数をカテゴリー化したものを折れ線でつなぐ別のオプションを見てみます.
これは勝手に四分位にしてプロットしてくれる優れもので、なおかつ多変量モデルにも使えますので便利です. (lowessは単変量コマンドでした!)
方法としては、コマンドlincheckのあとに回帰式を書くだけ. 簡単ですね.
連続変数として、興味のあるexposureをアウトカムのすぐ後ろに書くことでグラフが生成されます.
sysuse auto, clear
lincheck logit foreign mpg
lincheck logit foreign mpg price weight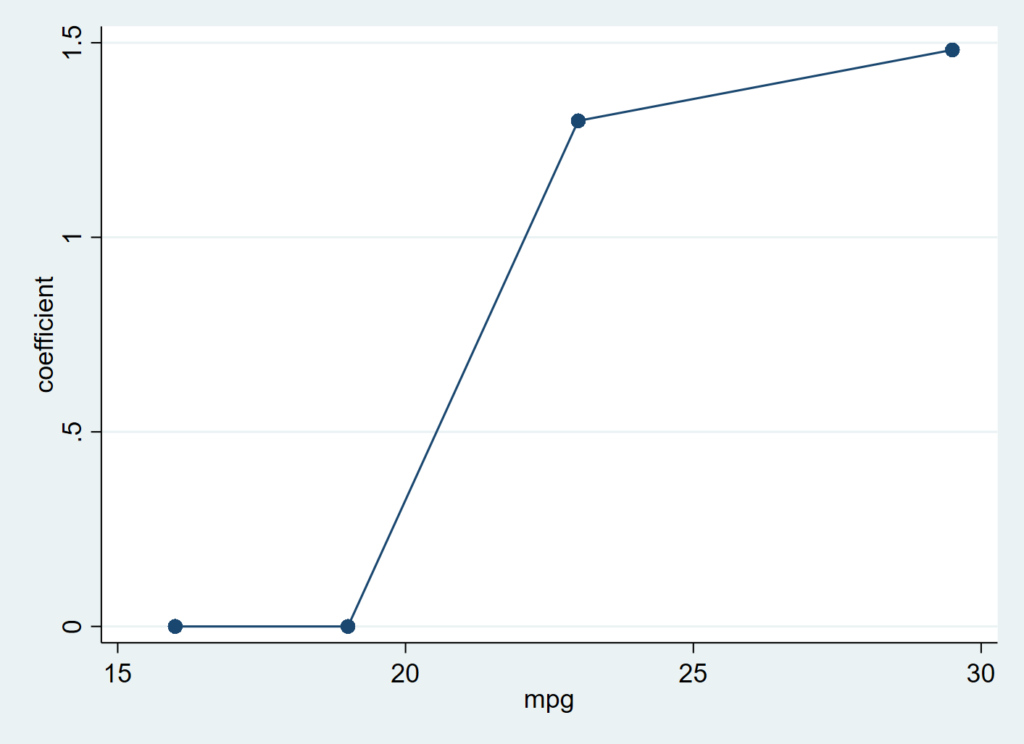
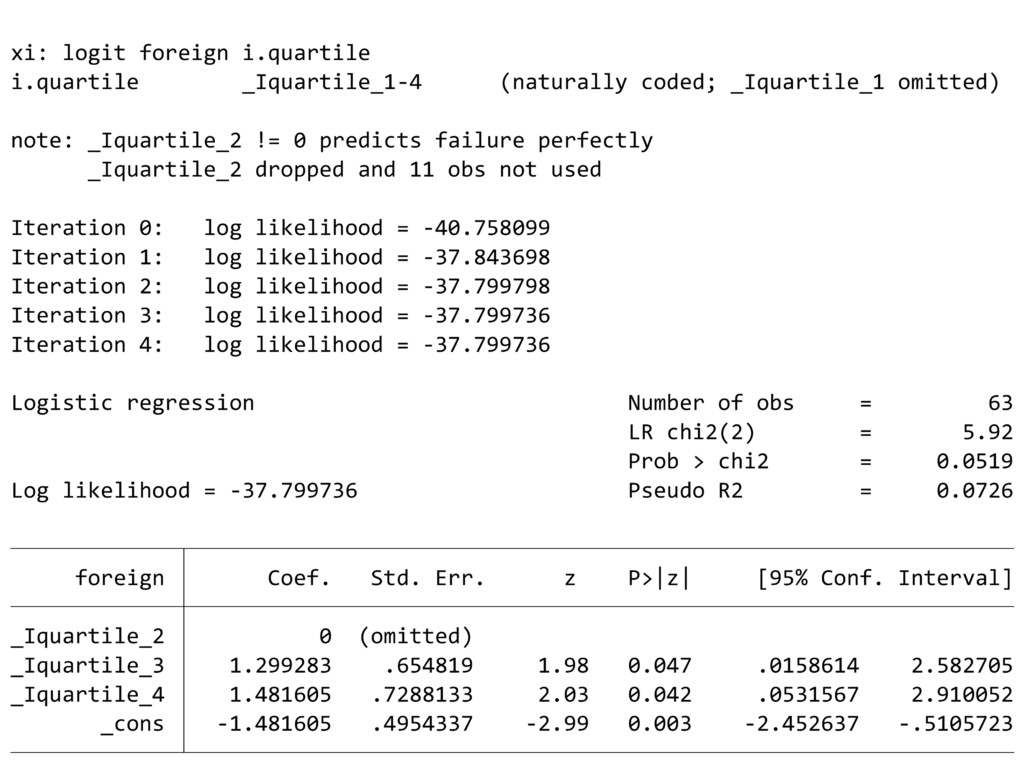
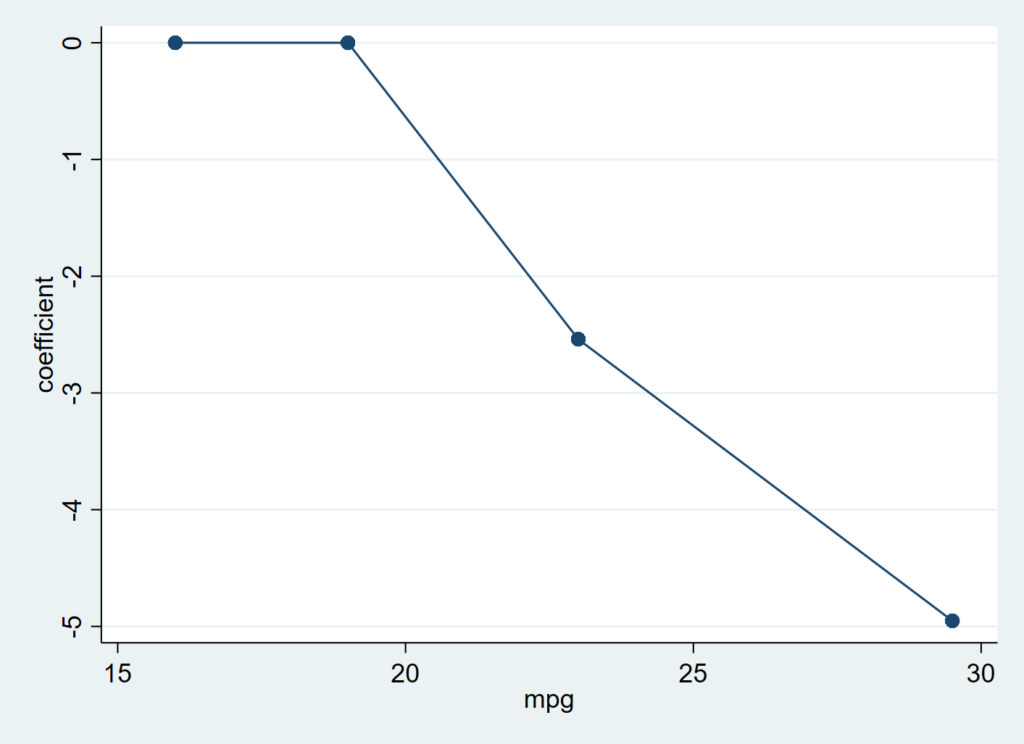
順序変数の場合にはやや複雑で、一度マニュアルでグループごとのlogitを作ってグラフにします。.ただしこれに関しては検定する方法もあります.
webuse fullauto, clear
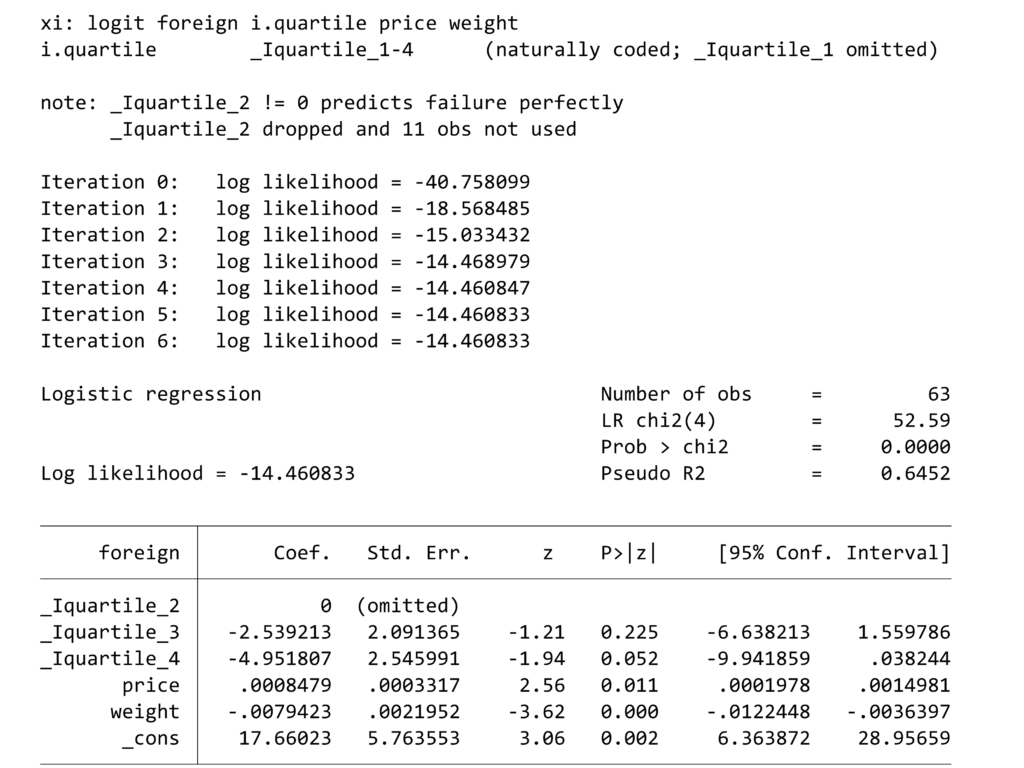
logistic foreign i.rep77
by rep77, sort: egen rep = mean(foreign)
gen logit = ln(rep/(1-rep))
twoway connected logit rep77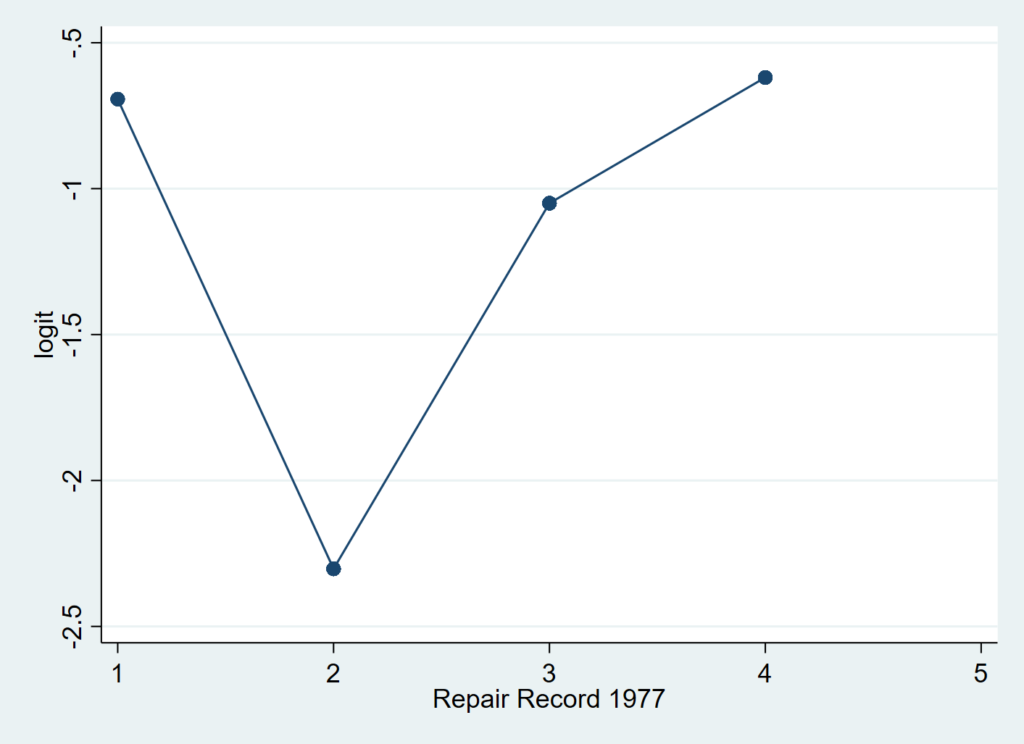
ただしこれに関しては検定する方法もあります.
webuse fullauto
tabodds foreign rep77これはトレンドのところのP値が<0.05ならば線形性は保たれている、としてよいようです. 実際に、この例では有意になっているので、図的な解釈とずれてしまいます.
3.fractional polynomialsで非線形の当てはめ
上記の方法で、連続変数でlinearity assumptionが怪しそうに見える場合、fractional polynomialsを試します.これは変数をべき乗変換して最適な形をさがす便利コマンドです.そのままでよいのか、二乗項にしたほうがよいのか、などです.
sysuse auto, clear
fp <mpg>: logistic foreign <mpg>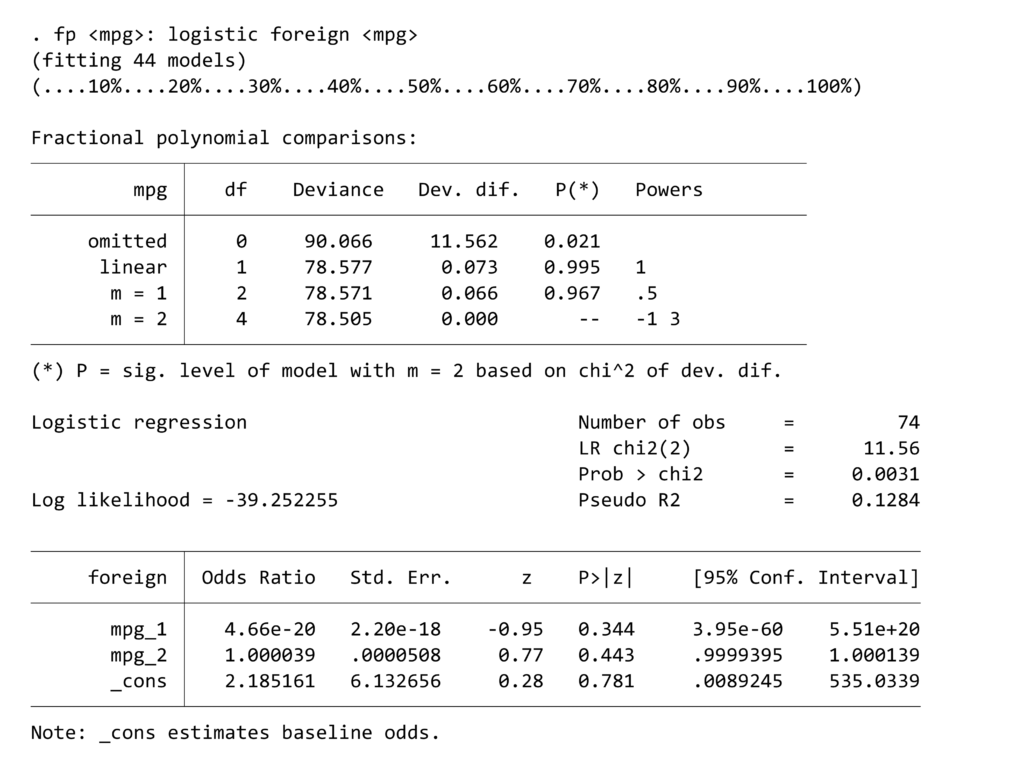
結果の解釈ですが、最も低いdevianceをもつ変換を選びます.P値は最適な変換スタイルとの差を示しています.
今回のケースではそのまま一次線形でよいのですが、power 0.5となっているところ(要は二分の一乗ですが)のほうがdevianceは小さいことになります.
しかしP値が有意ではないため、その差はない、と解釈され、最適な変換(変換しなくて済むならそれが一番いい)が選択されます.
これらの操作は説明モデルよりも予測モデルの構築に役立つのではないかと思います.
ちなみにfpですが、これも多変量モデルで行うことができるので便利です.
4.まとめ
今回は、連続変数や順序変数の回帰式における線形性について図的に検証する方法についてまとめました.論文の中に結果として出さないデータになることも多々ありますが、事前の検証を行う上で役に立ちそうな方法であると言えると思います.



コメント