「交互作用」というのは、ある要因と結果の間の関係が、サブグループによって異なるかことを指します.
薬剤Aの効果を見るとき、男女で分けると男性では8割に効いたのに対し、女性には2割しか効果がなかった、といった現象について統計学的に検証することができます. 交互作用を示すためには必要なサンプルサイズが大きくなることが知られていることも問題ですが、一番大きな問題は、直観的に理解するのが難しいことではないでしょうか?
Stataではvar1##var2というように書き、結果として出力された数値を理解しようとすると、いまいち理解しにくく感じる人も多いと思います。
そこで今回、ビジュアルに訴えるやり方で交互作用をどのように表現すればよいかについて説明していこうと思います.
1.交互作用とは
交互作用とは、サブグループ毎に要因と結果の関連性が異なることを示す疫学的な用語になります.
要因E(exposure)に対して結果O(Outcome)があり、その関係性を修飾するM(modifier)があって、以下のような関係性になっています.
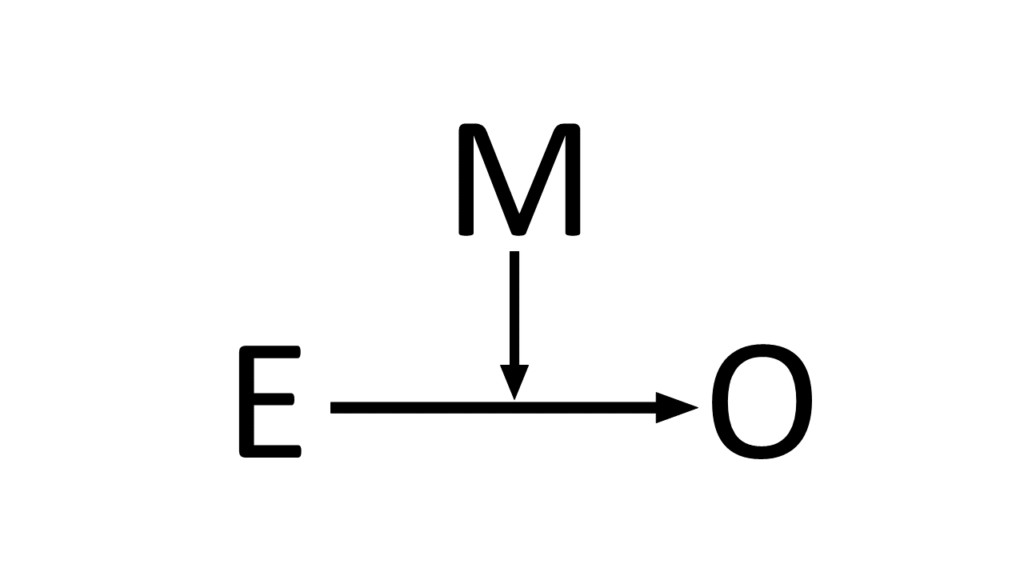
それはつまり、こういうことになります↓
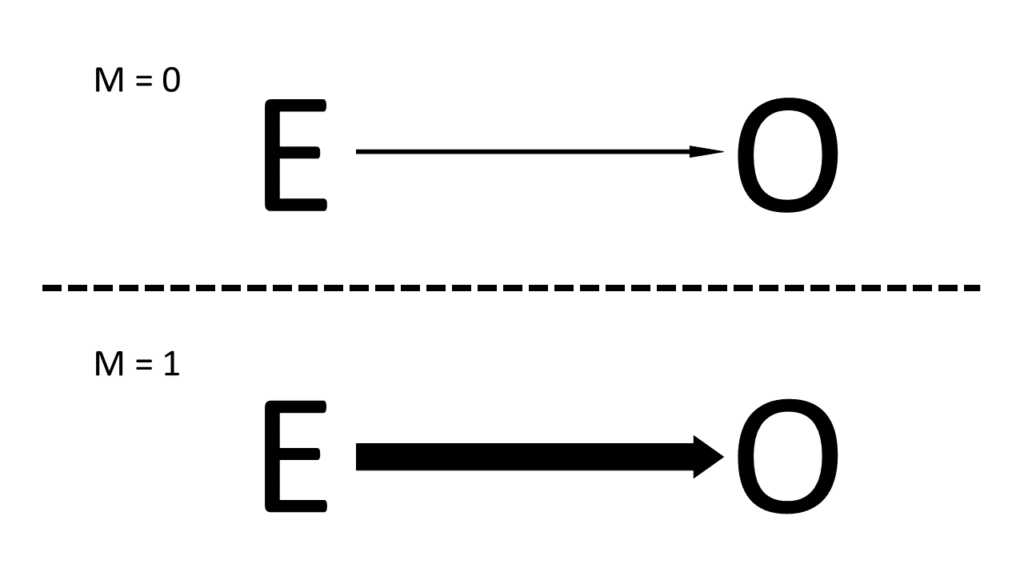
ここでは矢印の太さが関係性の強さを表すとします.
なので、M=1のときはEとOの関連はより強く、M=0のときは弱いということになります.
これを式で表すと、次の様になります.
O = β0 + β1*E + β2*M + β3*E*M
… Oはアウトカム、Eは要因、Mは修飾因子. E*Mを交互作用項という.
M=1 のときは
O = β0 + β2 + (β1 + β3)*E
M=0 のときは
O = β0 + β1*E
となることがわかります.
しかしこれはなかなか回帰式の結果として返ってきたときに直観的にはわかりにくいです.
そこで、図で理解することを考えることになります.
2.交互作用を図で表現する方法① Forest plot
前述のように、交互作用はサブグループ毎に要因と結果の関連性が異なることを示す方法なので、一番わかりやすくするならそのサブグループ毎に分けて記述することです.
要因E(exposure)、結果O(Outcome)、サブグループを表すM(modifier)1, M2, M3…とあるときに、
| サブグループ | 点推定値 | 信頼区間下限 | 信頼区間上限 | P | P for interaction |
| M1 | b1_0 | lb1_0 | up1_0 | p1_0 | px1 |
| b1_1 | lb1_1 | up1_1 | p1_1 | ||
| M2 | b2_0 | lb2_0 | up2_0 | p2_0 | px2 |
| b2_1 | lb2_1 | up2_1 | p2_1 | ||
| M3 | b3_0 | lb3_0 | up3_0 | p3_0 | px3 |
| b3_1 | lb3_1 | up3_1 | p3_1 | ||
| M4 | b4_0 | lb4_0 | up4_0 | p4_0 | px4 |
| b4_1 | lb4_1 | up4_1 | p4_1 | ||
| M5 | b5_0 | lb5_0 | up5_0 | p5_0 | px5 |
| b5_1 | lb5_1 | up5_1 | p5_1 |
一番最後のP for interactionが交互作用項の検定になります.
これだけでもだいぶわかりやすくなるのですが、
これを図に落とし込んだForest plotを描くとわかりやすいです.
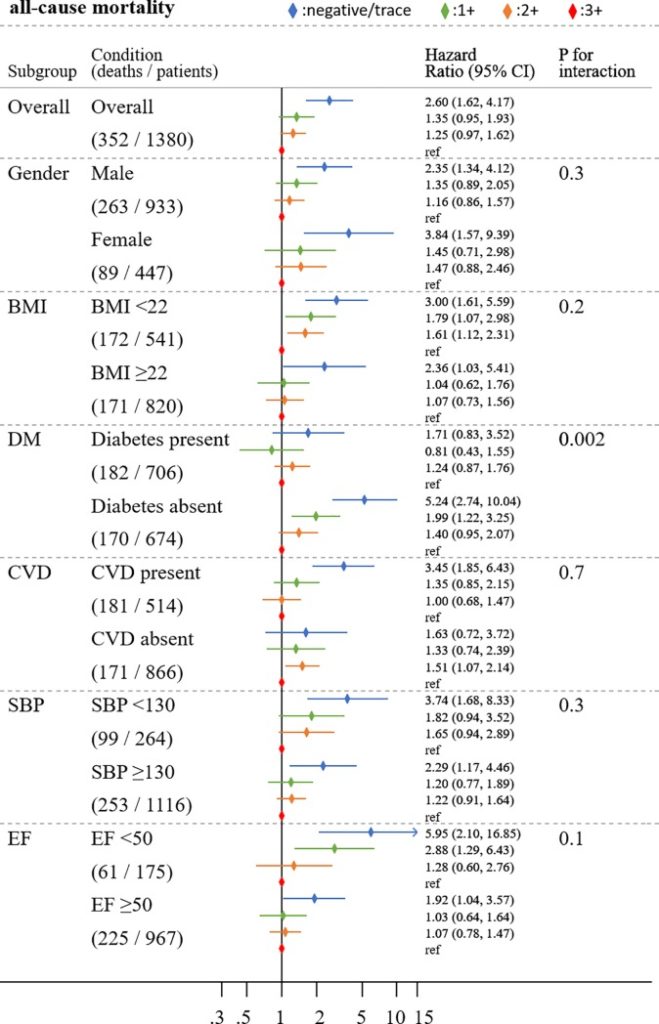
こんな感じで表現されます.
特定のグループにおいて特に曝露因子の影響が強いとか弱いとか、
あるいはどんな切り方をしても一貫性のある結果がある、ということを見せるのに最適です.
3.交互作用を図で表現する方法② Marginsplot
これはStata特有のコマンドですが、StataがStataたるゆえんというぐらい、便利なコマンドです.
これを使えば交互作用項を含んだ回帰式を走らせた後すぐに図で表現することができるのです.
“nhanes2″というデータセットを使用して実際にどんな風に見えるかを説明していきます.
webuse nhanes2, clear
regress bpsystol agegrp##sex
margins agegrp
marginsplot
/// まずは年齢ごとに収縮期血圧の予測平均値がどんな値になるかをプロット
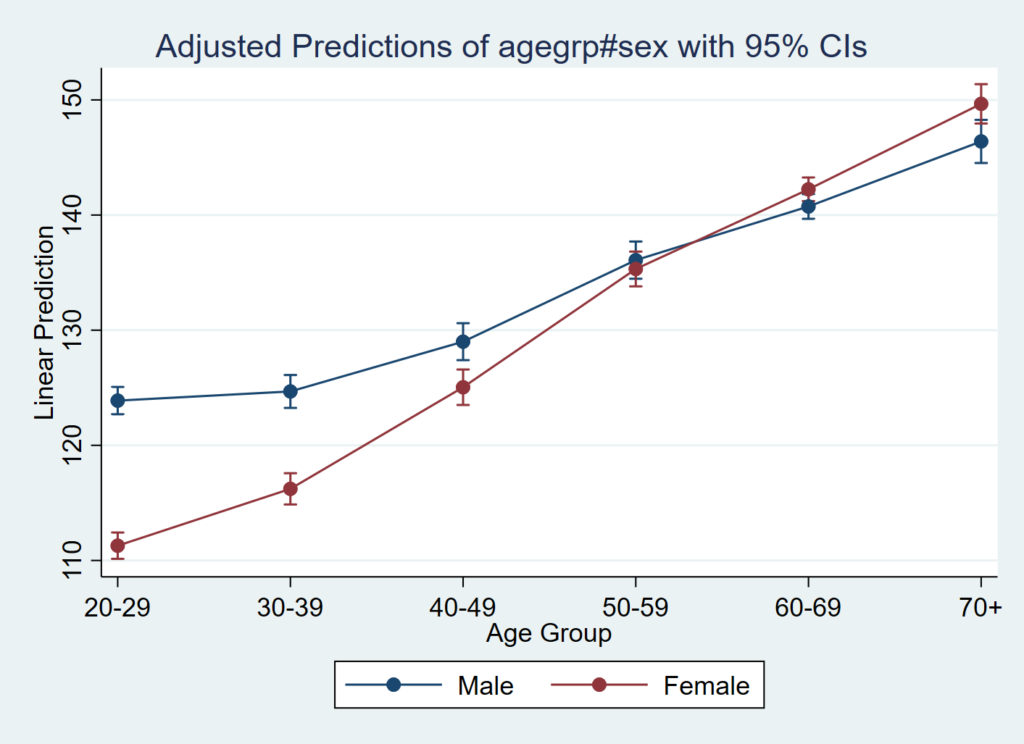
margins agegrp#sex
marginsplot
/// 次に男女ごとに収縮期血圧の予測平均値がどんな値になるかをプロットして比較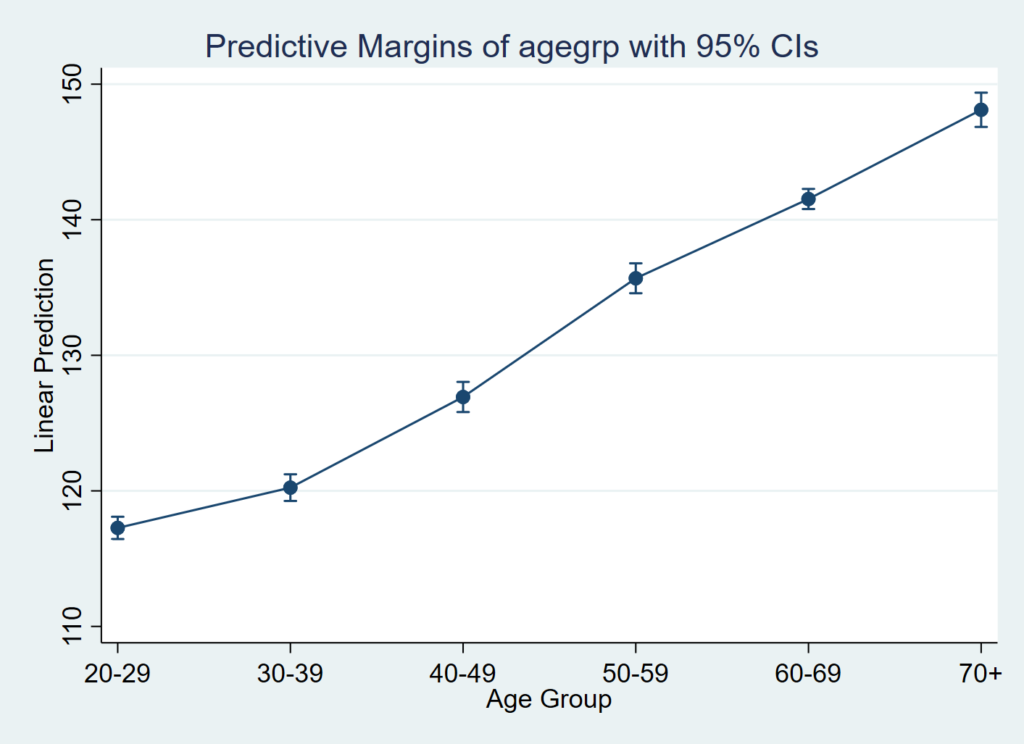
男女別でどう見えるかを表現すると、
4.交互作用を図で表現する方法③ RCS
さて、これまでは線形の関係における交互作用をみてきましたが、
RCSを使うと非線形の交互作用を見ることができます.
詳しい方法はLightstoneのWebsiteに載っています.
5.まとめ
交互作用を図的に理解する方法を解説しました.
このほかにも、非線形モデルとして、”mfpiplot”というコマンドもあります.adofileとして入手可能ですので、詳しくは解説をご覧ください.



コメント
[…] 以前、交互作用を示すための方法としていくつかご紹介した記事を書きました.この最後のほうでチラっとご紹介した、MFPIについて、今回改めてまとめてみました. […]