Restricted cubic splinesをStataで実行してみる

このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています．

Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています． ブログと合わせて個人の学習に役立てて貰えれば幸いです．

さて、今回は回帰分析の結果などをある1つの連続変数において非線形の関係であるときにその変化の具合を図的に表現できるRestricted cubic splines（RCS）をStataで実行するための方法を説明します.

下の図は4年ほど前、まだStataを使い始めて間もない頃にアクセプトされた論文ですが、ここではじめてRCSを使いました．はじめてRCSを見たときに、「自分でも描けるようになりたい！」と思って勉強したのでした．

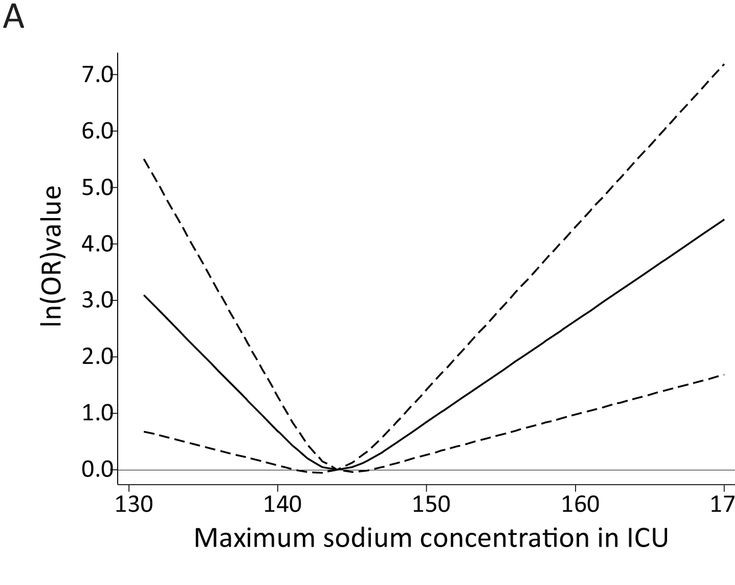
この論文では脳血管障害の人ではNaの値を下げないように気をつけよう、みたいなことを言われて実際どうなのかな、というのを思って調べたのでした．重症度で調整はしていますけど、それでも調整しきれない交絡の影響は否定できませんが．少なくとも図ではICU入室中のNa値の最大値が141～146くらいだといいよ、というもので、それを越えるようなNa値はやっぱりよくないという結論になったのでした．詳しくは論文を読んでみてください．（Open accessなので無料で読めますよ～）

今思えばちょっと殺風景で、もうちょっとおしゃれにできたなぁと思うのですが、それだけ自分が成長したということで！

今日はそのRCSをおしゃれに描く方法も説明したいと思います．

1．Restricted cubic splinesとは

二つの変数の関係を表す方法のデフォルトは線形回帰なのですが、その関係が非線形であるときに、三次関数までの式を区間ごとにあてはめて滑らかにつなげる方法がRCSです．このときに区間と区間のつなぎ目のことをknot(ノット、結び目)といい、決まった箇所で区切ることになっています．

k（ノット数）	パーセント点（ノット位置）
3	10, 50, 90
4	5, 35, 65, 95
5	5, 27.5, 50, 72.5, 95
6	5,  23,  41,  59,  77,  95
7	2.5, 18.33, 34.17, 50, 65.83, 81.67, 97.5

このときに変数の関係性を推定する方法はあくまで回帰モデルに拠っています．ちなみに一番外側の区間はサンプル数が少なくなることもあって、一次式が当てはめられますので、両端はまっすぐになります．また、信頼区間も広くなりますので、適当にtruncateするのがいいでしょう．

2．必要なコマンドのインストール

このRCSを描くためには、”xblc“というコマンドをインストールする必要があります．

.findit xblc

と打ち込むことででてくる

SJ-11-3 st0215_1 . Tab. and plot results after flex. modeling of quant. cov.
(help xblc if installed) . . . . . . . . . N. Orsini and S. Greenland
Q3/11 SJ 11(3):478
bug fix and added graph options for xblc

検索画面より

st0215_1をクリックしてado fileをインストールしてください．

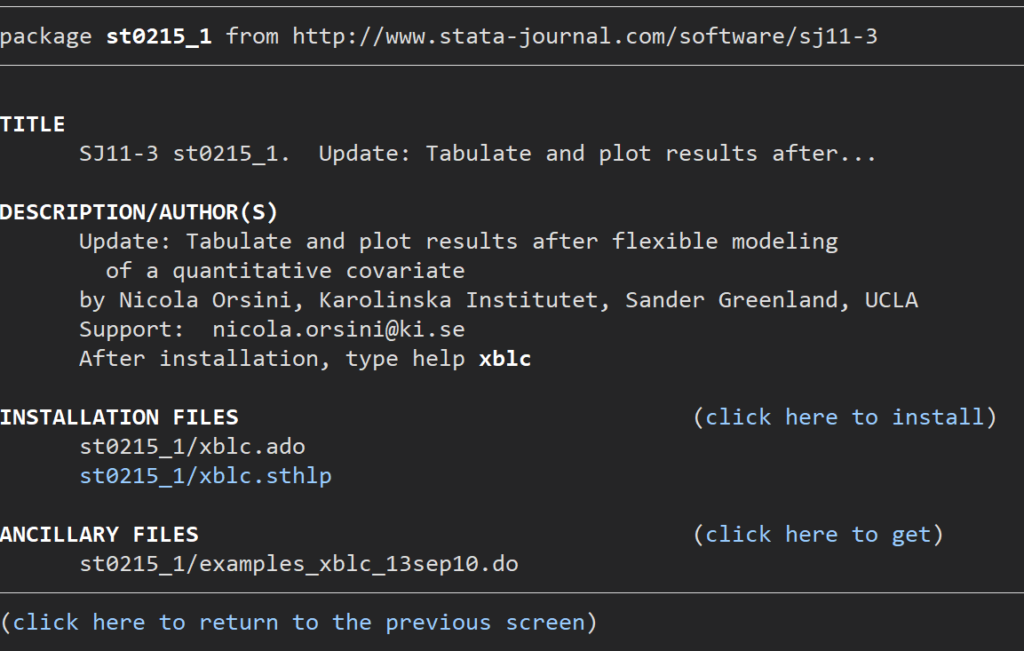
無事にインストールできたらHelp画面で中身を確認してみましょう．

xblc varlist, at(numlist) covname(varname) [reference(#) pr eform format(%fmt) level(#) equation(string) generate(newvar1 newvar2 newvar3 newvar4) scatter line twoway_options]

varlistのところには何らかの統計モデルを行って推定をしたあとに何らかの変形を施したものを入れます．これだけだと訳がわかりませんので、先にスプラインの区間を決めていくmksplineと回帰式を作ってこのコマンドにどうやってつなぐか、という順番で以後は説明して行きたいと思います．

3．区間を指定する”mkspline”

どの連続変数（oldvar）を横軸にして区間を指定するかを決めたらmkspline（もしくはmkspline2）コマンドで区切れ目を作ります．

新しい変数をstubnameと置いて次の様なsyntaxを書きます．

mkspline stubname = oldvar [if] [in] [weight] , cubic [nknots(#) knots(
numlist) displayknots]

knotの数をnknots(#)で指定するか、knots(numlist)に直接区切れ目の値を指定するかします．

cubicとすることでRCSのために三次関数の当てはめができるようになります．

そうすると、新たにstubname1, stubname2,…という変数ができます．（knotの数－１個）

当てはめたい回帰式にこれらを独立変数として入れることでスプラインを描くことができます．

.regress outcome stubname*

.logistic outcome stubname*

といった感じです．このときのアスタリスクはワイルドカードを意味します．つまり、stubname1, stubname2,…と言った感じです．似たような名前の変数が全部入ることになりますので、変数名の名付けはちょっと注意が要ります．

4．多変量解析、その後に変数の”中心化（centering）”

多変量解析は点推定値と信頼区間を求めますが、データセットのデータをすべて使うわけではないため、従属変数とknotを指定した独立変数以外の独立変数（交絡因子）を先に中心化しておく必要があります．

中心化するには、変数の平均値を引き算するだけですが、

sum indepvar
generate indepvar_c = indepvar - r(mean)
regress depvar stubname* indepvar_c

このように入れることで中心化が簡単にできます．また、その新しく作った変数を多変量解析に投入し、次の段階であるxblcを使ったスプラインの最終段階にいよいよ突入します．

5．”levelsof”で横軸の値を一括で取り扱い、”xblc”でグラフ準備

xblcでは、at()のところに横軸の値を指定してあげる必要があります．

xblc varlist, at(numlist) covname(varname) [reference(#) pr eform format(%fmt) level(#) equation(string) generate(newvar1 newvar2 newvar3 newvar4) scatter line twoway_options]

そのため、横軸の変数の値を一括して取り扱えるような方法が求められます．ここで登場するのが”levelsof“です．

.levelsof oldvar

としたあとに、r(levels) というマクロ変数に横軸の値がすべて格納されますので、

オプションat() には、at(`r(levels)’)としてDofileの中で実行すればOKです．

そして回帰式を前段階で実施したあとにいよいよxblcコマンドの実行です．

.xblc stubname*, at(`r(levels)’) covname(oldvar) line

とすればグラフが描かれます．

でもこのグラフはちょっと殺風景ですので、generate(newvar1 newvar2 newvar3 newvar4)の部分を使って点推定値と信頼区間を求め、それをtwowayのグラフコマンドで体裁を整えていきます．

6．Twowayで綺麗に

前項のgenerateオプションにある4つの新しい変数は、それぞれ①オリジナルの横軸の変数、②点推定値、③信頼区間の下限値、④信頼区間の上限値になります．

generate(newvar1 newvar2 newvar3 newvar4) specifies that the values of the original covariate, predictions or differences in predictions, and the lower and upper bounds of the confidence interval be saved in newvar1, newvar2, newvar3, and newvar4, respectively

xblc help画面より

これのいいところはグラフの色調を自分で自由に選べたり、あるいはヒストグラムなどと重ねたりすることができるという点です．

なお、ロジスティック回帰やCox回帰の場合にはリファレンスとなる値を指定したり、指数変換値に直す必要がありますので、オプションとして、reference(#) eformと付け加えることになります．

ということで、今だったらこんなグラフを描きたい！ということで掲載しておきます．

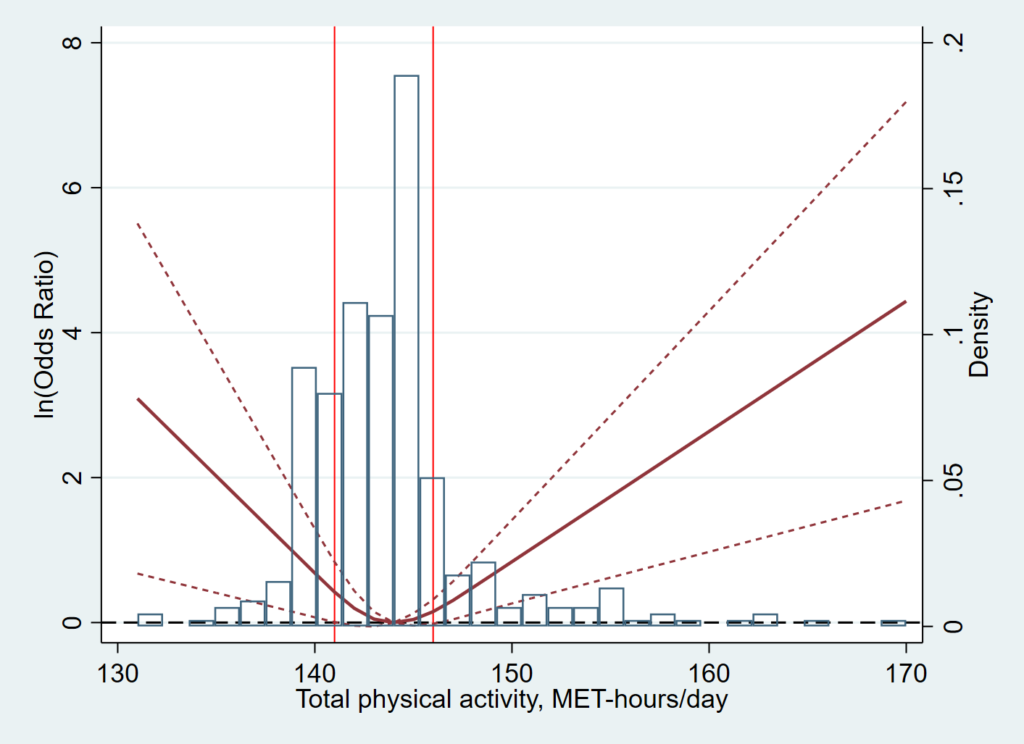
どうしても信頼区間が狭いためにイマイチだったりしますけど、これが限界のようです…

　

xblc maximum*, covname(maxna) at(`r(levels)') reference(144) line generate(pa or lb ub)	
#delimit;
twoway
	(line or pa, lc(maroon) lp(solid) lw(medthick) yline(0, lpattern(dash) lcolor(black)) sort yaxis(1)) ||
	(line lb pa, lw(medthick) lc(maroon) lp(shortdash) sort yaxis(1)) ||
	(line ub pa, lw(medthick) lc(maroon) lp(shortdash) sort yaxis(1)) ||
	(hist maxna, bin(30) fcolor(none) lcolor(edkblue) lw(medthin) yaxis(2)),
	ytitle("ln(Odds Ratio)") xtitle("Total physical activity, MET-hours/day") 
	legend(off) xline(141 146, lcolor(red) lw(thin))
	;
#delimit cr

7．まとめ

ということで、今回はRCSを綺麗に描く、という目標の下、Stepごとに説明していきました．最終的な流れをもう一度おさらいしてお開きにしたいと思います．

誰かのお役に立てればと思います．ご質問はFacebook group forumか本ブログコメント欄までどうぞ！