このブログでは、統計解析ソフトStataのプログラミングのTipsや便利コマンドを紹介しています.
Facebook groupでは、ちょっとした疑問や気づいたことなどを共有して貰うフォーラムになっています. ブログと合わせて個人の学習に役立てて貰えれば幸いです.
さて、今回は生存時間分析におけるサンプルサイズ設計について説明してみます.恐らく介入研究を企画しようという研究者にとっては研究計画段階で最もポピュラーな解析方法なのではないでしょうか.
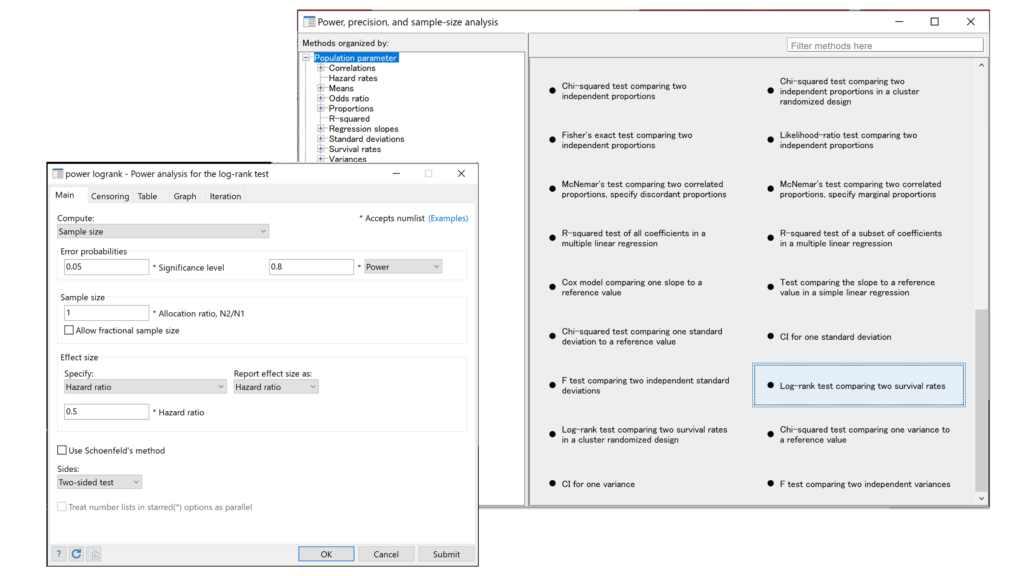
Power, precision, and sample size analysisをクリックしてみると、上記のような画面がでてきますが、Log-rank test comparing two survival ratesというところを見つけるだけでも結構一苦労ですね.しかしこちらのサイトをご覧になっているみなさんはきっとdialogue boxからいくことはせず、あくまでコマンドで書いていこうという気概の持ち主(?)だと思いますので、コマンドをご紹介していうことにします.
このセクションはPenn大の生物統計の授業とAn introduction to survival Analysis Using Stata 3rd ed.を参考にしています.
1.生存時間分析におけるサンプルサイズ設計の構成要素
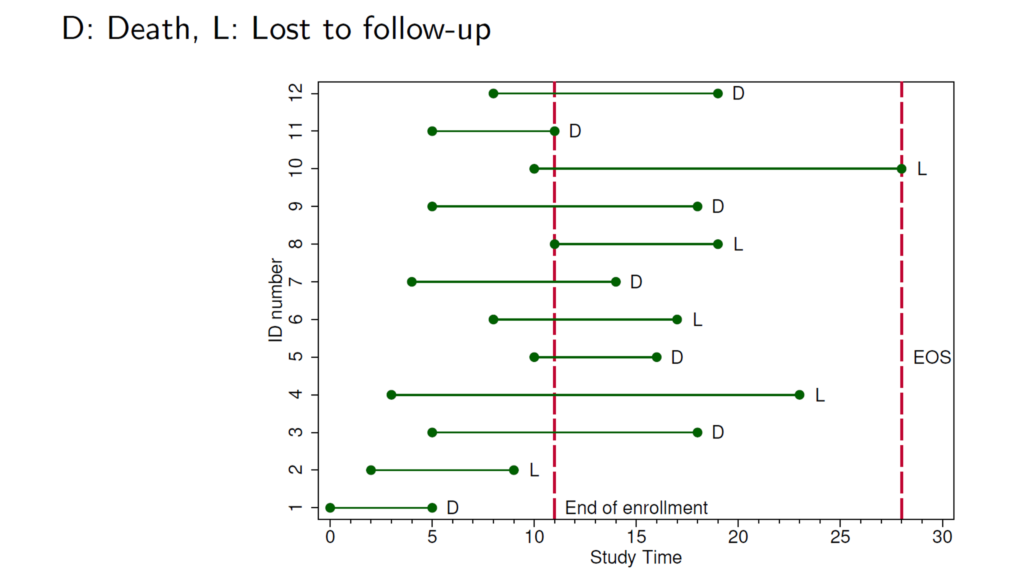
前向きの臨床試験(観察研究であれ介入研究であれ)では、実際の場面を想定すると下の図のように対象者がバラバラに組み入れられて、そして追跡されます.その時期は組み入れ時期とフォローアップ時期に分けることができますが、組み入れ時期にも幅があるということがポイントです.
そして治療群と対照群がどういった比率になっているか、どの程度の違いがあると「意味がある」と言えるのか、といったことを盛り込んで研究を行うことになります.
そしてさらに統計学的には第1種の過誤(一般的には5%)と検出力(80~90%)を設定することによってサンプルサイズを計算することになります.
これらをまとめると、
- 第1種の過誤の確率
- 検出力
- 効果の大きさ・程度(研究でdetectしたいと思っている程度)
- 介入 vs. 対照の比
が必要ということになります.
このうち効果の大きさはどのように評価するのでしょうか.それには以下のようなものがあります.
- 時点t における生存関数S(t) の差
- 生存関数S(t) のOverall の差
- median survival timeの差
- ハザード関数の差
- ハザード比
効果の大きさは最も小さな臨床的に有意義な治療・介入の効果を表します.ハザード比を使うことが多いです.
治療介入群とコントロール群の比は1:1を一般的に使いますが、治療群があまり集められず、対照群との比を1:1以上にする必要があることがあります.主には倫理的な問題、治療介入が高コストであるなどの問題から決まります.サンプル数を最小にするには両群のイベント数が同じだとよいようです(Kalish and Harrington, 1988).
そのほか重要な要素としては組み入れ期間(accrual period)と脱落です.組み入れ期間には順当に対象者が入っていくことを想定しています.しかしこれには色々とバリエーションはありそうです.
そして実際の研究には脱落というのが一定程度生じてしまいますが、それも最初の段階である程度見越したうえでサンプル設計をする必要があります.
2.Stataで用いられるコマンドstpowerとサブコマンド
Stataで活用できるサンプルサイズ計算のコマンドはstpowerというもので、さらにこれには3つのサブコマンドがあります.
1) stpower logrank
デフォールトではFreedmanの方法というものに基づいていますが、Schoenfeld法にすることもできます.両者は計算方法の違いだけなのですが、後者のほうがより少ないサンプル数で済むようです.
このサブコマンドの直後に、オプションでハザード比だけを書くと必要なイベント数だけがわかるにすぎません.実際にリクルートするのに必要な対象者数を計算するには、ある時点の対照群の生存確率を置いてオプションでハザード比を書くか、対照群と治療群の生存確率を書くかする必要があります.
stpower logrank, hratio(0.6) power(0.9) schoenfeld /* これだとイベント数しかわからない */
stpower logrank 0.3, hratio(0.6) power(0.9) schoenfeld /* 対照群の生存割合0.3、を入れると必要な対象者数が計算される */
stpower logrank 0.3 0.486, power(0.9) schoenfeld /* 0.3の0.6乗を計算すると0.4855...となるのでそれを治療群の生存割合と見積もれる */ 2) stpower exponential
こちらはexponential distributionを仮定したパラメトリックモデルの生存関数です.Log-rankは生のカプランマイヤーを比較していますし、Cox回帰はセミパラメトリックモデルといって、ベースラインハザードの形は生もの、それに連なる線形予測子の相対的な関係をみています.いわばハイブリッド型.アンドロイドみたいなかんじですかね.
これに対してexponential distributionを仮定したこちらは、数学的に完璧に式で表現できるので、扱いが簡単です.
stpower logrankで一定の時間における生存割合が少なくとも一つの群え必要だったのですが、exponentialの方ではhazard rateを入れてあげる必要になります.ハザード比を入れるのは両方共通です.
ここでオプションloghazardと入れることでlog-hazard difference testを行うことができます.デフォルトではhazard-difference testという保守的な方法で行っているのに対し、log-hazard difference testであればで必要なサンプルサイズを減らせるんだそうです.
stpower exponential 0.03, hratio(0.6) power(0.9) /* これだけでも必要な対象者数がわかる */
stpower exponential 0.03, hratio(0.6) power(0.9) loghazard /* デフォルトと異なり、log-hazard difference testを行うことで必要なサンプルサイズを減らせる */ 3) stpower cox
stpower logrank ではbinaryな変数にのみ使えたのに対し、coxは連続変数でも大丈夫です.
3.Follow-up期間とaccrual期間の設定
冒頭のところでも述べた通り、組み入れ期間には順当に対象者が入っていくことを想定しています.しかし、ちょっと想像してみるとわかると思いますが、組み入れの早い段階でたくさんエントリーすればするほど観察期間が伸びるので検出力が増しそうです.
これを加味して計算するにはexponentialが適しています.logrankのほうではsimpsonというオプションでminimum followup timeにおける生存確率、全フォロー期間終了時における生存確率、そして両者の中間地点での生存確率を生存曲線から拾ってきて入れる必要があります.
対してexponentialのほうでは、オプションでaperiod()でaccrual periodをどれだけにし、fperiod()で残りの観察期間を指定し、さらにaptime()でどれだけの期間で50%の人をリクルートするかを入れて計算ができます.
stpower exponential 0.03, hratio(0.6) power(0.9) fperiod(24) aperiod(12) /* 研究期間の最初の1年で組み入れて、その後2年フォローアップ */
stpower exponential 0.03, hratio(0.6) power(0.9) fperiod(24) aperiod(12) aptime(0.25) /* 最初の25%の期間で対象者を半分集める */ ※aptimeを使うときはloghazardオプションをつけることができませんので注意が必要です.
これで研究のためのリソースを前半に固めて対象者を早めに集め、効率を最大化しよう、という作戦が取れます.必要なサンプル数がどれだけ増減するかと、リクルートのために最初にどれだけコストがかかるかを天秤にかける際に使えるデータとなります.
4.まとめ
生存時間分析をベースとしたサンプルサイズ計算の仕方を説明しました.3つのサブコマンドそれぞれの特性を理解して、どれをあてはめるかを考えてみましょう.



コメント